Навигация
Методи розв'язування задачі
1.2 Методи розв'язування задачі
Критерії значущості забезпечують найкращу достовірність статистичних висновків‚ якщо вибірку беруть з нормально розподіленої генеральної сукупності. При відхиленнях від нормального розподілу точність критеріїв значущості дещо зменшується. На практиці використовують ряд розподілівё досить близьких до нормального: біноміальний, поліноміальний, розподіл Пуассона, розподіл Фішера, розподіл Стьюдента. Завданням куросового проекту є побудова теоретичного ряду з арозподілом Пуассона та перевірка гіпоетзи про узгодження теоретичного та емпіричного рядів за критерієм згоди ![]() (хі-квадрат) Пірсона.
(хі-квадрат) Пірсона.
Розподіл Пуассона є додатнім цілочисленим розподілом‚ який відіграє величезну роль в теорії ймовірностей та математичній статистиці. В якості прикладів випадкових величин‚ які розподілені за законом Пуассона‚ звичайно наводять наступні: число альфа-частинок‚ які випромінюються радіоактивним джерелом за певний проміжок часу; кількість бактерій‚ які видно під мікроскопом; число зірок в просторі і т.п. цей розподіл часто зустрічається при дослідженні проблем‚ пов'язаних з телефонною мережею.
Випадкова величина Х, яка має розподіл Пуассона, приймає значення ![]() , причому ймовірність
, причому ймовірність ![]() того, що вона прийме значення
того, що вона прийме значення ![]() , обчислюється за формулою
, обчислюється за формулою
![]() (5)
(5)
де ![]() , тобто параметр
, тобто параметр ![]() є математичним сподіванням випадкової величини Х. Знайдемо дисперсію випадкової величини Х:
є математичним сподіванням випадкової величини Х. Знайдемо дисперсію випадкової величини Х:
![]() ,
,
тобто параметр ![]() є середнім квадратичним відхиленням величини Х. Виконавши деякі перетворення‚ отримаємо
є середнім квадратичним відхиленням величини Х. Виконавши деякі перетворення‚ отримаємо ![]() .
.
Через параметр ![]() можна виразити ще дві характеристики розподілу Пуассона: коефіцієнт асиметрії
можна виразити ще дві характеристики розподілу Пуассона: коефіцієнт асиметрії ![]() і ексцес
і ексцес ![]() .
.
Однією з суттєвих особливостей розподілу Пуассона є його стійкість відносно лінійних операцій над випадковими величинами.
Тепер перейдемо до критерію Пірсона. Нехай теоретичний розподіл задано функцією (5)‚ а ![]() - теоретичні частоти відповідних значень
- теоретичні частоти відповідних значень ![]() ознаки
ознаки ![]() . Потрібно встановити‚ якою мірою розподіл Пуассона відображає емпіричний ряд. Щоб зробити висновок про міру узгодження між емпіричним і теоретичним розподілом‚ розглядають сумарну розбіжність між емпіричними
. Потрібно встановити‚ якою мірою розподіл Пуассона відображає емпіричний ряд. Щоб зробити висновок про міру узгодження між емпіричним і теоретичним розподілом‚ розглядають сумарну розбіжність між емпіричними ![]() та теоретичними
та теоретичними ![]() частотами. Сумарна розбіжність між частотами залежить від функції розподілу‚ який дає нам теоретичні частоти‚ і від випадкових причин‚ внаслідок яких маємо емпіричний розподіл. Якщо сумарна розбіжність мала‚ то можна припустити‚ що вона зумовлена випадковими причинами‚ а тому теоретичний розподіл добре відображає емпіричний ряд. Якщо сумарна розбіжність велика‚ то вона зумовлена істотними причинами‚ а саме тим‚ що теоретичний розподіл погано відображає емпіричний ряд.
частотами. Сумарна розбіжність між частотами залежить від функції розподілу‚ який дає нам теоретичні частоти‚ і від випадкових причин‚ внаслідок яких маємо емпіричний розподіл. Якщо сумарна розбіжність мала‚ то можна припустити‚ що вона зумовлена випадковими причинами‚ а тому теоретичний розподіл добре відображає емпіричний ряд. Якщо сумарна розбіжність велика‚ то вона зумовлена істотними причинами‚ а саме тим‚ що теоретичний розподіл погано відображає емпіричний ряд.
Критерій згоди Пірсона полягає в тому‚ що за міру розбіжності між емпіричними і теоретичними частотами беруть величину
![]() . (6)
. (6)
Величина ![]() - середня зважена квадратів відхилень емпіричних і теоретичних частот‚ при цьому вагою є величини‚ обернені теоретичним частотам. Статистика
- середня зважена квадратів відхилень емпіричних і теоретичних частот‚ при цьому вагою є величини‚ обернені теоретичним частотам. Статистика ![]() є випадковою величиною‚ яка сама має свій закон розподілу. Пірсон показав‚ що
є випадковою величиною‚ яка сама має свій закон розподілу. Пірсон показав‚ що ![]() не залежить ні від функції розподілу‚ ні від обсягу вибірки‚ а залежить лише від параметра
не залежить ні від функції розподілу‚ ні від обсягу вибірки‚ а залежить лише від параметра ![]() - числа степенів свободи і дорівнює різниці між числом частот
- числа степенів свободи і дорівнює різниці між числом частот ![]() ‚ які порівнюються і числом зв'язків‚ які на ці частоти накладено. При застосуванні критерію Пірсона вважають‚ що сума теоретичних частот дорівнює сумі емпіричних‚ а теоретичні середня і дисперсія дорівнюють вибірковій середній і вибірковій дисперсії. Тому число степенів вільності (свободи) становить
‚ які порівнюються і числом зв'язків‚ які на ці частоти накладено. При застосуванні критерію Пірсона вважають‚ що сума теоретичних частот дорівнює сумі емпіричних‚ а теоретичні середня і дисперсія дорівнюють вибірковій середній і вибірковій дисперсії. Тому число степенів вільності (свободи) становить ![]() .
.
Критерій Пірсона застосовують за таким алгоритмом.
1. Формулюють гіпотезу H0 - емпіричний розподіл відповідає розподілу Пуассона і альтернативну гіпотезу - емпіричний розподіл не відповідає розподілу Пуассона.
2. Задають рівень значущості ![]() .
.
3. Розглядають вибірку обсягом ![]() незалежних спостережень і емпіричний розподіл представляють у вигляді інтервального варіаційного ряду.
незалежних спостережень і емпіричний розподіл представляють у вигляді інтервального варіаційного ряду.
4. Обчислюють вибіркові характеристики ![]() і S. Їх використовують замість генерального параметра розподілу Пуассона‚ з яким порівнюватимемо емпіричний розподіл.
і S. Їх використовують замість генерального параметра розподілу Пуассона‚ з яким порівнюватимемо емпіричний розподіл.
5. Обчислюють значення теоретичних частот ![]() для кожнго з інтервалів групування. Для цього використовується формула
для кожнго з інтервалів групування. Для цього використовується формула
![]()
Якщо буде встановлено‚ що обчислені частоти ![]() деяких інтервалів групування менше п'яти‚ то сусідні інтервали об'єднуються так‚ щоб сума обчислених теоретичних частот була не меншою п'яти. Частоти об'єднаних інтервалів при цьому додають.
деяких інтервалів групування менше п'яти‚ то сусідні інтервали об'єднуються так‚ щоб сума обчислених теоретичних частот була не меншою п'яти. Частоти об'єднаних інтервалів при цьому додають.
6. Обчислюють значення критерію ![]() за формулою (6).
за формулою (6).
7. Знаходять табличне критичне значення ![]() для заданого рівня значущості
для заданого рівня значущості ![]() і числа ступенів свободи
і числа ступенів свободи ![]() .
.
8. Якщо ![]() ‚ то емпіричний розподіл не відповідає розподілу Пуассона при заданому рівні значущості
‚ то емпіричний розподіл не відповідає розподілу Пуассона при заданому рівні значущості ![]() . Якщо
. Якщо ![]() ‚ то це дає право стверджувати‚ що гіпотеза H0 допустима‚ тобто припущення про те‚ що в генеральній розподіл не суперечить дослідним даним.
‚ то це дає право стверджувати‚ що гіпотеза H0 допустима‚ тобто припущення про те‚ що в генеральній розподіл не суперечить дослідним даним.
В розділі 2 описано програму визначення ступеня згоди емпіричного розподілу з теоретичним розподілом Пуассона.
Похожие работы
... ів. Негативно класифіковані активи – це «сумнівна» та «безнадійна» заборгованість за основною сумою боргу, прострочені понад 31 день та сумнівні відсотки. 2.2 Міжнародні підходи щодо класифікації кредитного портфеля банку В процесі багатовікового та динамічного розвитку банківської системи створювались все нові підходи до класифікації кредитного портфеля, що дає змогу банкам оцінити якість ...
... ів загальновиробничих та загальногосподарських витрат, капітального ремонту, списання матеріалів на обсяг виробництва продукції або будівельних матеріалів, на обсяг виконаних будівельно-монтажних робіт 13. Нормативні перевірки Застосовуються аудитором для отримання доказів про виконання певного завдання. На підставі цих даних аудитор оцінює дотримання показників і розробляє пропозиції, які ...
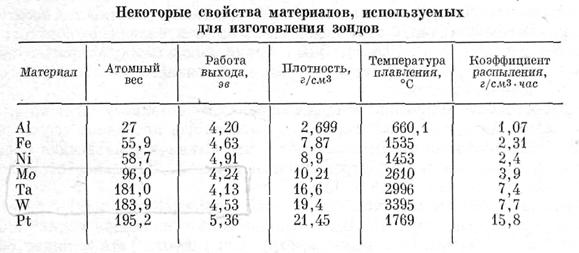
... до спеціальних керамічних матеріалів, таких, як спеченний окис алюмінію і різні сполуки магнію, кремнію і цирконію у випадку гарячих плазм. 2. Потенціал електростатичного зонду в плазмовому гетерогенному середовищі. Зазвичай лінійні розміри зондів, що використовуються для діагностики запиленої плазми лежать в інтервалі [0.1, 10.0] мм та помітно перевищують як дебаєвську довжину електронного ...
... программного обеспечения: критерии, оценки, метод выбора // НТУУ КПІ, 2005, VII МНПК “Системний аналіз та інформаційні технології”, Київ, 2005. С.189. АНОТАЦІЯ Дідковська М. В. Методи оцінки та засоби підвищення надійності програмного забезпечення. – Рукопис. Дисертація на здобуття наукового ступеня кандидата технічних наук за спеціальністю 05.13.06 – “Автоматизовані системи управління та ...
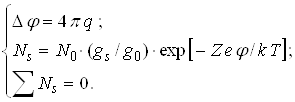
0 комментариев