Синтез автоматів з пам’яттю

Полтавський Військовий Інститут Зв’язку

Кафедра схемотехніки радіоелектронних систем

 

ОБЧИСЛЮВАЛЬНА ТЕХНІКА ТА МІКРОПРОЦЕСОРИ

напрям підготовки 0924 «Телекомунікації»

 

Синтез автоматів з пам’яттю.

Полтава – 2006

Навчальна література.

 

1.         Тиртишніков О.І. Обчислювальна техніка та мікропроцесори. Частина 2. Цифрові автомати: Навчальний посібник. – Полтава: ПВІЗ, 2006. с. 62-71.

2.         Калабеков Б.А., Мамзелев И.А. Цифровые устройства и микропроцессорные системы. М.: Радио и связь, 1987.

1.         Алгоритм синтезу послідовнісних ЦА.

 

Головною метою синтезу ЦА з пам’яттю є визначення всіх його можливих станів та переходів, відповідно заданому алгоритму функціонування, та отримання функцій збудження всіх входів тригерів, з яких складається автомат. Цього достатньо для складання логічної схеми ЦА з урахуванням заданого схемотехнічного базису.

Багатоваріантність можливих реалізацій ЦА пов’язана з вибором типу тригерів та способу побудови його комбінаційної частини. Теоретично будь-який ЦА може бути побудований на тригерах будь-якого типу. Найбільш розповсюджені в схемотехніці D- та JK-тригери. JK-тригер має більш розвинені логічні можливості, тому для нього можна отримати більш прості функції збудження, але кількість функцій буде удвічі більшою, ніж для D-тригера. Яке рішення буде оптимальним для конкретного ЦА, заздалегідь невідомо.

Алгоритм синтезу ЦА з пам’яттю містить такі основні етапи:

1.         Запис та формалізація умов функціонування автомата. Як і для комбінаційних пристроїв, вихідне завдання функціонування ЦА з пам’яттю може виконуватися в різних формах, у тому числі і словесній. У результаті формалізації необхідно отримати таблиці або формули, що повно та однозначно описують алгоритм функціонування ЦА у всіх можливих режимах роботи.

2.         Мінімізація та кодування станів. На цьому етапі необхідно визначити мінімальну кількість всіх можливих станів ЦА з урахуванням всіх необхідних напрямків переходу. Кодування станів найчастіше виконується з використанням двійкових кодів. Якщо ЦА може функціонувати в декількох різних режимах, доцільно скласти граф переходів (діаграму станів), що наочно відображає як можливі стани ЦА, так і напрямки переходів у різних режимах функціонування.

3.         Складання таблиці переходів. На основі діаграми станів (для ЦА, режим роботи яких завжди однаковий – безпосередньо на основі вихідної таблиці) складається таблиця переходів, в якій необхідно показати не тільки попередні та наступні стани тригерів, але і сигнали на їх входах.

4.         Визначення функцій збудження тригерів. Функції збудження тригерів отримують із таблиці переходів, звичайно у вигляді ДДНФ, таким же чином, що і для комбінаційних схем. Попередні стани тригерів при цьому використовуються як вхідні аргументи функцій.

5.         Мінімізація функцій збудження тригерів. Функції збудження тригерів реалізовуються комбінаційною частиною автомата, що в загальному випадку має n + m входів (n – кількість вхідних сигналів ЦА, m – кількість виходів всіх тригерів ЦА) та l + k виходів (l – кількість вихідних сигналів ЦА, k – кількість входів всіх тригерів ЦА). Це пояснюється узагальненою структурною схемою послідовнісного ЦА, що зображена на рис.1. Тобто, на цьому етапі виконується спільна мінімізація l + k логічних функцій n + m аргументів. Для мінімізації функцій використовуються будь-які існуючі методи – наприклад, карти Карно.

Рис. 1. Узагальнена структурна схема послідовнісного ЦА

6.         Перехід до заданого базису та складання логічної схеми ЦА виконуються практично таким же чином, що і при синтезі комбінаційних схем. Однак, слід мати на увазі, що поняття логічного базису застосовується лише до комбінаційної частини ЦА, але не відноситься до пам’яті автомата (тип тригерів, що реалізовують пам'ять ЦА, визначається вихідними умовами задачі або вибирається проектувальником).

Завершується проектування ЦА його аналізом – тобто моделюванням або макетуванням отриманої схеми з метою перевірки правильності її функціонування.

2.         Приклад синтезу послідовнісного ЦА.

 

Поставлення завдання (вихідне завдання функціонування): необхідно синтезувати трирозрядний додаючий двійковий лічильник на основі Т-тригерів, алгоритм функціонування якого визначає керуючий сигнал М. Якщо М = 0, лічильник працює як звичайний лічильник прямого рахування; якщо М = 1, лічильник працює в коді Грея. Зміна керуючого сигналу М відразу веде до зміни режиму роботи, тобто наступний стан лічильника буде належати вже іншому коду.

Синтез проведемо без обмежень на використовуваний логічний базис з метою отримання схеми з мінімальною кількістю елементів.

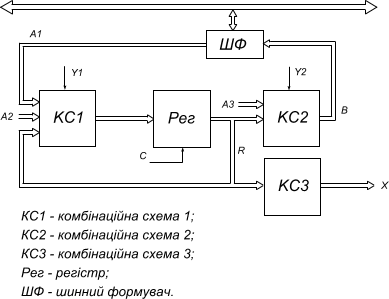
На основі опису ЦА можливо відразу отримати його структурну схему, що зображена на рис. 2.

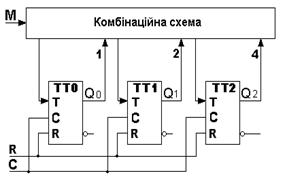
Рис. 2. Структурна схема ЦА

 

Комбінаційна схема реалізує необхідні функції збудження Т-тригерів на основі їх станів та керуючого сигналу М. Всі тригери мають загальні входи скидання та синхронізації.

1.   Формалізоване завдання функціонування. Мінімізація та кодування станів автомата. Алгоритм функціонування лічильника в обох заданих режимах може бути поданий табл. 1.

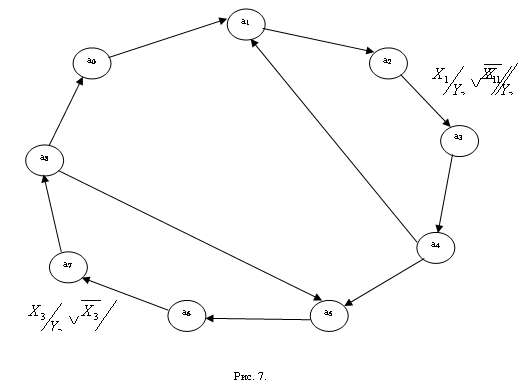
На підставі табл. 1 складемо граф переходів (діаграму станів) лічильника, що показана на рис. 3. Напрямки переходів на діаграмі вказані: для рахування в коді 8421 – пунктирними лініями, для рахування в коді Грея – суцільними лініями. Ділянки діаграми, де напрямки переходів у двох режимах співпадають, вказані подвійними лініями.

Таблиця 1

Такт	М=0; код 8421			М=1; код Грея
	Х2	Х1	Х0	Х2	Х1	Х0
Початковий стан	0	0	0	0	0	0
1	0	0	1	0	0	1
2	0	1	0	0	1	1
3	0	1	1	0	1	0
4	1	0	0	1	1	0
5	1	0	1	1	1	1
6	1	1	0	1	0	1
7	1	1	1	1	0	0

 

Рис.3. Діаграма станів лічильника

 

2.         Складання таблиці переходів автомата. На підставі діаграми станів з урахуванням алгоритму функціонування Т-тригера складаємо таблицю переходів ЦА (табл. 2).

Таблиця 2

М	Початковий стан			Наступний стан			Сигнали на входах тригерів
							Т2	Т1	Т0
0	0	0	0	0	0	1	0	0	1
0	0	0	1	0	1	0	0	1	1
0	0	1	0	0	1	1	0	0	1
0	0	1	1	1	0	0	1	1	1
0	1	0	0	1	0	1	0	0	1
0	1	0	1	1	1	0	0	1	1
0	1	1	0	1	1	1	0	0	1
0	1	1	1	0	0	0	1	1	1
1	0	0	0	0	0	1	0	0	1
1	0	0	1	0	1	1	0	1	0
1	0	1	0	1	1	0	1	0	0
1	0	1	1	0	1	0	0	0	1
1	1	0	0	0	0	0	1	0	0
1	1	0	1	1	0	0	0	0	1
1	1	1	0	1	1	1	0	0	1
1	1	1	1	1	0	1	0	1	0