Навигация
Опис мінімізації БФ заданими методами
1.3 Опис мінімізації БФ заданими методами
Для вибору мінімальної з МДНФ і МКНФ оцінимо складність схеми за допомогою ціни по Квайну. Ціна по Квайну визначається як сумарне число входів логічних елементів у складі схеми.
Такий підхід обумовлений тим, що
- складність схеми легко обчислюється по БФ, на основі яких будується схема: для ДНФ складність дорівнює сумі кількості літер, (літері зі знаком відповідає ціна 2), і кількість знаків диз’юнкції, збільшеного на 1 для кожного диз’юнктивного виразу.
- усі класичні методи мінімізації БФ забезпечують мінімальність схемі саме у змісті ціни по Квайну.
Схема с мінімальною ціною по Квайну часто реалізується з найменшим числом конструктивних елементів – корпусів інтегральних мікросхем.
Для даних функцій ми маємо:
Cкв (МДНФ)=19+6+5=30;
Cкв(МКНФ)=21+6+5=32.
Так як мінімальною ціною є Cкв(МКНФ), то для реалізації схеми будемо використовувати МДНФ.
1.4 Приведення БФ до заданого базису
Заданий базис: 3 І-НІ.
Приведемо вираз до заданого базису:
_ _ _ _ _ _ _ _ _ _ _ _ _
![]() Y=X1X3X4+X2X4X5+X3X4X5+X1X2X3X4+X1X4X5+X1X3X4 =
Y=X1X3X4+X2X4X5+X3X4X5+X1X2X3X4+X1X4X5+X1X3X4 =
=X3(X1X4*X4X5*X1X2X4)*X5(X2X4*X1X4)*X1X3X4
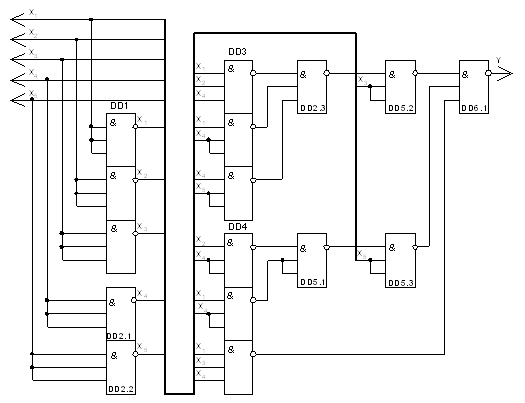
Для реалізації функції по останьому виразу необхідно 16 елементів 3І-НІ (Рис.1). Ранг даної схеми дорівнює 4, що негативно відображається на швидкості. Використав факторний алгоритм можливо покращити схему, збільшити швидкість його роботи.
Рис. 1 Функціональна схема для заданого базису
2. Проектування автоматів
2.1 Вибір завдання
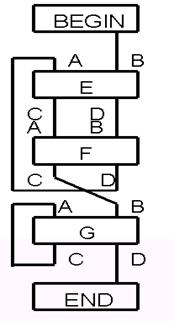
Граф-схеми алгоритмів обираються кожним студентом в індивідуальному порядку. Вона складається з чотирьох блоків: E, F, G, H. Студенти обирають граф-схему із п’яти блоків з номерами 0...4 на підставі чисел А, В, С та (А+В+С) за наступними правилами:
- блок "Е" – схема під номером (А) mod 5 = 13 mod 5 = 3;
- блок "F" – схема під номером (В) mod 5 = 7 mod 5 = 2;
- блок "G" – схема під номером (С) mod 5 = 21 mod 5 = 1;
- блок "H" – схема під номером (А+В+С) mod 5 = 41 mod 5 = 1.
Розташування обирається з використанням номера групи. Тип тригера знаходимо по таблиці на підставі числа (А) mod 3 = 13 mod 3 = 1.
| (A) mod 3 | ТИП ТРИГЕРА | |
| 0 | Т | D |
| 1 | D | JK |
| 2 | JK | T |
| автомат | Мілі | Мура |
Отримуємо D-тригер для автомата Мілі та JK-тригер для Мура. Для парних номерів за списком (21) - серія КР555.
Після відповідної розмітки будуємо таблиці переходів для обох автоматів.
2.2 Автомат Мура:
Будуємо таблицю переходів для автомата Мура.
Кодування станів виконуємо за еврістичним алгоритмом. Для цього будуємо матрицю Т.
║T║ =
i │ j │ P(i,j)
1 │ 2 │ 1
1 │ 24│ 1
1 │ 25│ 1
2 │ 4 │ 1
2 │ 6 │ 1
2 │ 7 │ 1
3 │ 5 │ 1
3 │ 6 │ 1
3 │ 7 │ 1
3 │ 13 │ 1
3 │ 14 │ 1
4 │ 6 │ 1
4 │ 7 │ 1
5 │ 6 │ 1
5 │ 7 │ 2
6 │ 8 │ 1
6 │ 9 │ 1
7 │ 8 │ 1
8 │ 10 │ 1
9 │ 11 │ 1
10│ 11 │ 1
10│ 13 │ 1
10│ 14 │ 1
11│ 12 │ 1
11│ 13 │ 1
12│ 15 │ 1
13│ 15 │ 1
15│ 17 │ 1
15│ 19 │ 1
15│ 20 │ 1
16│ 19 │ 1
16│ 20 │ 2
16│ 22 │ 2
16│ 26 │ 1
17│ 18 │ 1
18│ 21 │ 1
19│ 21 │ 1
20│ 22 │ 1
21│ 23 │ 1
21│ 25 │ 1
21│ 26 │ 1
22│ 25 │ 1
22│ 26 │ 2
23│ 24 │ 1
Підкрашуємо вагу всіх компонентів всіх пар
P(1) = 3
P(2) = 4
P(3) = 5
P(4) = 3
P(5) = 3
P(6) = 6
P(7) = 5
P(8) = 3
P(9) = 2
P(10) = 4
P(11) = 4
P(12) = 2
P(13) = 4
P(14) = 2
P(15) = 5
P(16) = 4
P(17) = 2
P(18) = 2
P(19) = 3
P(20) = 3
P(21) = 5
P(22) = 4
P(23) = 2
P(24) = 2
P(25) = 3
P(26) = 3
Далі згідно правил алгоритму будуємо матрицю М
║M║ =
i │ j │ P(i,j)
5 │ 7 │ 2
3 │ 7 │ 1
3 │ 6 │ 1
2 │ 6 │ 1
2 │ 7 │ 1
3 │ 13 │ 1
4 │ 6 │ 1
5 │ 6 │ 1
6 │ 8 │ 1
13 │ 15 │ 1
3 │ 5 │ 1
4 │ 7 │ 1
6 │ 9 │ 1
7 │ 8 │ 1
10 │ 13 │ 1
10 │ 11 │ 1
11 │ 13 │ 1
15 │ 19 │ 1
15 │ 20 │ 1
16 │ 20 │ 2
16 │ 22 │ 2
22 │ 26 │ 2
19 │ 21 │ 1
21 │ 25 │ 1
21 │ 26 │ 1
1 │ 2 │ 1
2 │ 4 │ 1
3 │ 14 │ 1
8 │ 10 │ 1
12 │ 15 │ 1
15 │ 17 │ 1
16 │ 19 │ 1
16 │ 26 │ 1
18 │ 21 │ 1
20 │ 22 │ 1
21 │ 23 │ 1
22 │ 25 │ 1
1 │ 25 │ 1
9 │ 11 │ 1
10 │ 14 │ 1
11 │ 12 │ 1
1 │ 24 │ 1
17 │ 18 │ 1
23 │ 24 │ 1
Визначемо розрядність кода для кодування станів автомата
R = ] log2 N [ = ] log2 26 [ = 5
Результати кодування:
a1 10101
a2 00101
a3 00010
a4 00111
a5 00000
a6 00011
a7 00001
a8 01011
a9 10011
a10 01010
a11 11010
a12 11110
a13 10010
a14 01000
a15 10110
a16 00100
a17 10111
a18 11111
a19 10100
a20 00110
a21 11101
a22 01100
a23 11001
a24 10001
a25 11100
a26 01101
Підрахунок ефективності кодування:
Кількість перемикань тригерів:
W = E P(i,j)*d(i,j) = P(1,2)*d(1,2) + P(1,24)*d(1,24) + P(1,25)*d(1,25) + P(2,4)*d(2,4) + P(2,6)*d(2,6) + P(2,7)*d(2,7) + P(3,5)*d(3,5) + P(3,6)*d(3,6) + P(3,7)*d(3,7) + P(3,13)*d(3,13) + P(3,14)*d(3,14) + P(4,6)*d(4,6) + P(4,7)*d(4,7) + P(5,6)*d(5,6) + P(5,7)*d(5,7) + P(6,8)*d(6,8) + P(6,9)*d(6,9) + P(7,8)*d(7,8) + P(8,10)*d(8,10) + P(9,11)*d(9,11) + P(10,11)*d(10,11) + P(10,13)*d(10,13) + P(10,14)*d(10,14) + P(11,12)*d(11,12) + P(11,13)*d(11,13) + P(12,15)*d(12,15) + P(13,15)*d(13,15) + P(15,17)*d(15,17) + P(15,19)*d(15,19) + P(15,20)*d(15,20) + P(16,19)*d(16,19) + P(16,20)*d(16,20) + P(16,22)*d(16,22) + P(16,26)*d(16,26) + P(17,18)*d(17,18) + P(18,21)*d(18,21) + P(19,21)*d(19,21) + P(20,22)*d(20,22) + P(21,23)*d(21,23) + P(21,25)*d(21,25) + P(21,26)*d(21,26) + P(22,25)*d(22,25) + P(22,26)*d(22,26) + P(23,24)*d(23,24) = 1*1 + 1*1 + 1*2 + 1*1 + 1*2 + 1*1 + 1*1 + 1*1 + 1*2 + 1*1 + 1*2 + 1*1 + 1*2 + 1*2 + 2*1 + 1*1 + 1*1 + 1*2 + 1*1 + 1*2 + 1*1 + 1*2 + 1*1 + 1*1 + 1*1 + 1*1 + 1*1 + 1*1 + 1*1 + 1*1 + 1*1 + 2*1 + 2*1 + 1*2 + 1*1 + 1*1 + 1*2 + 1*2 + 1*1 + 1*1 + 1*1 + 1*1 + 2*1 + 1*1 = 60
Мінімально можлива кількість перемикань тригерів:
Wmin = E P(i,j) = 48
Коефіціент ефективності кодування: 1.25
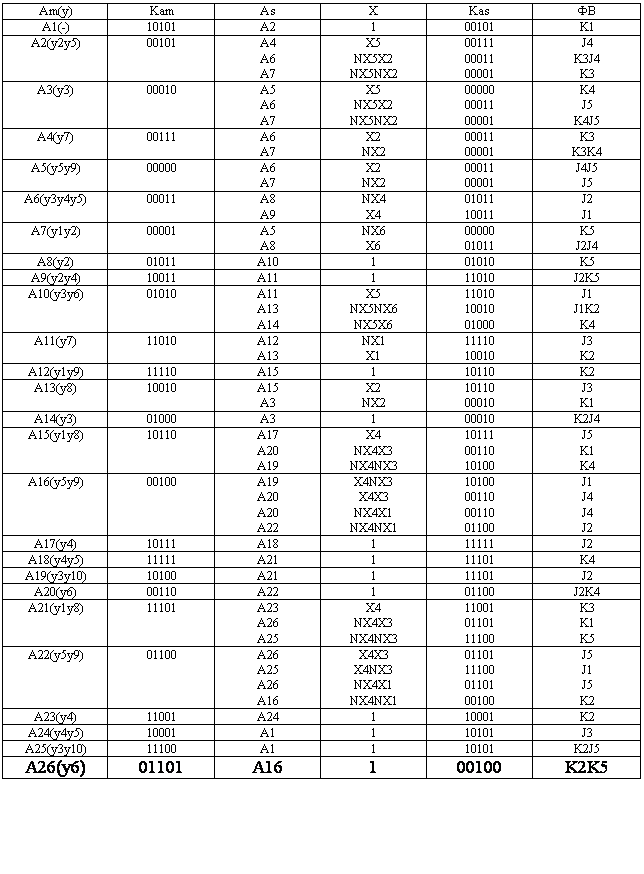 Виписуємо з таблиці вирази для тригерів (та виконуємо необхідні перетворення для представлення їх в рамках потрібної серії):
Виписуємо з таблиці вирази для тригерів (та виконуємо необхідні перетворення для представлення їх в рамках потрібної серії):
J1=a6*x4+a8+a11*x1+a11*nx1+a21*x4+a22*nx4*nx1=
a6*x4+a8+a11+a21*x4+a22*nx4*nx1
K1=a3*x5+a3*nx5*x2+a3*nx5*nx2+a9+a10*x5+a15*nx4*x3+a16*x4*x3+a16*nx4*x1+a16*nx4*nx1+a17+a19+a24+a26=
a3*x5+a3+a9+a10*x5+a15*nx4*x3+a16*x4*x3+a16+a17+a19+a24+a26
J2=a2*x5+a9+a10*x5+a10*nx5*x6+a15*nx4*nx3+a16*x4*nx3+a16*nx4*nx1+
a18+a20+a21*nx4*nx3+a24
K2=a1+a4*x2+a4*nx2+a11*x1+a12+a14+a19+a22*x4*x3+a22*nx4*x1+
a22*nx4*nx1=
a1+a4+a11*x1+a12+a14+a19+a22*x4*x3+a22
J3=a1+a6*nx4+a7*x6+a15*x4+a19+a22*x4*x3+a22*x4*nx3+a22*nx4*x1+
a22*nx4*nx1=
a1+a6*nx4+a7*x6+a15*x4+a19+a22
K3=a2*x5+a2*nx5*x2+a2*nx5*nx2+a10*x5+a10*nx5*nx6+a10*nx5*x6+
a16*x4*nx3+a16*x4*x3+a16*nx4*x1+a16*nx4*nx1+a24+a25=
a2+a10+a16+a24+a25
J4=a1+a3*x5+a6*x4+a7*nx6+a10*nx5*x6+a13*x2+a16*x4*x3+a16*nx4*x1+
a16*nx4*nx1+a17+a19=
a1+a3*x5+a6*x4+a7*nx6+a10*nx5*x6+a13*x2+a16*x4*x3+a16*nx4+a17+a19
K4=a2*nx5*x2+a2*nx5*nx2+a4*x2+a4*nx2+a5*x2+a5*nx2+a9+a14+a15*x4+
a15*nx4*nx3+a21*nx4*x3+a21*nx4*nx3+a22*x4*x3+a22*x4*nx3+a22*nx4*x1+a22*nx4*nx1+a24=
a2*nx5+a4+a5+a9+a14+a15*x4+a15*nx4*nx3+a21*nx4+a22+a24
J5=a1+a3*x5+a3*nx5*nx2+a6*nx4+a6*x4+a23=a1+a3*x5+a3*nx5*nx2+a6+a23
K5=a4*x2+a5*x2+a10*nx5*x6+a12+a13*x2+a13*nx2+a24=
a4*x2+a5*x2+a10*nx5*x6+a12+a13+a24
Для підвищення функціональності схеми можна виділити однакові елементи:
Z1 = nx5+nx6 Z5 = nx4+x1
Z2 = x4+nx3 Z6 = nx4+x3Z3 = nx4+nx1 Z7 = nx4+nx3
Z4 = x4+x3
Виконуємо необхідні перетворення для представлення ФЗ в рамках потрібної серії:
J1=a6*x4+a10*x5+a10*z1+a16*z2+a22*z2=n((na6+nx4)(na10+nx5)(na10+nz1)(na16+nz2)(na22+nz2))
J2=a6*nx4+a7*x6+a9+a16*z3+a17+a19+a20=n((na6+x4)(na7+nx6)(na16+nz3)*na9*na17*na19*na20)
J3=a3*nx1+a13*x2+a24=n((na3+x1)(na13+nx2)*na24)
J4=a2*x5+a2*nx5*x2+a5*x2+a7*x6+a14+a16*z4+a16*z5=n((na2+nx5)*
(na2+n(nx5*x2))(na5+nx2)(na7+nx6)(na16+nz4)(na16+nz5)*na14)
J5=a3*nx5+a5+a15*x4+a22*z4+a22*z5+a25=n((na3+x5)(na15+nx4)*
(na22+nz4)(na22+nz5)*na5*na25)
K1=a1+a13*nx2+a15*z6+a21*z6=n((na1*(na13+x2)(na15+nz6)(na21+nz6))
K2=a10*z1+a11*x1+a12+a14+a22*z3+a23+a25+a26=n((na10+nz1)(na11+nx1)(na22+nz3)*na12*na14*na23*na25*na26) K3=a2*nx5+a4+a21*x4=n((na2+x5)(na21+nx4)*na4)K4=a3*x5+a3*nx5*nx2+a4*nx2+a10*nx5*x6+a15*z7+a18+a20=n((na3+ nx5)(na3+n(nx5*nx2))(na4+x2)((na10+n(nx5*x6))(na15+nz7)*na18*na20)
K5=a7*nx6+a8+a9+a21*z7+a26=n((na7+x6)(na21+nz7)*na8*na9*na26)
Формуємо функції виходів автомата:Y1=a7+a12+a15+a21=n(na7*na12*na15*na21)
Y2=a2+a7+a8+a9=n(na2*na7*na8*na9)
Y3=a3+a6+a10+a14+a19+a25=n(na3*na6*na10*na14*na19*na25)
Y4=a6+a9+a17+a18+a23+a24=n(na6*na9*na17*na18*na23*na24)
Y5=a2+a5+a6+a16+a18+a22+a24=n(na2*na5*na6*na16*na18*na22*na24)
Y6=a10+a20+a26=n(na10*na20*na26)
Y7=a4+a11=n(na4*na11)
Y8=a13+a15+a21=n(na13*na15*na21)
Y9=a5+a12+a16+a22=n(na5*na12*na16*na22)
Y10=a19+a25=n(na19*na25)
Ми отримали усі необхідні вирази для принципової схеми. Будуємо її, користуючись формулами для тригерів та вихідними станами (Лист 1).
Похожие работы
... функції менше, ніж МКНФ, обираємо для реалізації МДНФ функції. Реалізацію будемо проводити згідно з заданим базисом 2ЧИ-НІ. Застосуємо до обраної форми факторний алгоритм та одержимо скобкову форму для заданої функції: у = у = у = 2. Вибір блоків та структури ГСА Граф-схеми алгоритмів обираються кожним студентом індивідуально. Граф-схема складається з трьох блоків E, F, G і вершин ...
... Таблиця переходів автомата 2.2.3. Кодування станів 2.2.5. Функції збудження тригерів та вихідних сигналів Закінчення Список використаної літератури 1 Введення Метою курсового проекту по дисципліні "Прикладна теорія цифрових автоматів" є закріплення основних теоретичних знань і практичних навичок у ході самостійної роботи. У ході роботи необхідно :1. спроектувати керуючий автомат Милі по ...
... льш прості операції які називаються мікроопераціями тобто кожна операція – це визначена послідовність мікрооперацій. Існують два основні типи керуючих автоматів 1. Керуючий автомат з жорсткою чи схемною логікою. Для кожної операції будується набір комбінаційних схем які в потрібних тактах збуджують відповідні керуючі сигнали. Іншими словами ...
... автомата повинна містити певну кількість логічний елементів, що утворюють функціонально повну систему для синтезу необхідної комбінаційної схеми. 1.5 Контроль виконання арифметичних операцій Арифметичні операції виконуються на суматорах прямого, оберненого і доповняльного коду. Припустимо, що зображення чисел зберігаються в машині в деякому коді, тобто операція перетворення в заданий код або ...
0 комментариев