Навигация
Задание цвета и размера маркеров
1. Задание цвета и размера маркеров
Помимо цвета и стиля, имеется также возможность задавать и другие графические харак-теристики линий (более подробное описание этих свойств дано в описании функции line):
• LineWidth – задание ширины линии в точках (points), где 1 точка равна 1/72 дюйма.
• MarkerEdgeColor – задание цвета маркера или цвета граней маркера для «заполненных» маркеров (кружков, квадратов, ромбов, пентаграмм (пятиугольников), гексаграмм (шести-угольников), и четырех типов треугольников).
• MarkerFaceColor – задание цвета поверхности заполненных маркеров.
• MarkerSize – задание размера маркера в единицах точки.
Например, выражения
x = -pi : pi/10 : pi;
y = tan(sin(x)) - sin(tan(x));
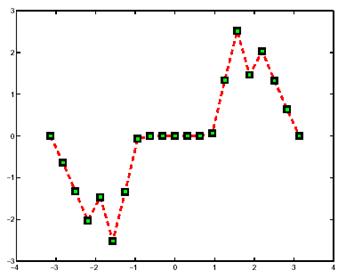
plot(x, y, '--rs', 'LineWidth', 2,...
'MarkerEdgeColor', 'k',...
'MarkerFaceColor', 'g',...
'MarkerSize', 10)
дают следующий график
2. Задание положений меток (Tick-Mark) и указание надписей (Labeling)
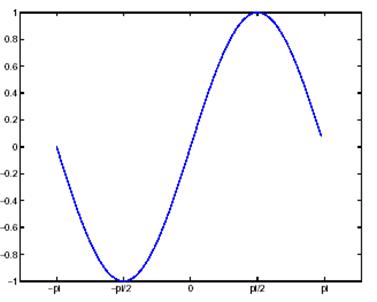
Вы имеете возможность устанавливать положение меток на осях, а также вид надписей на каждой метке. Например, в следующем графике синусоидальной функции производится изменение маркировки оси x, с целью придания более значимых и информативных значений меток и их надписей:
x = -pi : 0.1 : pi;
y = sin(x);
plot(x, y)
set(gca, 'XTick',-pi : pi/2 : pi)
set(gca, 'XTickLabel',{'-pi', '-pi/2', '0', 'pi/2', 'pi'})
Добавление заголовков, надписей к осям и аннотаций
Добавим теперь надписи к осям и комментарий к точке -pi/4, sin(-pi/4).
Следующие три стандартные команды позволяют ввести надписи к осям x и y, а также общий заголовок к графику
xlabel('-\pi \leq \Theta \leq \pi')
ylabel('sin(\Theta)')
title('Plot of sin(\Theta)')
а команда text дает возможность ввести текстовую информацию в любую выбранную точ-ку координатных осей
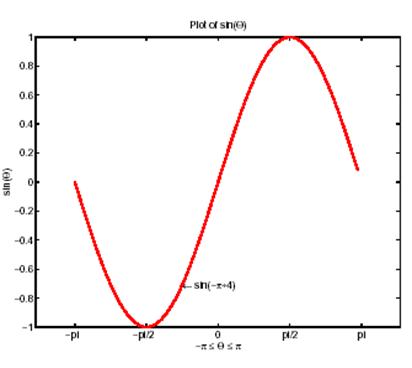
text(-pi/4, sin(-pi/4), '\leftarrow sin(-\pi\div4)', 'HorizontalAlignment', 'left')
Изменим также цвет линии на красный, находя сперва дескриптор линии, созданной фун-кцией plot, а затем установив требуемое свойство линии Color property. В том же выраже-нии установим толщину линии LineWidth равной двум точкам
set(findobj(gca, 'Type', 'line', 'Color', [0 0 1]),...
'Color','red',,...
'LineWidth', 2)
См. также функции:
axis, bar, grid, legend, line, LineSpec, loglog, plotyy, semilogx, semilogy, subplot, xlabel,
xlim, ylabel, ylim, zlabel, zlim, stem
См. свойство String функции text , где дается список символов и описывается их приме-нение.
LineSpec
Назначение. Спецификации задания свойств графического объекта линия (Line).
Описание. В данном разделе описывается как можно задать свойства линий, используе-мых при построении графиков. Система MATLAB дает возможность задавать многие ха-рактеристики, включая:
Стиль линии (Line style) Толщину линии (Line width) Цвет (Color) Тип маркера (Marker type) Размер маркера (Marker size) Цвета поверхности и граней маркера (для заполненных маркеров)
MATLAB предусматривает специальные символьные спецификаторы (описатели) для сти-лей линий, типов маркеров и цветов. В следующих таблицах дается перечисление этих спецификаторов.
Спецификаторы стилей линии| Спецификаторы | Стили линии |
| - | Сплошная линия (по умолчанию) |
| -- | Штриховая линия |
| : | Пунктирная линия |
| -. | Штрих-пунктирная линия |
| Спецификаторы | Типы маркеров |
| + | Знак плюс |
| o | Кружочек |
| * | Звездочка |
| . | Точка |
| x | Крестик |
| s | Квадрат |
| d | Ромб |
| ^ | Треугольная стрелка вверх |
| v | Треугольная стрелка вниз |
| > | Треугольная стрелка направо |
| < | Треугольная стрелка налево |
| p | Пятиугольная звезда (пентаграмма) |
| h | Шестиугольная звезда (гексаграмма) |
Спецификаторы цвета
| Спецификатор | Цвет |
| r | Красный |
| g | Зеленый |
| b | Синий |
| c | Голубой (cyan) |
| m | Магента (magenta) |
| y | Желтый |
| k | Черный |
| w | Белый |
Многие графические функции допускают аргумент LineSpec, который определяет три спецификатора для характеристики линии:
Стиль линии Тип маркера ЦветНапример, функция plot(x, y, '-.or') строит график значений y от аргумента x, используя штрих-пунктирную линию (-.); размещает круглые маркеры (o) в точках данных, и окра-шивает как линию, так и маркеры в красный цвет (r). Данные спецификаторы нужно задать (в любом порядке) как строка символов в кавычках, после записей массивов данных. Если вы задаете в LineSpec только маркеры, но не стиль линии (например, plot(x,y,'d')), MATLAB наносит только маркеры (без линий)
Связанные (родственные) свойства. При использовании функций plot и plot3, вы можете задавать также другие характеристики линий, используя следующие графические свойства:
LineWidth – задает ширину линии (в точках, равных 1/72 дюйма) MarkerEdgeColor – задает цвет маркера или цвет граней для заполненных маркеров (кружок, квадрат, ромб, пентаграмма, гексаграмма, и четыре треугольника). MarkerFaceColor – задает цвет поверхности заполненного маркера MarkerSize – задает размер маркера в точкахВ дополнение, вы можете задавать графические свойства LineStyle, Color, и Marker вместо использования символьной строки. Это может быть полезным, например, если вы хотите задать цвет, которого нет в приведенном выше списке спецификаторов цвета, при помощи тройки значений RGB. Более подробная информация о возможностях выбора цвета дана в разделе ColorSpec.
ПримерыПостроим синусоидальную функцию для трех различных пределов изменения аргумента, используя различные стили линий, цвета и маркеры.
t = 0 : pi/20 : 2*pi;
plot(t, sin(t), '-.r*')
hold on
plot(sin(t - pi/2), '--mo')
plot(sin(t - pi), ':bs')
hold off
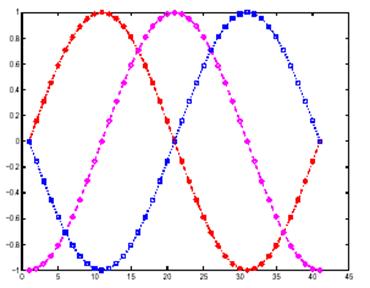
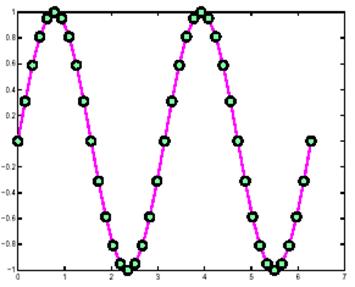
Построим еще один график, иллюстрирующий как можно задавать свойства линий.
plot(t, sin(2*t),'-mo',...
'LineWidth', 2,...
'MarkerEdgeColor', 'k',...
'MarkerFaceColor', [0.49 1 0.63],...
'MarkerSize', 12)
См. также функции:
line, plot, patch, set, surface, и свойство LineStyleOrder координатных осей
[1] Данная терминология не совсем соответствует принятой в русско-язычных изданиях.
Похожие работы
... должны быть прямоугольными. 5. Полиномы По степени применимости, по разнообразию и качеству соответствующих команд скалярные полиномы – следующие за матрицами математические объекты в MATLAB'е. Полином p(x)=anxn+an-1xn-1+...+a0 задается вектором-строкой p из чисел an, an-1, ... , a0, т.е. коэффициентами, расположенными в порядке убывания показателя степени. Его степень n задавать не ...
... классики полезно вспомнить о потенциальном резерве времени, который объективно появляется при использовании систем автоматизации математических расчетов, и использовать этот резерв для резкого расширения круга изучаемых задач и методов вычислений. Незаменима роль системы Derive для интенсификации обучения при подготовке к вступительным экзаменам по математике. Ситуация известна: школьный курс ...
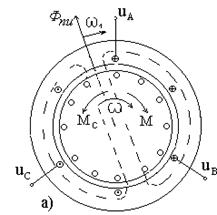
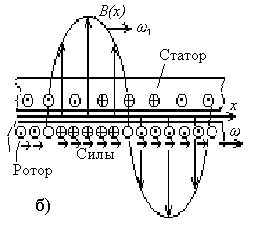
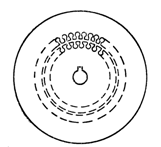
... концентрических окружностей с уменьшающимся радиусом по мере затухания колебаний скорости и момента. Аналогичная картина наблюдается при ступенчатом набросе нагрузки. 5. РАЗРАБОТКА ВИРТУАЛЬНОЙ ЛАБОРАТОРНОЙ РАБОТЫ НА БАЗЕ ВИРТУАЛЬНОЙ АСИНХРОННОЙ МАШИНЫ Иную возможность анализа АД представляет специализированный раздел по электротехнике Toolbox Power System Block. В его библиотеке имеются блоки ...
... Работа с демонстрационными примерами с командной строки Вызов списка демонстрационных примеров Одним из самых эффективных методов знакомства со сложными математическими системами является ознакомление со встроенными примерами их применения. Система MATLAB содержит многие сотни таких примеров – по примеру практически на каждый оператор или функцию. Наиболее поучительные примеры можно найти ...
0 комментариев