Навигация
Визначення та призначення тригерів. Класифікація тригерів
2. Визначення та призначення тригерів. Класифікація тригерів
Тригери - це мікроелектроні схеми з двома стійкими станами. Вони призначені для зберігання значень двійкового розряду цифр 0 або 1.
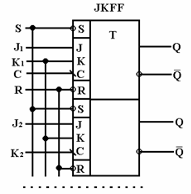
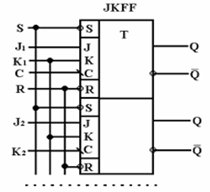
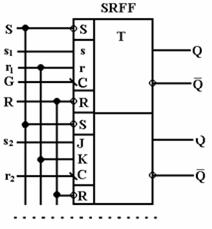
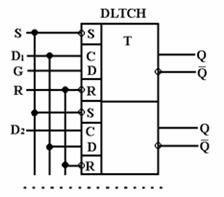
Тригери мають динамічне і потенційне керування. Кожен компонент може містити один чи кілька тригерів у корпусі, у яких загальними є сигнали установки, скидання і тактової синхронізації (дивись малюнок). Перелік тригерів приведений нижче у таблиці.
а)
б)
в)
г)
Мал.- Тригери: а) - JK-тригер з негативним фронтом спрацьовування і низьким рівнем сигналів установки і скидання; б) - D-тригер з позитивним фронтом спрацьовування і низьким рівнем сигналів установки і скидання; в) - синхронний двотактний RS-тригер; г) -синхронний однотактний D-тригер
Таблиця. Перелік тригерів
| Тип | Параметри | Порядок перерахування виводів | Функціональне призначення | |
| Тригери з динамічним керуванням | ||||
| JKFF | Кількість тригерів | S,R,C,J,J,...,K,K,...,Q,Q,..., Q, Q,... | JK-тригер з негативним фронтом спрацьовування і низьким рівнем сигналу установки і скидання | |
| DFF | Кількість тригерів | S, R, C, D, D,..., Q, Q,..., Q, Q,... | D-тригер з позитивним фронтом спрацьовування і низьким рівнем сигналу установки і скидання | |
| Тригери з потенційним управлінням | ||||
| SRFF | Кількість тригерів | S, R, G, S, S,..., R, R,...,Q,Q,..., Q,Q,... | Двотактний синхронний RS‑тригер | |
| DLTCH | Кількість тригерів | S,R,G,D,D,..., Q, Q,..., Q, Q,... | Однотактний синхронний D‑тригер | |
Моделі динаміки тригерів з динамічним керуванням мають формат:
MODEL <ім'я моделі> UEFF [(параметри)]
Параметри моделі тригерів з динамічним керуванням типу UEFF приведені нижче в таблиці (значення за замовчуванням - 0, одиниця виміру - c). Коса риса "/" означає "чи"; наприклад, запис S/R означає сигнал S чи R.
Моделі динаміки тригерів з потенційним керуванням має формат:
MODEL <ім'я моделі> UGFF [(параметри)]
Параметри моделі тригерів з потенційним керуванням типу UGFF приведені в таблиці 5 (значення за замовчуванням - 0, одиниця виміру ‑ с).
За замовчуванням у початковий момент часу вихідні стани тригерів прийняті невизначеними (стани X). Вони залишаються такими до подачі сигналів чи установки чи скидання переходу тригера у визначений стан. У МС5 мається можливість установити визначений початковий стан за допомогою параметра DIGINITSTATE діалогового вікна Global Settings.
У моделях тригерів маються параметри, що характеризують мінімальні тривалості сигналів установки і скидання і мінімальну тривалість імпульсів. Якщо ці параметри більше нуля, то в процесі моделювання обмірювані значення длительностей імпульсів порівнюються з заданими даними і при наявності занадто коротких імпульсів на екран видаються попереджуючі повідомлення.
Завдання №1
1. Перевести 121,37 з десяткової системи числення у двійкову: 121,3710=1111001,01012
| 121 | 2 | 0,37 | |||||||||
| 120 | 60 | 2 | 2 | ||||||||
| 1 | 60 | 30 | 2 | 0,74 | |||||||
|
| 0 | 30 | 15 | 2 | 2 | ||||||
| 0 | 14 | 7 | 2 | 1,48 | |||||||
| 1 | 6 | 3 | 2 | 2 | |||||||
| 1 | 2 | 1 | 2 | 0,96 | |||||||
| 1 | 0 | 0 | 2 | ||||||||
| 1 | 1,92 |
вісімкову: 121,3710=171,27538
| 121 | 8 | 0,37 | |||||
| 120 | 15 | 8 | 8 | ||||
| 1 | 8 | 1 | 8 | 2,96 | |||
|
| 7 | 0 | 0 | 8 | |||
| 1 | 7,68 | ||||||
| 8 | |||||||
| 5,44 | |||||||
| 8 | |||||||
| 3,52 |
шістнадцяткову: 121,3710=79,5ЕВ816
| 121 | 16 | 0,37 | |||||
| 112 | 7 | 16 | 16 | ||||
| 9 | 0 | 0 | 5,92 | ||||
|
| 7 | 16 | |||||
| 14,72 | |||||||
| 16 | |||||||
| 11,52 | |||||||
| 16 | |||||||
| 8,32 |
двійково-десяткову: 121,3710=1 0010 0001,0011 01112-10
2. Перевести з двійкової системи числення у десяткову:
110111002=1·27+1·26+0·25+1·24+1·23+1·22+0·21+0·20= +1·128+1·64+0·32+1·16+1·8+1·4+0·2+0·1=128+64+0+16+8+4+0+0=22010
вісімкову: 110111002=011 011 1002=3348
шістнадцяткову: 110111002=1101 11002=DC16
Завдання №2
1. записати всі константи одиниці;
2. записати всі константи нуля;
3. записати досконалу диз’юнктивну нормальну форму;
4. записати досконалу кон’юктивну нормальну форму;
5. мінімізувати функцію за допомогою карт Карно;
6. побудувати комбінаційну схему заданої функції у базисі "І-ЧИ-НЕ"
| Х1 | Х2 | Х3 | Х4 | f | константа 1 | константа 0 |
| 0 | 0 | 0 | 0 | 1 | x1x2x3x4 |
|
| 0 | 0 | 0 | 1 | 1 | x1x2x3x4 |
|
| 0 | 0 | 1 | 0 | 1 | x1x2x3x4 |
|
| 0 | 0 | 1 | 1 | 1 | x1x2x3x4 |
|
| 0 | 1 | 0 | 0 | 0 |
| x1Úx2Úx3Úx4 |
| 0 | 1 | 0 | 1 | 0 |
| x1Úx2Úx3Úx4 |
| 0 | 1 | 1 | 0 | 0 |
| x1Úx2Úx3Úx4 |
| 0 | 1 | 1 | 1 | 1 | x1x2x3x4 |
|
| 1 | 0 | 0 | 0 | 1 | x1x2x3x4 |
|
| 1 | 0 | 0 | 1 | 1 | x1x2x3x4 |
|
| 1 | 0 | 1 | 0 | 0 |
| x1Úx2Úx3Úx4 |
| 1 | 0 | 1 | 1 | 1 | x1x2x3x4 |
|
| 1 | 1 | 0 | 0 | 0 |
| x1Úx2Úx3Úx4 |
| 1 | 1 | 0 | 1 | 1 | x1x2x3x4 |
|
| 1 | 1 | 1 | 0 | 0 |
| x1Úx2Úx3Úx4 |
| 1 | 1 | 1 | 1 | 1 | x1x2x3x4 |
|
ДДНФ: F = x1x2x3x4 Ú x1x2x3x4 Ú x1x2x3x4 Ú x1x2x3x4 Ú x1x2x3x4 Ú Ú x1x2x3x4 Ú x1x2x3x4 Ú x1x2x3x4 Ú x1x2x3x4 Ú x1x2x3x4
ДДКНФ: F = (x1Úx2Úx3Úx4)Ù(x1Úx2Úx3Úx4)Ù(x1Úx2Úx3Úx4)Ù Ù(x1Úx2Úx3Úx4)Ù(x1Úx2Úx3Úx4)Ù(x1Úx2Úx3Úx4)
|
|
| 01 | 11 | 10 | ||
| 00 | 1 | 1 | 1 | 1 | ||
| 01 | 1 | |||||
| 11 | 1 | 1 | ||||
| 10 | 1 | 1 | 1 |
МДНФ: F = x1x2 Ú x3x4 Ú x1x3x4 Ú x1x2x3
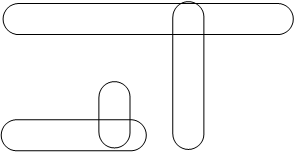
Комбінаційна схема:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() x1
x1
![]()
![]()
![]()
![]() x2
x2
![]()
![]()
![]() x3
x3
![]()
![]() x4
x4
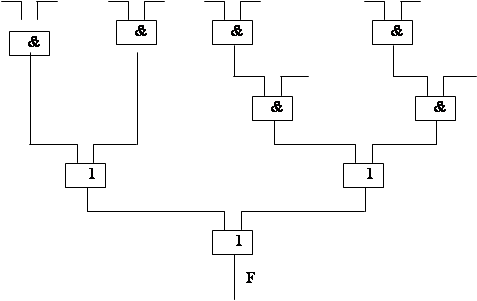 | |||||
Список використаної літератури
1. "Комп’ютерна схемотехніка". М.П.Бабич, І.А.Жуков. МК-Прес. 2004 рік.
2. Конспект лекцій.
3. Інтернет.
Похожие работы
... в іншу (найчастіше для переведення із двійкової, вісімкової та шістнадцяткової систем числення у десяткову, і навпаки). 6. Програмна реалізація Програма розроблена для перетворення чисел з однієї системи числення в іншу.Реалізована в середовищі програмування Borland C++Builder. Лістінг програми: #include <vcl.h> #pragma hdrstop #include "Unit1.h" #include <math.h> #include < ...
... файл Kurs2.exe і далі використовувати головне меню програми. Висновки Завершивши роботу над курсовим проектом можна зробити висновок про те, що мені вдалося досягти своєї мети і розробити програму переводу з однієї системи числення у іншу. За допомогою засобів алгоритмічної мови Turbo Pascal було створено програму Kurs2‚ яка дозволяє здійснювати перевід чисел з двійкової‚ вісімкової та ші ...
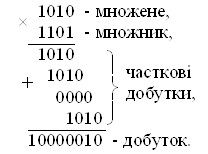
... ї довжини послідовності чи нулів одиниць, що приводить до необхідності одночасного аналізу декількох розрядів множника і зрушенню на довільне число розрядів. 3.3.3. Апаратні методи прискорення операції множення в двійковій системі числення Спочатку розглянемо апаратні методі прискорення операції множення першого порядку. 1. Метод множення з перетворенням цифр множнику групування розрядiв і ...
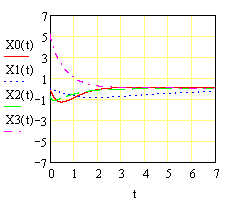
... мы будем определять аналитические зависимости изменения переменных состояния системы численными методами с использованием переходной матрицы, а также с помощью специальных функций MATHCAD. 2.2 Теоретическое обоснование применения преобразования Лапласа Классический метод решения системы дифференциальных уравнений высокого порядка связан с большими вычислительными затратами, особенно при ...
 00
00

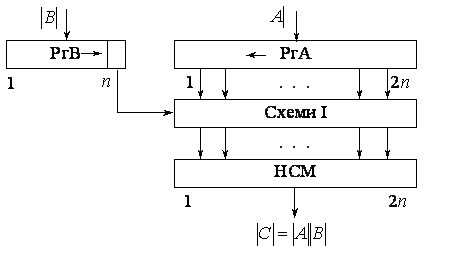


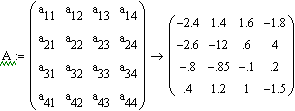
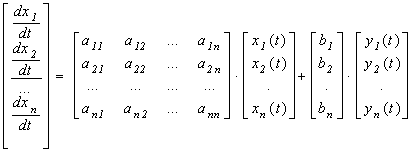
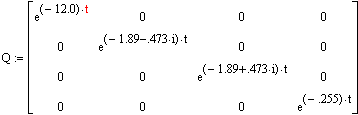
0 комментариев