Навигация
Двухфазные системы массового обслуживания с ожиданием
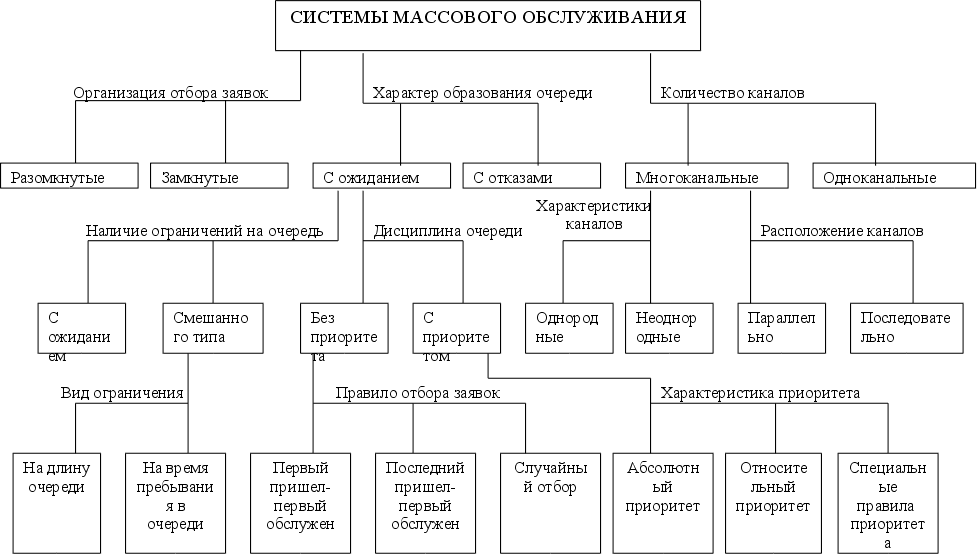
2.2 Двухфазные системы массового обслуживания с ожиданием
Примером двухфазной системы массового обслуживания с ожиданием могут служить магазины, в которых, прежде чем получить товар, покупатель должен оплатить его стоимость в кассе. Этот пример является типичным, но не единственным в своем роде. Работа подобных систем массового обслуживания будет рассмотрена на примерах двухфазных одноканальных систем массового обслуживания с неограниченным и ограниченным потоком заявок.
2.3 Системы с неограниченным потоком заявок
Рассматривается работа системы массового обслуживания, состоящая из двух приборов разной производительности.
Время обслуживания приборами заявок подчинено показательному закону распределения с параметрами ![]() и
и ![]() соответственно для первого и второго приборов. Поступившее в систему требование вначале обслуживается первым прибором. Если он уже занят, то требование ожидает своей очереди до тех пор, пока все ранее пришедшие требования не будут обслужены. После обслуживания первым прибором требования поступают на второй. Так же как и в предыдущем приборе, они поступают на обслуживание, если второй прибор свободен. Если прибор занят, то требование становится в очередь. Для неограниченного пуассоновского входящего потока с плотностью
соответственно для первого и второго приборов. Поступившее в систему требование вначале обслуживается первым прибором. Если он уже занят, то требование ожидает своей очереди до тех пор, пока все ранее пришедшие требования не будут обслужены. После обслуживания первым прибором требования поступают на второй. Так же как и в предыдущем приборе, они поступают на обслуживание, если второй прибор свободен. Если прибор занят, то требование становится в очередь. Для неограниченного пуассоновского входящего потока с плотностью ![]() можно написать уравнения состояний системы:
можно написать уравнения состояний системы:
 (1)
(1)
где ![]() - вероятность того, что в момент времени t оба прибора свободны;
- вероятность того, что в момент времени t оба прибора свободны;
![]() - вероятность состояния системы, при котором в момент времени t в первой фазе находится
- вероятность состояния системы, при котором в момент времени t в первой фазе находится ![]() требований (включая и те, которые обслуживаются), а во второй фазе -
требований (включая и те, которые обслуживаются), а во второй фазе - ![]() требований.
требований.
После решения уравнений получены характеристики, описывающие состояния системы массового обслуживания:
1. Вероятность того, что оба прибора (обе фазы) свободны от заявок:
![]() где
где ![]()
2. Вероятность того, что в первой фазе находится одна заявка, а во второй ни одной:
![]()
3. Вероятность того, что во второй фазе имеется одна заявка, а в первой ни одной:
![]()
4. Вероятность того, что в первой фазе находится одна заявка, и во второй фазе тоже одна заявка:
![]()
5. Математическое ожидание числа заявок, находящихся в системе:
![]()
при этом среднее число заявок, находящихся в первой фазе, равно:
![]() ,
,
а во второй фазе:
![]() , где
, где ![]()
3. Выполнение задания
Введем несколько формул:
1. среднее время ожидания заявки в очереди: ![]()
2. среднее время пребывания заявки в системе: ![]()
3. среднее число заявок в системе: ![]()
где ![]() - среднее число заявок в очереди и
- среднее число заявок в очереди и 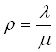 .
.
Учитывая, что произвольная заявка, поступившая в систему в момент обслуживания, застает ее занятой с вероятностью R, можно записать:
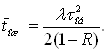 (2)
(2)
Отсюда следует, что
![]()
Так как имеется 2 фазы то:
![]() , (3)
, (3)
с использованием соответственно ![]() для каждой их фаз.
для каждой их фаз.
Произведем вычисления для неэкспоненциального распределения, причем средние длительности обслуживания в обоих случаях равны.
Если выразить второй начальный момент через дисперсию, математическое ожидание и коэффициент вариации, то
 ,
,
где ![]() - коэффициент вариации, характеристика, показывающая степень нерегулярности потока заявок. Тогда среднее время ожидания
- коэффициент вариации, характеристика, показывающая степень нерегулярности потока заявок. Тогда среднее время ожидания
 (4)
(4)
Выражение (4) используем, чтобы найти среднее время ожидания заявки во второй фазе, для первой же фазы используем выражение (2). Затем по формуле (3) находим среднее время пребывания заявки в системе.
Производим сравнение полученных результатов при экспоненциальном распределении и неэкспоненциальном распределении.
4. Программа
//---------------------------------------------------------------------------
#pragma hdrstop
#include <iostream.h>
#include <string.h>
#include <conio.h>
//---------------------------------------------------------------------------
#pragma argsused
int main(int argc, char* argv[])
{
float a1,a2,ly=5,T1=0.15,T2=0.14,M1,M2,M,P00,P10,P01,P11;
a1=ly*T1;
a2=ly*T2;
P00=(1-a1)*(1-a2);//обе фазы свободны от заявок
P10=a1*(1-a1)*(1-a2);//в 1-й фазе заявка,2-я свободна
P01=a2*(1-a1)*(1-a2);//в 2-й фазе заявка,1-я свободна
P11=a1*a2*(1-a1)*(1-a2);//обе фазы заняты
M1=a1/(1-a1);//среднее число заявок,находящихся в 1-й фазе
M2=a2/(1-a2);//среднее число заявок,находящихся в 2-й фазе
M=M1+M2;//Математическое ожидание числа заявок,находящихся в системе
cout<<'\n'<<"P00= "<<P00<<'\n'<<"P10= "<<P10<<'\n'<<"P01= "<<P01<<'\n'<<"P11= "<<P11<<'\n'<<"M1= "<<M1<<'\n'<<"M2= "<<M2<<'\n'<<"M= "<<M;
float toz1,toz2,tpreb1,tpreb2;//для экспон. и неэкспон. распределения соответственно
float R1,R2,k1=0.7,k2=0.8,k3=0.9;
R1=P10+P11;R2=P01+P11;
toz1=ly*(T1*T1/(2-2*R1)+T2*T2/(2-2*R2));
toz2=ly*(T1*T1/(2-2*R1)+T1*T1*(1+k1*k1+k2*k2+k3*k3)/(2-2*R2));
tpreb1=toz1+(a1+a2)/ly;
tpreb2=toz2+(a1+a2)/ly;
cout<<'\n'<<"Srednee vremya ozidania zaavki v system pri eksponencialnom raspredelenii: "<<'\n'<<toz1<<'\n'<<"Srednee vremya ozidania zaavki v system pri neeksponencialnom raspredelenii: "<<'\n'<<toz2<<'\n'<<"Sravnenie: "<<'\n'<<toz2/toz1<<'\n';
cout<<'\n'<<"Srednee vremya prebivania zaavki v system pri eksponencialnom raspredelenii: "<<'\n'<<tpreb1<<'\n'<<"Srednee vremya prebivania zaavki v system pri neeksponencialnom raspredelenii: "<<'\n'<<tpreb2<<'\n'<<"Sravnenie: "<<'\n'<<tpreb2/tpreb1<<'\n';
getch();
return 0;
}
//---------------------------------------------------------------------------
5. Результаты

Для заданных значений имеем:
1. значения характеристик, описывающих состояния системы массового обслуживания;
2. значения среднего времени ожидания заявки в системе при экспоненциальном и неэкспоненциальном распределении времени обслуживания для сравнения;
3. значения среднего времени пребывания заявки в системе при экспоненциальном и неэкспоненциальном распределении времени обслуживания для сравнения.
При сравнении мы видим, что при неэкспоненциальном распределении времени обслуживания среднее время ожидания заявки увеличилось в 2,1 раз по сравнению с экспоненциальным, а среднее время пребывания в системе примерно в 1,3 раз.
Следовательно, производительность при заданных значениях выше при экспоненциальном распределении времени обслуживания по сравнению с неэкспоненциальным.
Литература
1. Новиков О.А., Петухов С.И. Прикладные вопросы теории массового обслуживания. М., Изд-во "Советское радио", 1969.
Похожие работы
... 2-3 Поиск литературы 7 1 7 2-4 Разработка модели разветвленной СМО 6 1 6 3 Поиск литературы завершен 3-6 Изучение литературы по теории массового обслуживания 10 1 10 4 Модель разработана 4-5 Разработка алгоритма программы 10 1 10 5 Алгоритм программы разработан 5-7 Выбор среды программиро-вания и создание программы 30 1 ...
... ;0 – постоянная. Плотность распределения показательного закона задается формулой: где 2>0, - интенсивность поступления заявок 2-го потока. Необходимо также учесть, что моделируемая система массового обслуживания является СМО с отказами и с абсолютным приоритетом. Т.е. заявки 1 имеют перед заявками 2 приоритет, состоящий в том, что если заявка 1 приходит в систему, когда все каналы ...
... как точки на временной оси. Для достижения основной цели моделирования достаточно наблюдать систему в моменты реализации основных событий. Рассмотрим пример одноканальной системы массового обслуживания. Целью имитационного моделирования подобной системы является определение оценок ее основных характеристик, таких, как среднее время пребывания заявки в очереди, средняя длина очереди и доля ...
... техники на 2000 рублей в день. Это позволит получить прибыль 1779337 рублей в месяц. ЗАКЛЮЧЕНИЕ В данном курсовом проекте представлена тема "Математическое моделирование и оптимизация системы массового обслуживания". Системы массового обслуживания имеют огромное практическое применение в наше время, что показано в рассмотренном примере. Целью данного курсового проекта было определение - ...
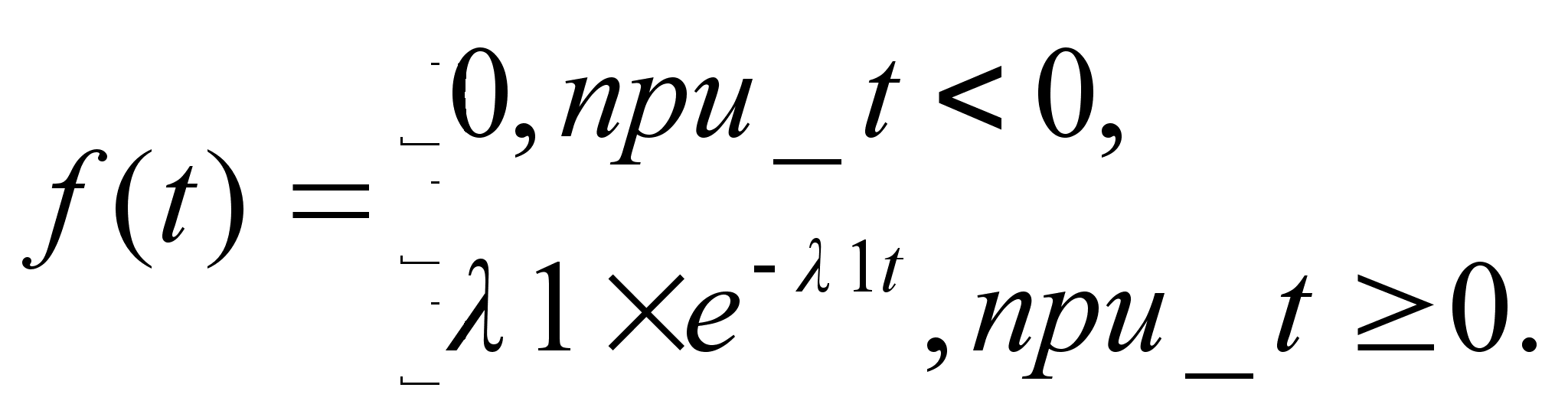
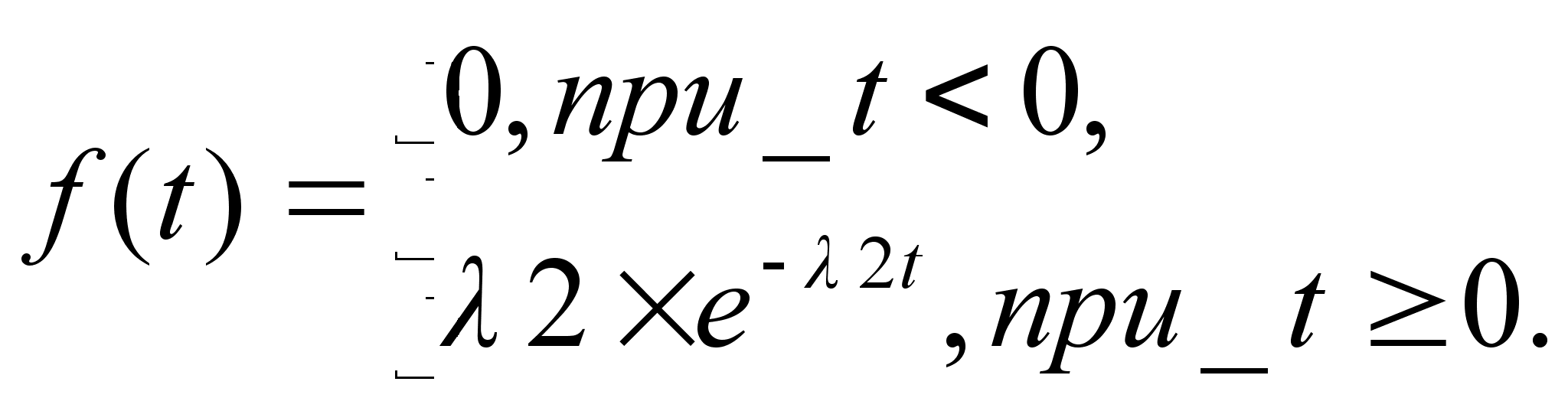
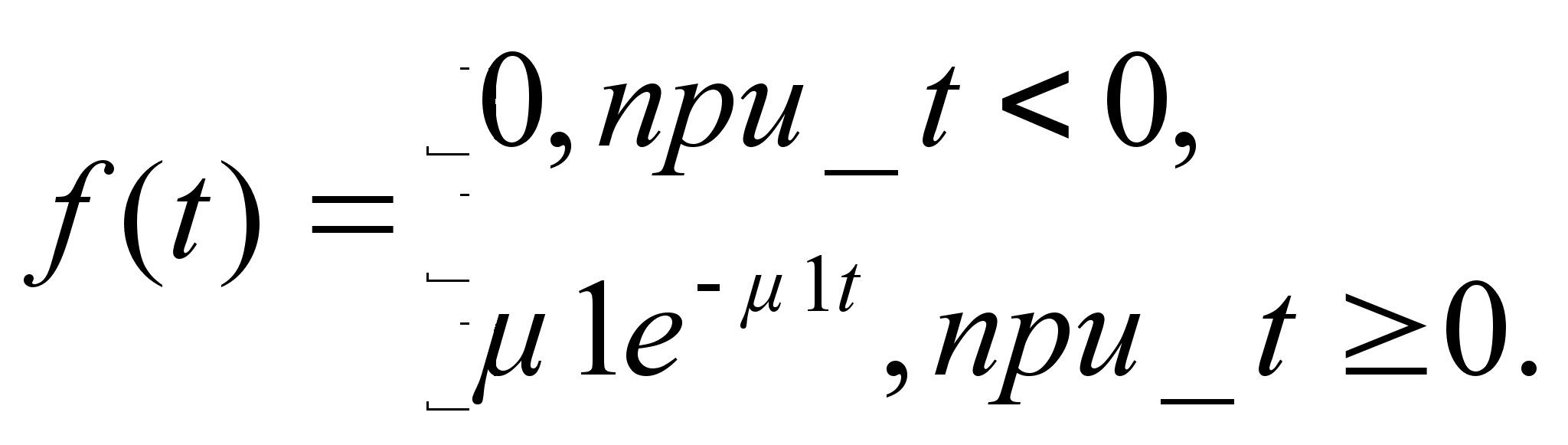
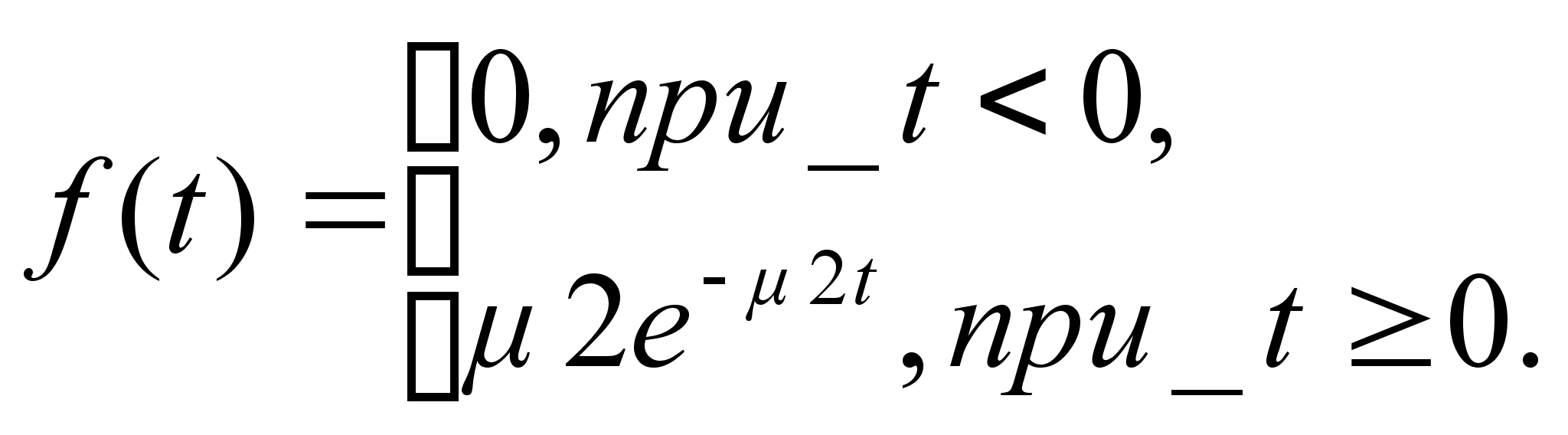
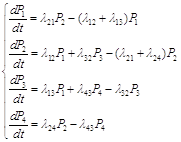

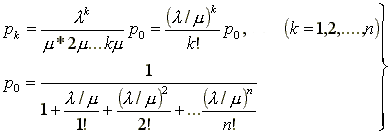
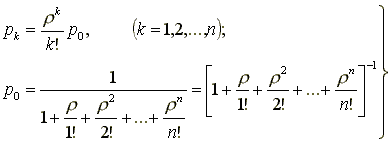

0 комментариев