Навигация
Моделирование 2-х канальной системы массового обслуживания с отказами
Содержание.
| Введение. | 2 |
| 1. Теория массового обслуживания. | 3 |
| 1.1.Предмет и задачи теории массового обслуживания. | 3 |
| 1.2. Система массового обслуживания (СМО). | 3 |
| 1.3. Классификация СМО. | 3 |
| 1.4. Характеристики СМО. | 5 |
| 2. Постановка задачи на проектирование. | 5 |
| 2.1. Формулировка задачи. | 5 |
| 2.2. Теоретическое представление задачи | 5 |
| 3.Решение задачи. | 7 |
| 3.1. Алгоритм моделирования СМО | 7 |
| 4. Программная реализация. | 8 |
| 5. Выводы. | 9 |
| Заключение. | 10 |
| Приложение 1. Результаты работы СМО. | 11 |
| Приложение 2. График зависимость абсолютной пропускной способности системы от времени. Зависимость абсолютной пропускной способности системы от времени. | 12 |
| Приложение 3. График зависимость относительной пропускной способности системы от времени. | 12 |
| Приложение4. График зависимости вероятности отказа системы от времени. | 13 |
| Приложение 5. График зависимости количества поступивших и обслуженных заявок в системе от времени. | 13 |
| Приложение 6. Листинг программы. | 14 |
| Приложение 7. Блок-схемы. | |
| Список литературы. | 16 |
Введение.
За последнее время в самых разных областях практики возникла необходимость в решении различных вероятностных задач, связанных с работой так называемых систем массового обслуживания (СМО). Примерами таких систем могут служить: телефонные станции, ремонтные мастерские, билетные кассы, стоянки такси, парикмахерские и т.п.
Темой данного курсового проекта как раз и является решение подобной задачи. Однако, в предложенной задаче будет исследована СМО, в которой рассматриваются 2 потока заявок, один из которых обладает приоритетом. Также рассматриваемые процессы являются немарковскими, т. к. важен фактор времени. Поэтому решение данной задачи построено не на аналитическом описании системы, а на статистическом моделировании.
Практическое решение задачи осуществлено с помощью программы, реализованной в среде TURBO PASCKAL.
Теория массового обслуживания. Основные положения.1.1. Предмет и задачи теории массового обслуживания.
Теория массового обслуживания опирается на теорию вероятностей и математическую статистику.
На первичное развитие теории массового обслуживания оказали особое влияние работы датского ученого А.К. Эрланга (1878-1929).
Теория массового обслуживания – область прикладной математики, занимающаяся анализом процессов в системах производства, обслуживания, управления, в которых однородные события повторяются многократно, например, на предприятиях бытового обслуживания; в системах приема, переработки и передачи информации; автоматических линиях производства и др.
Предметом теории массового обслуживания является установление зависимостей между характером потока заявок, числом каналов обслуживан6ия, производительностью отдельного канала и эффективным обслуживанием с целью нахождения наилучших путей управления этими процессами.
Задача теории массового обслуживания – установить зависимость результирующих показателей работы системы массового обслуживания (вероятности того, что заявка будет обслужена; математического ожидания числа обслуженных заявок и т.д.) от входных показателей (количества каналов в системе, параметров входящего потока заявок и т.д.). Результирующими показателями или интересующими нас характеристиками СМО являются – показатели эффективности СМО, которые описывают способна ли данная система справляться с потоком заявок.
Задачи теории массового обслуживания носят оптимизационный характер и в конечном итоге включают экономический аспект по определению такого варианта системы, при котором будет обеспечен минимум суммарных затрат от ожидания обслуживания, потерь времени и ресурсов на обслуживание и простоев каналов обслуживания.
1.2. Система массового обслуживания.
Система обслуживания считается заданной, если известны:
1) поток требований, его характер;
2) множество обслуживающих приборов;
3) дисциплина обслуживания (совокупность правил, задающих процесс обслуживания).
Каждая СМО состоит из какого-то числа обслуживающих единиц, которые называются каналами обслуживания. В качестве каналов могут фигурировать: линии связи, различные приборы, лица, выполняющие те или иные операции и т.п
Всякая СМО предназначена для обслуживания какого-то потока заявок, поступающих в какие-то случайные моменты времени. Обслуживание заявок продолжается какое-то случайное время, после чего канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времен обслуживания приводит к тому, что в какие-то периоды времени на входе СМО скапливается излишне большое число заявок (они либо становятся в очередь, либо покидают СМО не обслуженными); в другие же периоды СМО будет работать с недогрузкой или вообще простаивать.
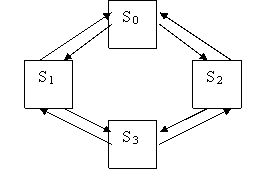
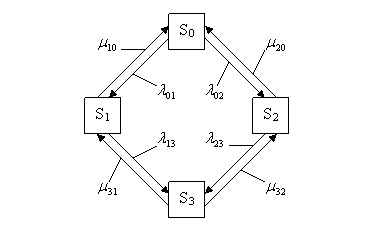
Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем; состояние СМО меняется скачком в моменты появления каких-то событий ( или прихода новой заявки, или окончания обслуживания, или момента, когда заявка, которой надоело ждать, покидает очередь ).
Похожие работы
... техники на 2000 рублей в день. Это позволит получить прибыль 1779337 рублей в месяц. ЗАКЛЮЧЕНИЕ В данном курсовом проекте представлена тема "Математическое моделирование и оптимизация системы массового обслуживания". Системы массового обслуживания имеют огромное практическое применение в наше время, что показано в рассмотренном примере. Целью данного курсового проекта было определение - ...
... сколько их уже исправно и ждет наладки. Классификация СМО далеко не ограничивается приведенными разновидностями, но этого достаточно.2. Системы массового обслуживания с ожиданием 2.1 Одноканальная СМО с ожиданием Рассмотрим простейшую СМО с ожиданием — одноканальную систему (n - 1), в которую поступает поток заявок с интенсивностью ; интенсивность обслуживания (т.е. в среднем непрерывно ...
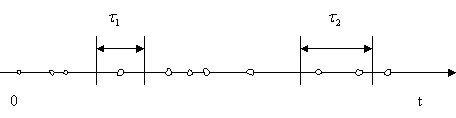
... как точки на временной оси. Для достижения основной цели моделирования достаточно наблюдать систему в моменты реализации основных событий. Рассмотрим пример одноканальной системы массового обслуживания. Целью имитационного моделирования подобной системы является определение оценок ее основных характеристик, таких, как среднее время пребывания заявки в очереди, средняя длина очереди и доля ...
... 2-3 Поиск литературы 7 1 7 2-4 Разработка модели разветвленной СМО 6 1 6 3 Поиск литературы завершен 3-6 Изучение литературы по теории массового обслуживания 10 1 10 4 Модель разработана 4-5 Разработка алгоритма программы 10 1 10 5 Алгоритм программы разработан 5-7 Выбор среды программиро-вания и создание программы 30 1 ...
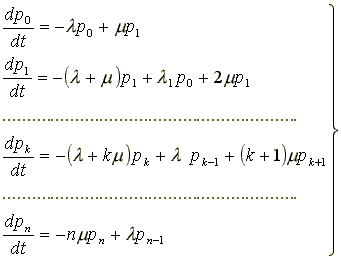


0 комментариев