Навигация
Функциональное и логическое программирование
СОДЕРЖАНИЕ
Введение
1 Постановка задачи
2 Математические и алгоритмические основы решения задачи
3 Функциональные модели и блок-схемы решения задачи
4 Программная реализация решения задачи
5 Пример выполнения программы
Заключение
Список использованных источников и литературы
ВВЕДЕНИЕ
Функция – это термин, используемый в математике для обозначения такой зависимости между двумя величинами, при которой если одна величина задана, то другая может быть найдена.
Обычно функция (с 17 в.) задается формулой, выражающей зависимую переменную через одну или несколько независимых переменных. Например, площадь круга есть функция его радиуса, и эта зависимость записывается формулой A = pr2; периметр прямоугольника является функцией его длины и ширины или P = 2(l + w). Функцию можно изобразить графически, нанося точки, координатами которых служат независимые и зависимые переменные, на координатную плоскость (рисунок 1).
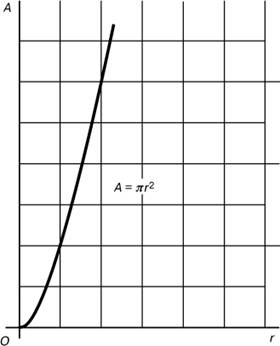
Рисунок 1. График функции A = pr2 (площадь круга как функция радиуса).
Считалось, что график, подобный изображенному на рис. 2, не может быть графиком одной функции, так как различные его части должны описываться различными формулами (y = x для x от 0 до 1; y = –x для x от 1 до 0; y = 2 – x для x от 1 до 2 и т.д.). Каково же было удивление математиков, когда в начале 19 в. они обнаружили, что график функции, изображенной на рисунке 2, в действительности определяется формулой
![]() ,
,
где многоточие указывает на то, что формула неограниченно продолжается аналогичным образом.
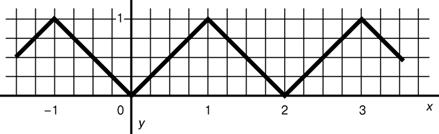
Рисунок 2. График функции, представимой в виде бесконечного ряда.
Это открытие привело к пересмотру определения функции. Согласно новому определению, под функцией надлежит понимать любое правило, позволяющее находить одно число (значение зависимой переменной), если задано другое число или набор чисел (значений независимых переменных). Такое правило может быть выражено формулой, но это необязательно.
В настоящее время такое определение функции заменено более общим. Определение функции как правила, ставящего в соответствие значение зависимой переменной каждому значению независимой переменной, не удовлетворяло, поскольку не определяло функцию как математический объект.
Функции делятся на элементарные и неэлементарные.
Целью данной курсовой работы является ЛИСП-реализация вычисления неэлементарных функций.
1. Постановка задачи
Требуется реализовать вычисление неэлементарных функций.
Рассмотрим примеры неэлементарных функций и способов их вычисления:
1) гамма-функция Эйлера
G(x) =![]() ,
,
при положительном целом x:
Г (n) = (n - 1)! = 1·2... (n - 1).
Для x>0 гамма-функция получается из ее логарифма взятием экспоненты.
![]() .
.
2) ![]() ;
;
3) 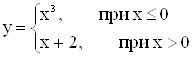 ;
;
4) 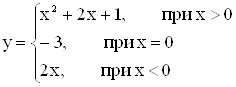 .
.
Пример 1.
Вычислить гамма-функции Г(5).
Решение:
Так как 5 – положительное целое число:
Г(5) =(5-1)! =4! = 24.
Ответ: 24.
Пример 2.
Вычислить гамма-функции Г(0.5).
Решение:
Воспользуемся формулой вычисления гамма функции для положительных x:
![]() .
.
![]() .
.
Ответ: ![]() .
.
Пример 3.
Вычислить функцию ![]() при x=-5.
при x=-5.
Решение:
![]() .
.
Ответ: 5.
Пример 4.
Вычислить функцию 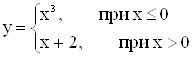 , при x=-2.
, при x=-2.
Решение:
Так как -2 < 0, следовательно
![]() .
.
Ответ: -8.
Пример 5.
Вычислить функцию 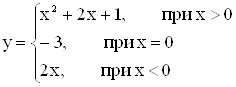 , при x=4.
, при x=4.
Решение:
Так как 4 > 0, следовательно
![]() .
.
Ответ: 25.
Похожие работы
... . В частности: (8) Из (7) и (8) следует, что в M нет двух неравных натуральных чисел. Доказательство закончено. 3.2 Рекурсия Особое место для систем функционального программирования приобретает рекурсия, поскольку она позволяет учитывать значения функции на предыдущих шагах. С теоретической точки зрения рекурсивные определения являются теоретической основой всей современной ...
... По теореме 9.3 в силу результатов шагов 3 и 8. (Шаг 10). Имеет место свойство (9.4) по теореме 9.5 в силу результатов шагов 1 и 9. Литература к лекции 9. 9.1. С.А. Абрамов. Элементы программирования. - М.: Наука, 1982. С. 85-94. 9.2. М. Зелковец, А. Шоу, Дж. Гэннон. Принципы разработки программного обеспечения. - М.: Мир, 1982. С. 98-105. Лекция 10. ТЕСТИРОВАНИЕ И ОТЛАДКА ПРОГРАММНОГО ...
... проектирование и программирование 0.8 Структурное проектирование включает в себя: - нисходящее проектирование ("сверху вниз"), - модульное программирование, - структурное программирование. 0.8.1.Нисходящее проектирование Метод предполагает последовательное разложение функции обработки данных на простые функциональные элементы ("сверху ...
... . Объясните, для чего служат разрешения и привилегии в Windows NT. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету СИСТЕМНОЕ ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ Билет № 22 Перечислите возможности и инструменты системы программирования Microsoft Developer Studio. Укажите для чего предназначается буфер в системах ввода-вывода, ...

0 комментариев