Навигация
Программная реализация решения задачи
4 Программная реализация решения задачи
;ФУНКЦИЯ Y=|X|
(DEFUN ABS_FUNCTION (X)
(ABS X)
)
;ФУНКЦИЯ Y=X^3 ПРИ X<=0 И Y=X+2 ПРИ X>0
(DEFUN FUNCTION1 (X)
(IF (<= X 0)
(* X X X)
(+ X 2)
)
)
;ФУНКЦИЯ Y=X^2+2X+1 ПРИ X>0, Y=-3 ПРИ X=0, Y=2X ПРИ X<0
(DEFUN FUNCTION2 (X)
(COND
((> X 0) (+ (* X X) (* 2 X) 1))
((= X 0) -3)
((< X 0) (* 2 X))
)
)
;ФУНКЦИЯ РЕАЛИЗУЮЩАЯ ФАКТОРИЛ X
(DEFUN FACTORIAL (X)
(COND
((EQL X 0) 1)
((EQL X 1) 1)
(T (* X (FACTORIAL (- X 1))))
)
)
;ГАММА ДЛЯ ЦЕЛЫХ ПОЛОЖИТЕЛЬНЫХ ЧИСЕЛ
(DEFUN GAMMA_INT (X)
(FACTORIAL (- X 1))
)
;ВЫЧИСЛЕНИЕ ГАММА ФУНКЦИИ ДЛЯ ЛЮБЫХ X
(DEFUN GAMMA_ALL_X (X)
(DECLARE (SPECIAL Y))
(DECLARE (SPECIAL GAM))
(DECLARE (SPECIAL J))
(DECLARE (SPECIAL RES))
(IF (> X 0)
(PROGN
(SETQ Y (+ X 2))
(SETQ GAM (* (SQRT (* 2 (/ PI Y))) (EXP (+ (* Y (LOG Y)) (- (/ (- 1 (/ 1 (* 30 Y Y))) (* 12 Y)) Y)))))
(SETQ RES (/ GAM (* X (+ X 1))))
)
;ИНАЧЕ
(PROGN
(SETQ J 0)
(SETQ Y X)
(DO
(())
((>= Y 0))
(SETQ J (+ J 1))
(SETQ Y (+ Y 1))
)
(SETQ GAM (GAMMA_ALL_X Y))
(DO
((I 0))
((>= I (- J 1)))
(SETQ GAM (/ GAM (+ X I)))
(SETQ I (+ I 1))
)
(SETQ RES GAM)
)
)
RES
)
;ЛОГАРИФМ ГАММА ФУНКЦИИ
(DEFUN GAMMA_LN (X)
(DECLARE (SPECIAL SER))
(DECLARE (SPECIAL L))
(DECLARE (SPECIAL CN))
(DECLARE (SPECIAL Y))
(DECLARE (SPECIAL CO))
;МАССИВ КОЭФФИЦИЕНТОВ
(SETQ CN '(2.5066282746310005 1.0000000000190015 76.18009172947146 -86.50532032941677 24.01409824083091
-1.231739572450155 0.1208650973866179e-2 -0.5395239384953e-5))
(SETQ SER (CADR CN))
(SETQ L (CDDR CN))
(SETQ Y X)
(DO
((J 2))
((>= J 8))
(SETQ Y (+ Y 1))
(SETQ CO (CAR L))
(SETQ SER (+ SER (/ CO Y)))
(SETQ L (CDR L))
(SETQ J (+ J 1))
)
(SETQ Y (+ X 5.5))
(SETQ Y (- Y (* (+ X 0.5) (LOG Y))))
(SETQ Y (+ (* -1 Y) (LOG (* (CAR CN) (/ SER X)))))
)
;ВЫЧИСЛЕНИЕ ГАММА-ФУНКЦИИ ЧЕРЕЗ ЕЕ ЛОГАРИФМ
;ДЛЯ НЕЦЕЛЫХ ПОЛОЖИТЕЛЬНЫХ X
(DEFUN GAMMA_LN_X (X)
(EXP (GAMMA_LN X))
)
;ВЫЧИСЛЕНИЕ ГАММА ФУНКЦИИ
(DEFUN GAMMA (X)
(COND
((= X 0) 0)
;ЦЕЛОЕ ПОЛОЖИТЕЛЬНОЕ
((AND (> X 0) (= (- X (FLOOR X)) 0)) (GAMMA_INT X))
;НЕ ЦЕЛОЕ ПОЛОЖИТЕЛЬНОЕ
((AND (> X 0) (/= (- X (FLOOR X)) 0)) (GAMMA_LN_X X))
;ИНАЧЕ 0
(T (GAMMA_ALL_X X))
)
)
;РАССЧИТЫВАЕМ НЕЭЛЕМЕНТАРНЫЕ ФУНКЦИИ ДЛЯ X
(DEFUN PRINT_RESULT (X)
(PRINT 'X OUTPUT_STREAM)
(PRINT X OUTPUT_STREAM)
(PRINT "Y=|X|" OUTPUT_STREAM)
(PRINT (ABS_FUNCTION X) OUTPUT_STREAM)
(PRINT "Y=X^3 IF X<=0 AND Y=X+2 IF X>0" OUTPUT_STREAM)
(PRINT (FUNCTION1 X) OUTPUT_STREAM)
(PRINT "Y=X^2+2X+1 IF X>0, Y=-3 IF X=0, Y=2X IF X<0" OUTPUT_STREAM)
(PRINT (FUNCTION2 X) OUTPUT_STREAM)
(PRINT "GAMMA(X)" OUTPUT_STREAM)
(PRINT (GAMMA X) OUTPUT_STREAM)
(PRINT '--------------------- OUTPUT_STREAM)
)
;ОТКРЫВАЕМ ФАЙЛ ДЛЯ ЧТЕНИЯ
(SETQ INPUT_STREAM (OPEN " D:\\INPUT_DATA.TXT" :DIRECTION :INPUT))
;ПОЛУЧАЕМ ПАРАМЕТР ФУНКЦИИ
(SETQ X (READ INPUT_STREAM))
;ЗАКРЫВАЕМ ФАЙЛ
(CLOSE INPUT_STREAM)
;ОТКРЫВАЕМ ФАЙЛ ДЛЯ ЗАПИСИ
(SETQ OUTPUT_STREAM (OPEN "D:\\RESULT.TXT" :DIRECTION :OUTPUT))
;ПЕЧАТАЕМ РЕЗУЛЬТАТ ВЫЧИСЛЕНИЯ НЕЭЕЛЕМЕНТАРНЫХ ФУНКЦИЙ
(MAPCAR 'PRINT_RESULT X)
;ЗАКРЫВАЕМ ФАЙЛ
(TERPRI OUTPUT_STREAM)
(CLOSE OUTPUT_STREAM)
;КОНЕЦ
5 Пример выполнения программы
Пример 1.

Рисунок 10 – Входные данные. Параметры функций

Рисунок 11 – Выходные данные. Вычисление неэлементарных функций
Пример 2.
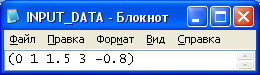
Рисунок 12 – Входные данные. Параметры функций

Рисунок 13 – Выходные данные. Вычисление неэлементарных функций
ЗАКЛЮЧЕНИЕ
Проблема повышения качества вычислений, как несоответствие между желаемым и действительным, существует и будет существовать в дальнейшем. Ее решению будет содействовать развитие информационных технологий, которое заключается как в совершенствовании методов организации информационных процессов, так и их реализации с помощью конкретных инструментов – сред и языков программирования.
Итогом работы можно считать созданную функциональную модель вычисления неэлементарных функций. Данная модель применима к функциям, если она не задана одной формулой посредством конечного числа операций: сложения, вычитания, умножения, деления и взятия функции от функции - над основными элементарными функциями.
Созданная функциональная модель реализации основных способов вычисления гамма функции и ее программная реализация могут служить органической частью решения более сложных задач.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ и литературы
1. Бронштейн, И.Н. Справочник по математике для инженеров и учащихся втузов [Текст] / И.Н. Бронштейн, К.А. Семендяев. – М.: Наука, 2007. – 708 с.
2. Вычисление гамма-функции и бета-функции [Электронный ресурс] – Режим доступа: http://www.cyberguru.ru/cpp-sources/algorithms/vytchislenie-gamma-funktsii-i-beta-funktsii.html
3. Гамма-функция – Википедия [Электронный ресурс] – Режим доступа: http://ru.wikipedia.org/wiki/Гамма_функция
4. Кремер, Н.Ш. Высшая математика для экономистов: учебник для студентов вузов. [Текст] / Н.Ш.Кремер, 3-е издание – М.:ЮНИТИ-ДАНА, 2006. C. 412.
5. Семакин, И.Г. Основы программирования. [Текст] / И.Г.Семакин, А.П.Шестаков. – М.: Мир, 2006. C. 346.
6. Симанков, В.С. Основы функционального программирования [Текст] / В.С. Симанков, Т.Т. Зангиев, И.В. Зайцев. – Краснодар: КубГТУ, 2002. – 160 с.
7. Степанов, П.А. Функциональное программирование на языке Lisp. [Электронный ресурс] / П.А.Степанов, А.В. Бржезовский. – М.: ГУАП, 2003. С. 79.
8. Хювенен Э. Мир Лиспа [Текст] / Э. Хювенен, Й. Сеппянен. – М.: Мир, 1990. – 460 с.
Похожие работы
... . В частности: (8) Из (7) и (8) следует, что в M нет двух неравных натуральных чисел. Доказательство закончено. 3.2 Рекурсия Особое место для систем функционального программирования приобретает рекурсия, поскольку она позволяет учитывать значения функции на предыдущих шагах. С теоретической точки зрения рекурсивные определения являются теоретической основой всей современной ...
... По теореме 9.3 в силу результатов шагов 3 и 8. (Шаг 10). Имеет место свойство (9.4) по теореме 9.5 в силу результатов шагов 1 и 9. Литература к лекции 9. 9.1. С.А. Абрамов. Элементы программирования. - М.: Наука, 1982. С. 85-94. 9.2. М. Зелковец, А. Шоу, Дж. Гэннон. Принципы разработки программного обеспечения. - М.: Мир, 1982. С. 98-105. Лекция 10. ТЕСТИРОВАНИЕ И ОТЛАДКА ПРОГРАММНОГО ...
... проектирование и программирование 0.8 Структурное проектирование включает в себя: - нисходящее проектирование ("сверху вниз"), - модульное программирование, - структурное программирование. 0.8.1.Нисходящее проектирование Метод предполагает последовательное разложение функции обработки данных на простые функциональные элементы ("сверху ...
... . Объясните, для чего служат разрешения и привилегии в Windows NT. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету СИСТЕМНОЕ ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ Билет № 22 Перечислите возможности и инструменты системы программирования Microsoft Developer Studio. Укажите для чего предназначается буфер в системах ввода-вывода, ...

0 комментариев