Навигация
Численные методы решения систем линейных уравнений
Курсовая работа
по информатике на тему:
«Численные методы решения
систем линейных уравнений»
Выполнил:
студент 06–ИСТ, Фадеева Т.В.
Проверил:
Ловыгина М.Б.
г. Павлово
2008
Содержание.
I Теоретическая часть
1. Введение....................................................................3
2. Численные методы ..................................................6
1) Матричный метод........................................6
2) Метод Крамера.............................................9
3) Метод Гаусса …………...............................12
4) Итерации для линейных систем….…..…..17
a) Итерация Якоби..………………...…..18
b) Итерация Гаусса – Зейделя..……...…20
II Практическая часть
1) Матричный метод........................................22
2) Метод Крамера.............................................24
3) Метод Гаусса……........................................26
4) Листинг программы.……………………….28
III Польза введения расчётов.……………………………….65
IV Литература……….................................................................66
I. Теоретическая часть.
Введение.
Линейная алгебра – часть алгебры, изучающая векторные (линейные) пространства и их подпространства, линейные отображения (операторы), линейные, билинейные, и квадратичные функции на векторных пространствах.
Линейная алгебра, численные методы – раздел вычислительной математики, посвященный математическому описанию и исследованию процессов численного решения задач линейной алгебры.
Среди задач линейной алгебры наибольшее значение имеют две: решение системы линейных алгебраических уравнений определение собственных значений и собственных векторов матрицы. Другие часто встречающиеся задачи: обращение матрицы, вычисление определителя и т.д.
Любой численный метод линейной алгебры можно рассматривать как некоторую последовательность выполнения арифметических операций над элементами входных данных. Если при любых входных данных численный метод позволяет найти решение задачи за конечное число арифметических операций, то такой метод называется прямым. В противоположном случае численный метод называется итерационным. Прямые методы - это такие, как метод Гаусса, метод окаймления, метод пополнения, метод сопряжённых градиентов и др. Итерационные методы – это метод простой итерации, метод вращений, метод переменных направлений, метод релаксации и др. Здесь будут рассматриваться матричный метод, метод Гаусса и метод Крамера.
В данной работе будут рассмотрены численные методы в электронных таблицах Excel и программе MathCAD, Microsoft Visual Basic.
MathCAD.
Программа MathCAD по своему назначению позволяет моделировать в электронном документе научно–технические, а также экономические расчёты в форме, достаточно близкой к общепринятым ручным расчётам. Это упрощает составление программы расчёта, автоматизирует перерасчёт и построение графических иллюстраций подобно электронным таблицам Excel, документирование результатов как в текстовом редакторе Word.
Программа Mathcad известна за лёгкость, с которой математические уравнения, текст, и графика могут быть объединены в одном документе. Кроме того, вычислительные способности Mathcad распространяются от сложения столбца чисел к решению интегралов и производных, решение систем уравнений и больше.
Достоинством MathCAD является также наличие в его составе электронных книг. Одна из них – учебник по самой программе, другие – справочник по различным разделам математики, физики, радиоэлектроники и др.
Microsoft Office Excel.
Если же говорить о программе Excel, которая является одной из наиболее известных в обработке электронных таблиц, то без преувеличения можно утверждать, что ее возможности практически неисчерпаемы.
Обработка текста, управление базами данных - программа настолько мощна, что во многих случаях превосходит специализированные программы - редакторы или программы баз данных. Такое многообразие функций может поначалу запутать, нежели заставить применять их на практике. Но по мере приобретения опыта начинаешь по достоинству ценить то, что границ возможностей Excel тяжело достичь.
За всю историю табличных расчетов с применением персональных компьютеров требования пользователей к подобным программам существенно изменились. В начале основной акцент в такой программе, как, например, Visi Calc, ставился на счетные функции. Сегодня, положение другое. Наряду с инженерными и бухгалтерскими расчетами организация и графическое изображение данных приобретают все возрастающее значение. Кроме того, многообразие функций, предлагаемое такой расчетной и графической программой, не должно осложнять работу пользователя. Программы для Windows создают для этого идеальные предпосылки.
В последнее время многие как раз перешли на использование Windows в качестве своей пользовательской среды. Как следствие, многие фирмы, создающие программное обеспечение, начали предлагать большое количество программ для Windows.
Visual Basic.
Microsoft Visual Basic – это мощная система программирования, позволяющая быстро и эффективно создавать приложения для Microsoft Windows. В отличие от Excel и MathCAD это наиболее удобная программа для решения систем линейных уравнений. Простой пользовательский интерфейс, позволяющий легко переключаться с проекта формы на сам код программы.
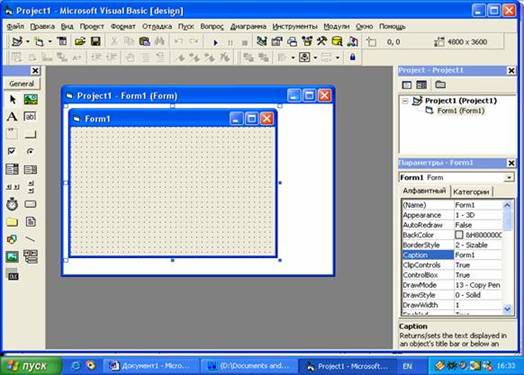
Удобное окно для кода самой программы:
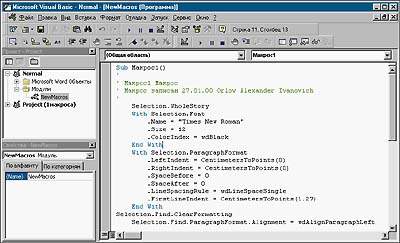
Численные методы.
Разрешимость системы линейных уравнений.
Когда мы говорим о главной матрице системы линейных уравнений, то всегда имеем в виду квадратную матрицу n×n, т. е. матрицу с одинаковым количеством строк и столбцов. Это важно.
Если, например, количество строк (количество уравнений в системе) будет меньше, чем количество столбцов (фактически, количества неизвестных), то система будет неопределенной, т. е. мы не сможем однозначно определить все неизвестные (решить систему).
Но это не единственное ограничение. Из векторной алгебры известно, что система линейных уравнений имеет решение (однозначное) тогда и только тогда, когда ее главный определитель не равен нулю: Δ ≠ 0.
Рассмотрим случай, когда определитель системы равен нулю. Здесь возможны два варианта:
1. Δ = 0 и каждый из дополнительных определителей Δxi = 0. Это имеет место только тогда, когда коэффициенты при неизвестных xi пропорциональны, т. е. каждое уравнение системы получается из первого уравнения умножением обеих его частей на число k. При этом система имеет бесчисленное множество решений.
2. Δ = 0 и хотя бы один дополнительный определитель Δxi ≠ 0. Это имеет место только тогда, когда коэффициенты при всех неизвестных xi, пропорциональны. При этом получается система из противоречивых уравнений, которая не имеет решений.
Матричный метод решения систем линейных уравнений.
Пусть дана система линейных уравнений:
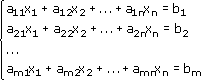
Рассмотрим матрицу, составленную из коэффициентов при неизвестных:
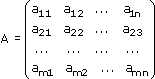
Свободные члены и неизвестные можно записать в виде матрицы столбцов:
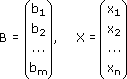
Тогда, используя правило умножение матриц, эту систему уравнений можно записать так:
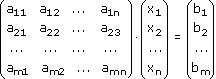
или
A·x = b. (1)
Равенство (1) называется матричным уравнением или системой уравнений в матричном виде.
Матрица А коэффициентов при неизвестных называется главной матрицей системы.
Иногда рассматривают также расширенную матрицу системы, т. е. главную матрицу системы, дополненную столбцом свободных членов, которую записывают в следующем виде:
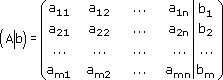
Любую линейную систему уравнений можно записать в матричном виде. Например, пусть дана система:
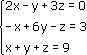
Эта система из двух уравнений с тремя неизвестными – x, y,. В высшей математике можно рассматривать системы из очень большого числа уравнений с большим количеством неизвестных и поэтому неизвестные принято обозначать только буквой х, но с индексами:
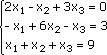
Запишем эту систему в матричном виде:
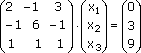
Здесь главная матрица системы:
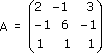
Расширенная матрица будет иметь вид:
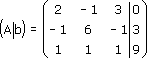
Решения матричных уравнений.
Матричные уравнения решаются при помощи обратных матриц. Уравнение решается следующим образом. Пусть матрица А – невырожденная (D ≠ 0), тогда существует обратная матрица А-1. Умножив на нее обе части матричного уравнения, имеем А-1(АХ) = А-1В. Используя сочетательный закон умножения, перепишем это равенство в виде
(А-1А) Х = А-1В.
Поскольку А-1 А = Е и ЕХ = Х, находим:
Х = А-1В.
Таким образом, чтобы решить матричное уравнение, нужно:
1. Найти обратную матрицу А-1.
2. Найти произведение обратной матрицы А-1 на матрицу столбец свободных членов В, т. е А-1В.
Пользуясь определением равных матриц, записать ответ.
При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений.
К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над расширенной матрицей системы. А в методе Крамера – с определителями системы, образованными по специальному правилу.
Метод Крамера.
При решении систем линейных уравнений по методу Крамера последовательно выполняется следующий алгоритм:
1. Записывают систему в матричном виде (если это еще не сделано).
2. Вычисляют главный определитель системы:
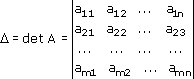
3. Вычисляют все дополнительные определители системы:

4. Если главный определитель системы не равен нулю, то выполняют пункт 5. Иначе рассматривают вопрос о разрешимости данной системы (имеет бесчисленное множество решений или не имеет решений). Находят значения всех неизвестных по формулам Крамера для решения системы n линейных уравнений с n неизвестными, которые имеют вид:
![]()
Пример 1
Решить по методу Крамера систему из трех уравнений с тремя неизвестными:
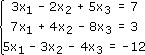
Решение
Запишем главный и побочные определители системы:
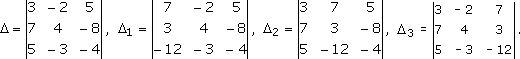
Вычислим эти определители:
Δ = 3*4*(-4)+7*(-3)*5+(-2)*(-8)*5-5*4*5-3*(-3)*(-8)-7*(-2)*(-4) = 48-105+80-100-72-56 = 128-333 = -205.
Δ1 = -112+(-45)+(-192)-(-240)-24-168 = -112-45-192+240-24-168 = 240-541 = -301.
Δ2 = -36-420-280-75+196-288 = 196-1099 = -903.
Δ3 = -144-147-30-140+27-168 = -629+27 = -602.
Главный определитель системы не равен нулю. Находим неизвестные по формулам Крамера.
Подставим найденные значения определителей в формулы Крамера:
x1 = Δ1/Δ = -301/(-205) = 1,468292682927 ≈ 1,47;
x2 = Δ2/Δ = -903/(-205) = 4,40487804878 ≈ 4,4;
x3 = Δ3/Δ = -602/(-205) = 2,936585365854 ≈ 2,93.
Вывод.
При решении систем линейных уравнений по методу Крамера используются формулы, в которых участвуют как главный, так и дополнительные определители системы:
![]()
Напомним, что главным определителем системы называется определитель главной матрицы системы, составленной из коэффициентов при неизвестных:

Если в главном определителе системы заменить поочередно столбцы коэффициентов при x1, x2,...xn на столбец свободных членов, то получим n дополнительных определителей (для каждого из n неизвестных):

При этом важен вопрос о разрешимости данной системы, который решается сравнением главного и дополнительных определителей системы с нулем:

Метод Гаусса – прямой и обратный ход.
Рассмотрим метод Гаусса. Например, пусть дана расширенная матрица некоторой системы m линейных уравнений c n неизвестными:

Будем считать, что a11 ≠ 0 (если это не так, то достаточно переставить первую и некоторую другую строку расширенной матрицы местами). Проведем следующие элементарные преобразования:
C2-(a21/a11)*C1,
...
Cm-(am1/a11)*C1,
т.е. Ci-(ai1/a11)*C1, i = 2, 3, ..., m.
Т. е. от каждой строки расширенной матрицы (кроме первой) отнимаем первую строку, умноженную на частное от деления первого элемента этой строки на диагональный элемент а11.
В результате получим матрицу:

Т. е. первая строка осталась без изменений, а в столбце под а11 на всех местах оказались нули. Обратим внимание, что преобразования коснулись всех элементов строк, начиная со второй, всей расширенной матрицы системы.
Теперь наша задача состоит в том, чтобы получить нули подо всеми диагональными элементами матрицы А – aij, где I = j.
Повторим наши элементарные преобразования, но уже для элемента α22.
C1-(a12/α22)*C2,
...
Cm-(αm2/α22)*C2,
т.е. Ci-(αi2/α22)*C2, i = 3, ..., m.
Т. е. от каждой строки расширенной матрицы (теперь кроме первой и второй) отнимаем вторую строку, умноженную на частное от деления первого элемента этой (текущей) строки на диагональный элемент α22.
Такие преобразования продолжаются до тех пор, пока матрица не приведется к верхнее - треугольному виду. Т. е. под главной диагональю не окажутся все нули:

Вспомнив, что каждая строка представляет собой одно из уравнений линейной системы уравнений, легко заметить, что последнее m-ое уравнение принимает вид:
γmn*xn = δm.
Отсюда легко можно найти значение первого корня – xn = δm/γmn.
Подставив это значение в предыдущее m-1-е уравнение, легко получим значение xn-1-ого корня.
Таким образом, поднимаясь до самого верха обратным ходом метода Гаусса, мы последовательно найдем все корни системы уравнений.
Пример 1
Рассмотрим систему уравнений:
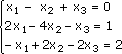
Главный определитель данной системы:
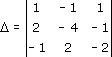
Δ = [1*(-4)*(-2)+2*2*1+(-1)*(-1)*(-1)]-[1*(-4)*(-1)+2*(-1)*(-2)+2*(-1)*1] = [8+4-1]-[4+4-2] = 11-6 =5,
т. е. Δ ≠ 0.
Т. е. система определена и разрешима. Решим ее по методу Гаусса.
Проведем прямой ход метода Гаусса, выписав предварительно расширенную матрицу системы:
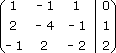
Получим нули под главной диагональю в первом столбце расширенной матрицы. Для получения нуля в элементе a21 (т. е. под диагональю во второй строке матрицы) вторую строку матрицы преобразуем по формуле C2-(a21/a11)*C1 = C2-(2/1)*C1 = C2-2*C1:
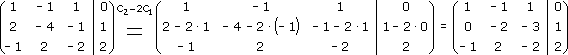
Аналогично поступаем и с элементом а31 (т. е. под диагональю в третьей строке матрицы). Третью строку матрицы преобразуем по формуле C3-(a31/a11)*C1 = C3-(-1/1)*C1 = C3+C1:
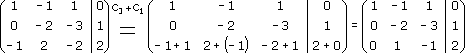
Таким образом, мы получили нули под главной диагональю в первом столбце расширенной матрицы. Осталось получить нуль под главной диагональю во втором столбце матрицы, т. е. на месте элемента а32. Для этого третью строку матрицы преобразуем по формуле C3-(a32/a22)*C2 = C3-(1/-2)*C2 = C3+1/2C2:
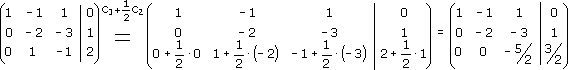
Таким образом, проведя прямой ход метода Гаусса, мы получили расширенную матрицу системы, приведенную к верхне-треугольному виду:
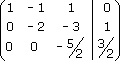
Эта матрица эквивалентна системе:
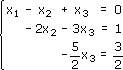
Обратным ходом метода Гаусса найдем корни системы. Из последнего уравнения найдем корень х3:
-5/2x3 = 3/2,
x3 = (3/2):(-5/2) = 3/2*(-2/5) = -3/5.
Корень x3 = -3/5 найден. Подставим его в верхнее (второе) уравнение системы (-2x2-3x3 = 1):
-2x2-3(-3/5) = 1,
-2x2+9/5 = 1,
-2x2 = 1-9/5,
-2x2 = -4/5,
x2 = (-4/5):(-2) = (-4/5)*(-1/2) = 2/5.
Корень x2 = 2/5 найден. Подставим его и корень х3 в верхнее (первое) уравнение системы (x1-x2+x3 = 0):
x1-2/5+(-3/5) = 0,
x1-5/5 = 0,
x1 = 5/5 = 1.
Проверка:
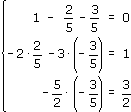
т. е.
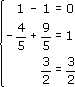
т. е.
![]()
и т. д.
Вывод.
Итак, метод Гаусса (или, иначе, метод последовательного исключения неизвестных) состоит в следующем:
1. Путем элементарных преобразований систему уравнений приводят к эквивалентной ей системе с верхне-треугольной матрицей. Эти действия называют прямым ходом.
2. Из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход).
3. При этом все преобразования проводятся над так называемой расширенной матрицей системы, которую и приводят к верхнее - треугольному виду в прямом ходе метода.
Итерация для линейных систем.
Способ итераций дает возможность получить последовательность приближенных значений, сходящихся к точному решению системы, подобно тому, как это делается для одного уравнения.
Для определенности ограничимся системой из четырех уравнений с четырьмя неизвестными (система четвертого порядка), которую запишем в виде:
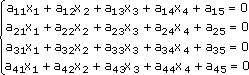
Разрешим первое уравнение системы относительно х1:
х1 = (-a12/a11)х2-a13/a11х3-a14/a11х4-a15/a11.
Затем разрешим второе уравнение относительно х2 и т. д. Тогда систему можно переписать в виде:
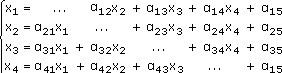
где α = -aik/aii, i = 1, 2, 3, 4; k = 1, 2, 3, 4, 5.
Система является частным случаем записи вида:
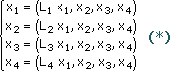
При этом линейная функция L1 фактически не зависит от х1.
Зададим какие-либо начальные значения неизвестных (нулевые приближения):
х1(0), х2(0), х3(0), х4(0).
Подставляя эти значения в правые части системы (*), получим первые приближения:
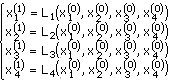
Полученные первые приближения могут быть так же использованы для получения вторых, третьих и т. д. приближений. Т. е. можно записать:
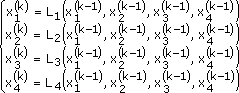
Условия сходимости итерационного процесса.
Установим условия, выполнение которых обеспечит сходимость получающихся приближений к истинному (точному) решению системы х1, х2, х3, х4.
Не вдаваясь в подробности, скажем, что для того чтобы итерационный процесс сходился к точному решению, достаточно, чтобы все коэффициенты системы были малы по сравнению с диагональными.
Это условие можно сформулировать и более точно:
Для сходимости процесса итераций достаточно, чтобы в каждом столбце сумма отношений коэффициентов системы к диагональным элементам, взятым из той же строки, была строго меньше единицы:
![]()
Итерация Якоби.
Рассмотрим систему линейных уравнений:
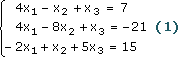
Уравнения можно записать в виде:
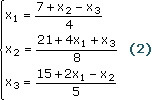
Это позволяет предложить следующий итерационный процесс:
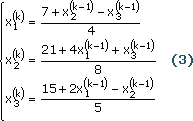
или (другой вид записи)
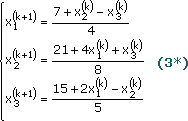
Покажем, что если начать с точки P0 = (х1(0), х2(0), х3(0), х4(0)) = (1, 2, 2), то итерация (3) сходится к решению (2, 4, 3). Подставим х1 = 1, х2 = 2, х2 = 2 в правую часть каждого уравнения из (3), чтобы получить новые значения:
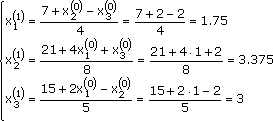
Новая точка P1 = (х1(1), х2(1), х3(1), х4(1)) = (1.75, 3.375, 3), ближе, чем P0.
Итерация, использующая (3), генерирует последовательность точек {Pk}, которая сходится к решению (2, 4, 3):
| k | х1(k) | х2(k) | х3(k) |
| 0 | 1.0 | 2.0 | 2.0 |
| 1 | 1.75 | 3.375 | 3.0 |
| 2 | 1.84375 | 3.875 | 3.025 |
| 3 | 1.9625 | 3.925 | 2.9625 |
| 4 | 1.990625 | 3.9765625 | 3.0 |
| 5 | 1.99414063 | 3.9953125 | 3.0009375 |
| … | … | … | … |
| 15 | 1.99999993 | 3.99999985 | 3.0009375 |
| … | … | … | … |
| 19 | 2.0 | 4.0 | 3.0 |
Этот процесс называется итерацией Якоби и может использоваться для решения определенных типов линейных систем.
Итерация Гаусса-Зейделя.
Процесс итерации Якоби иногда можно модифицировать для ускорения сходимости.
Отметим, что итеративный процесс Якоби производит три последовательности – {х1(k)}, {х2(k)}, {х3(k)}, {х4(k)}. Кажется разумным, что х1(k+1) может быть использовано вместо х2(k). Аналогично х1(k+1) и х2(k+1) можно использовать в вычислении х3(k+1). Например, для уравнений из системы (1) это даст следующий вид итерационного процесса Гаусса-Зейделя, использующий (3*):
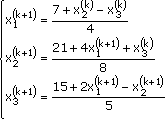
Такой итерационный процесс даст результаты:
| k | х1(k) | х2(k) | х3(k) |
| 0 | 1.0 | 2.0 | 2.0 |
| 1 | 1.75 | 3.75 | 2.95 |
| 2 | 1.95 | 3.96875 | 2.98625 |
| 3 | 1.995625 | 3.99609375 | 2.99903125 |
| … | … | … | … |
| 8 | 1.99999983 | 3.99999988 | 2.99999996 |
| 9 | 1.99999998 | 3.99999999 | 3.0 |
| 10 | 2.0 | 4.0 | 3.0 |
Т. е. к точному решению мы пришли уже на 10-ом шаге итерации, а не на 19, как в итерации Якоби.
Вывод.
1. Способ итераций дает возможность получить последовательность приближенных значений, сходящихся к точному решению системы. Для этого система приводится к виду (для случая системы из четырех уравнений):
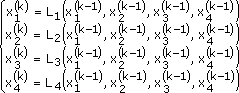
Эти формулы как раз и задают собственно итерационный процесс.
Похожие работы
... , с помощью которых в последующем решение систем линейных уравнений станет намного проще, понятнее и быстрее. Цель моей работы заключается в том, чтобы изучить различные способы решения систем линейных уравнений для применения их на практике. Для достижения любой цели необходимо выполнить какие-то определенные задачи. Мне нужно выполнить следующие задачи: исследовать литературу по темам матриц, ...
... - функции f. Дальше, имеем: . Отсюда , где W'(x) - транспонированная матрица Якоби. Поэтому окончательно , причем . 3. Программная реализация итерационных методов Реализация алгоритмов итерационных методов решения систем нелинейных уравнений будет показана на примере системы: 3.1 Метод простых итераций Приведём систему к виду: Проверим условие ...
... треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода. Целью данной курсовой работы является численное решение системы линейных уравнений с помощью метода исключения Гаусса с выбором главного элемента по столбцу. 1 Постановка задачи Задача ставится следующим образом. Пусть требуется найти решение системы линейных алгебраических уравнений a1,1x1 + a1, ...
... -1 х3 = 1 х4 = 2 3. Преимущества и недостатки метода Гаусса Итак, метод Гаусса применим к любой системе линейных уравнений, он идеально подходит для решения систем, содержащих больше трех линейных уравнений. Метод Гаусса решения СЛАУ с числовыми коэффициентами в силу простоты и однотипности выполняемых операций пригоден для счета на электронно-вычислительных машинах. Достоинства метода: ...
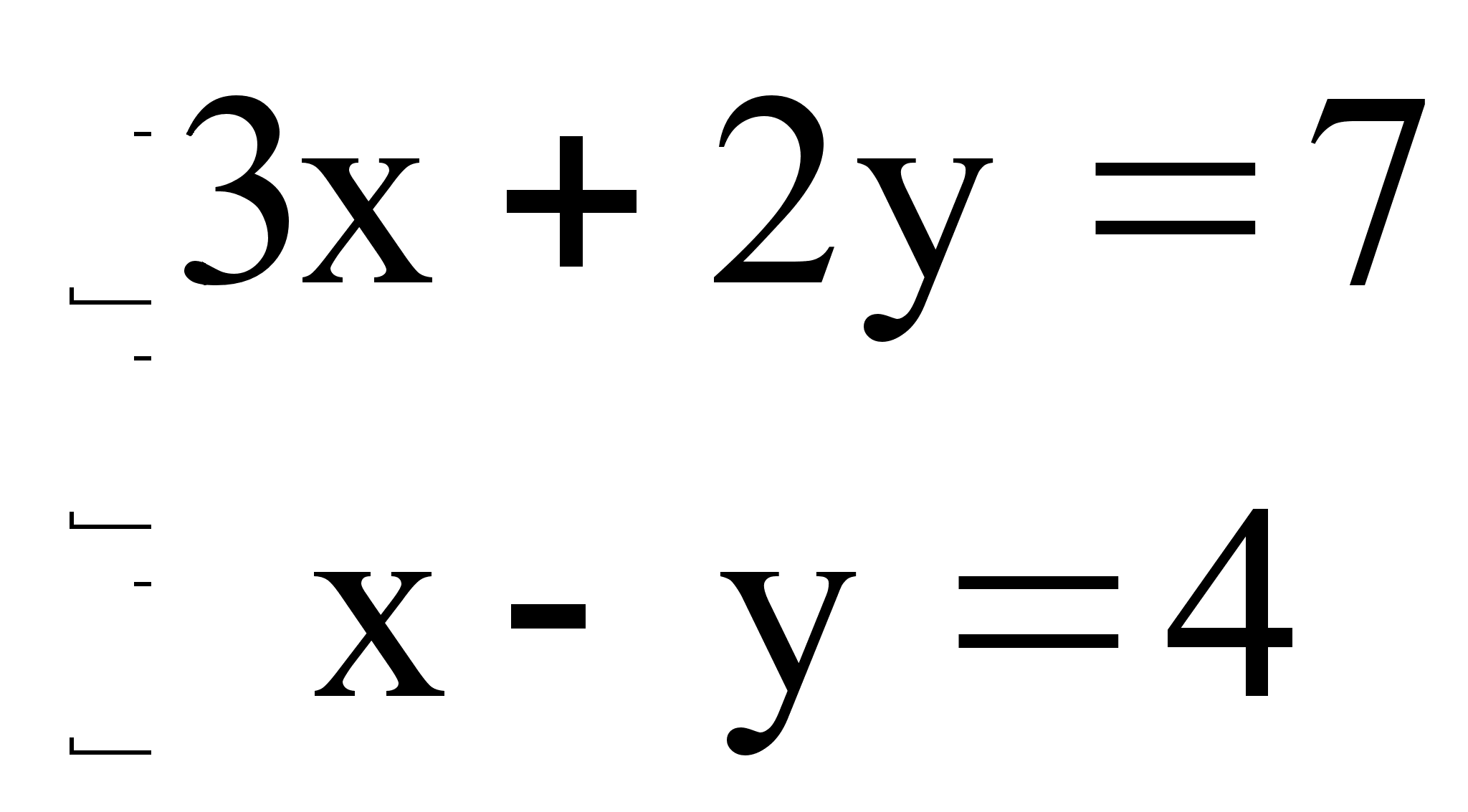
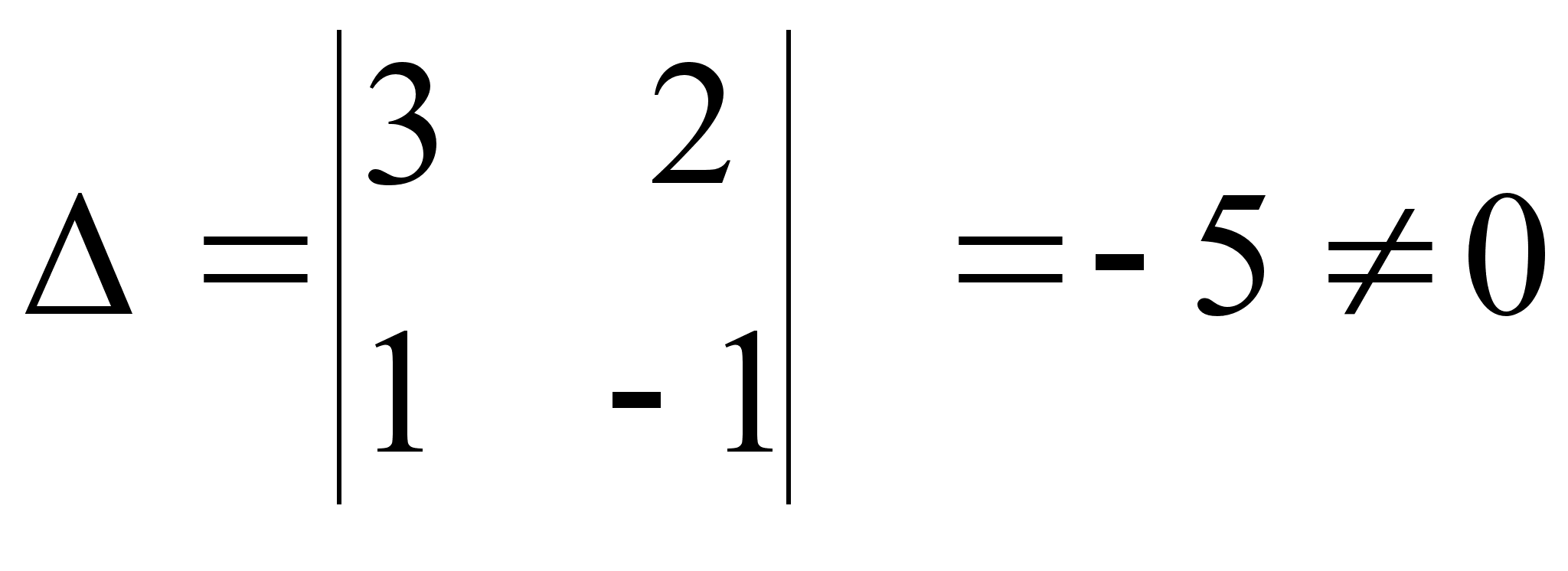
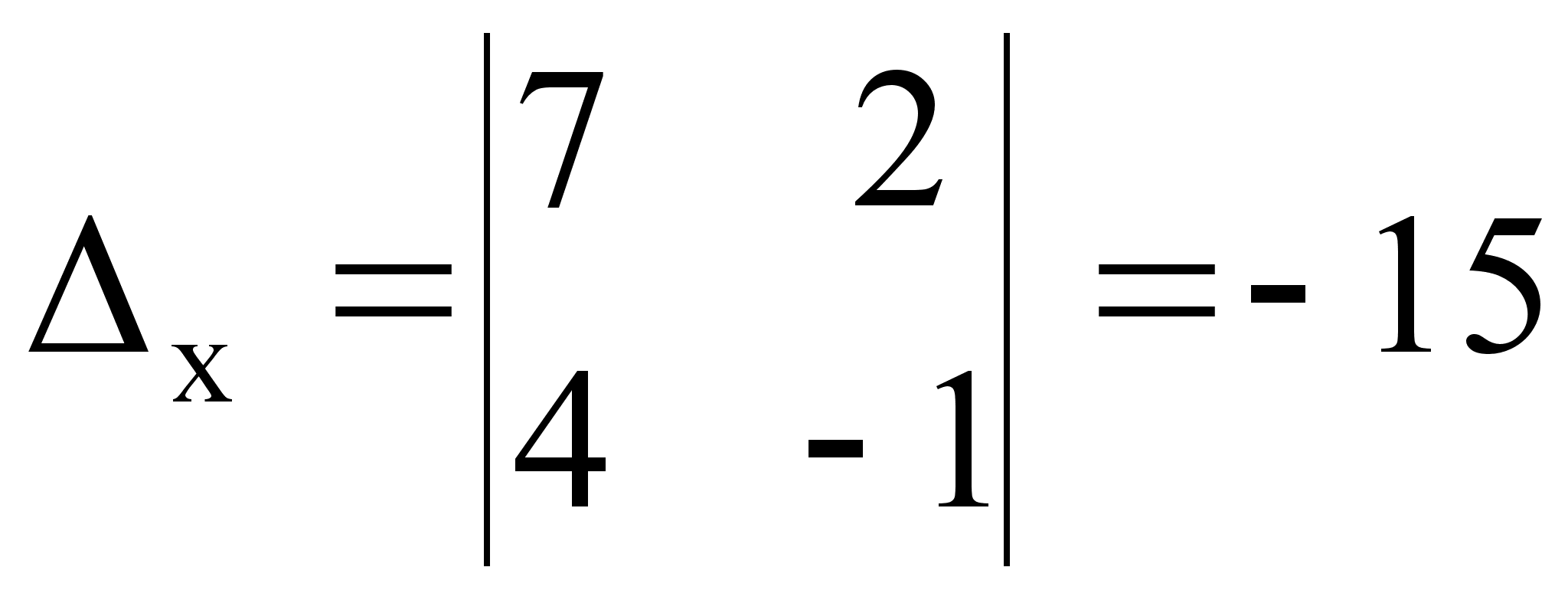
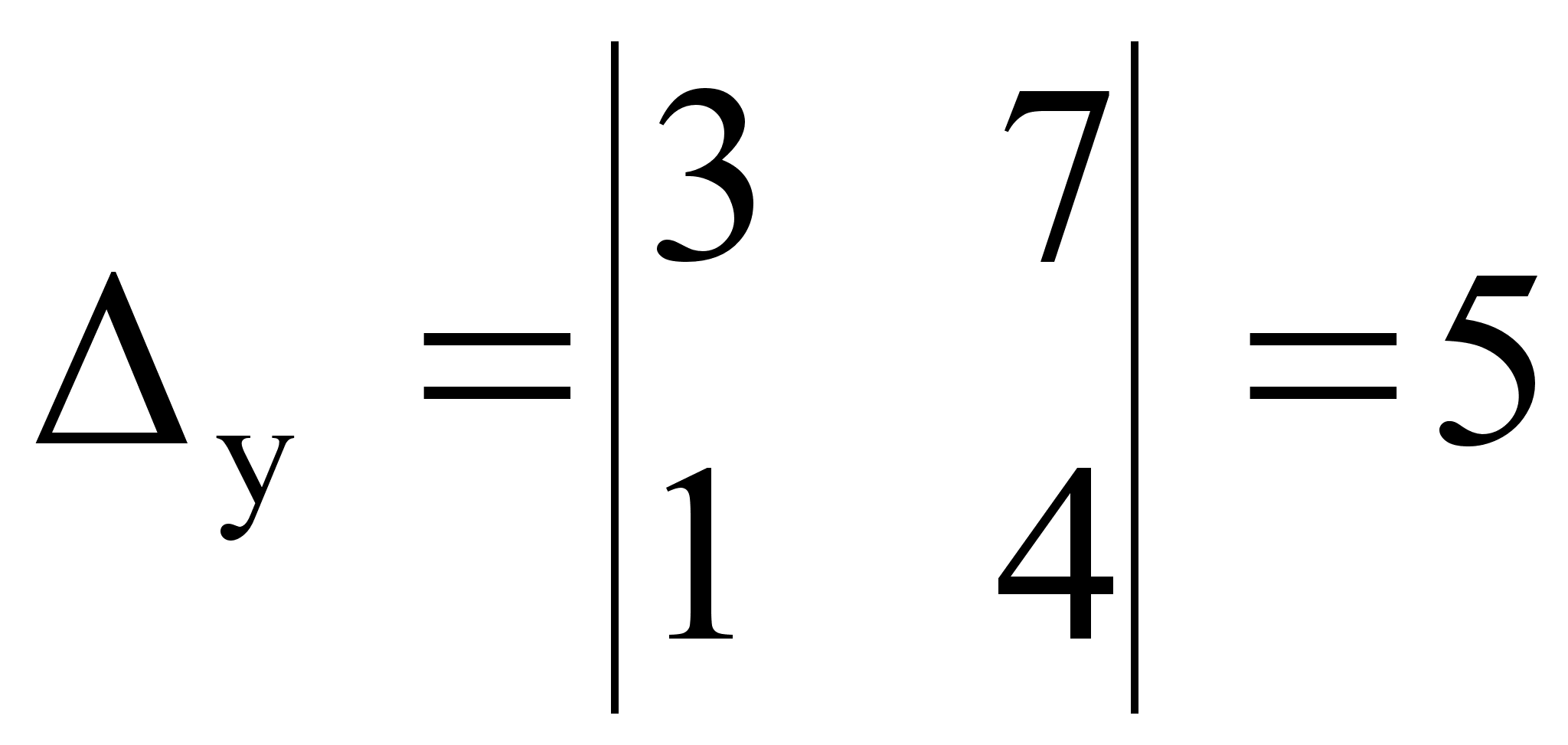
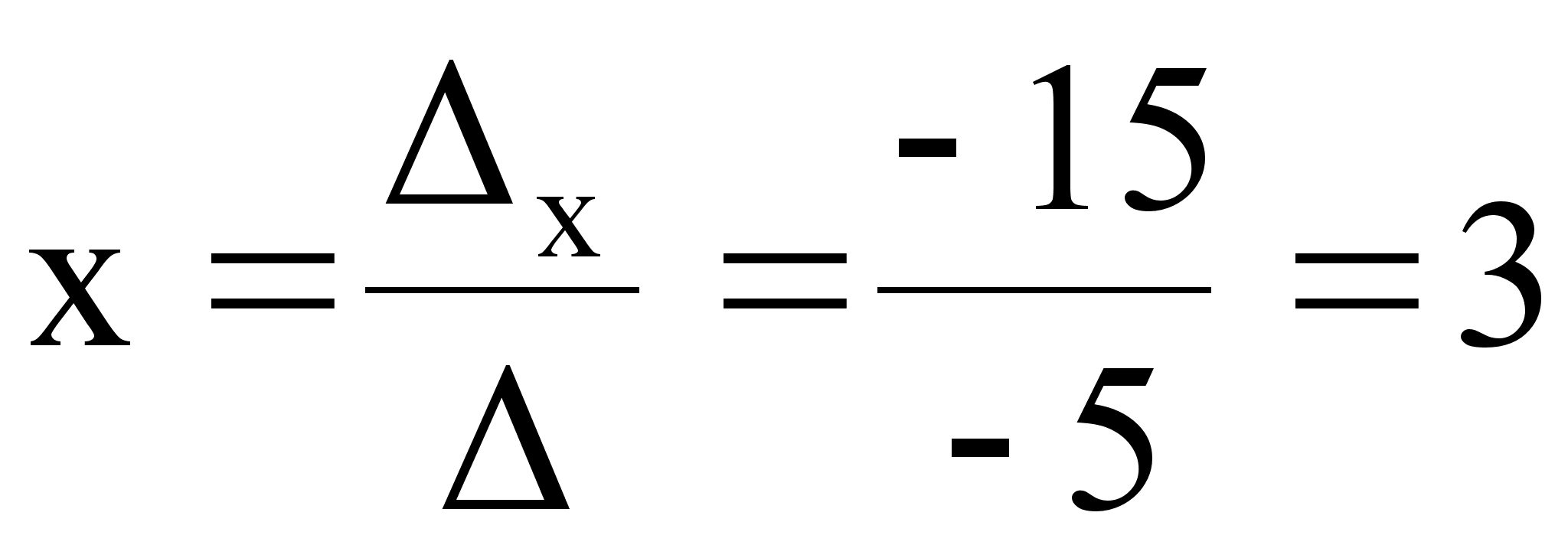


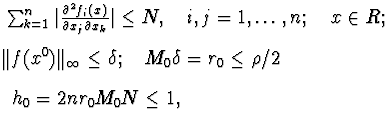
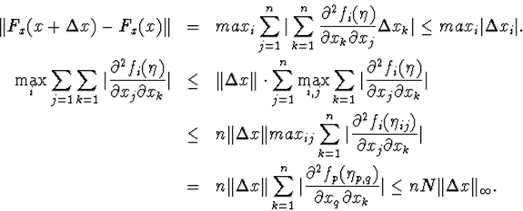
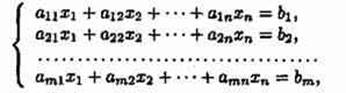
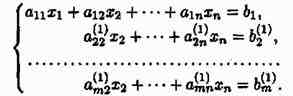

0 комментариев