Министерство образования Республики Беларусь
Белорусский государственный университет информатики и радиоэлектроники
Кафедра Электронных вычислительных средств
Отчет по лабораторной работе
"Дискретное преобразование Фурье"
Выполнила:
Студентка гр. 610701
Лыпка Ю.А.
Проверил: Родионов М. М.
Минск 2009
1. Цель работы
Программирование дискретного преобразования Фурье в пакете Matlab. Изучение свойств ДПФ.
2 Выполнение заданий.
Задание 1-2
Разработайте функцию DFT, вычисляющую ДПФ от входного вектора, не используя функцию Matlab FFT, и рисующую графики действительной и мнимой частей входного вектора и результата преобразования, а также амплитудный спектр.
clear all;
close all;
clc;
n = 0:99;
k=(2*pi/length(n)).*n
s = (n >= 0) & (n <= 9);
figure(1);
subplot(221);
stem(n, real(s),'x');
title('Re(s(n))');
subplot(222);
stem(n, imag((s)),'x');
title('Im(s(n))');
subplot(223);
stem(k, abs(dft(s)),'x');
xlabel('\omega');
title('|S(k)|');
subplot(224);
stem(k, abs(dft(s)),'x');
title('|S(k)| cherez fft');
xlabel('\omega');
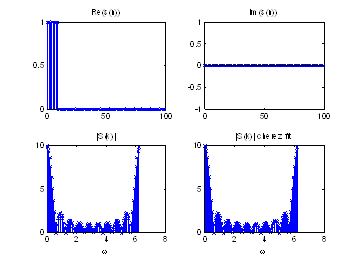
Рисунок 1 – Реальная и мнимая часть входного вектора, амплитудный спектр.
Задание 3
Исследуйте свойства симметрии ДПФ при следующих входных сигналах: действительном; мнимом; действительном четном; мнимом четном; действительном нечетном; действительном симметричном четном. Длину входного вектора выберите в соответствии с вариантом 2: N=35.
clear all;
%% 3 zadanie
N = 35;
n = 0:2*pi/N:2*pi;
figure;
subplot(311);
x = sin(n) + cos(n); % действительный входной сигнал
plot(n,x,'x');
title('real signal');
xlabel('n');
ylabel('Re(x)');
subplot(312);
plot(n, real(fft(x)));
title('real part of real signal');
xlabel('n');
ylabel('Re(x)');
subplot(313);
plot(n, imag(fft(x)));
title('image part of real signal')
xlabel('n');
ylabel('Im(x)');
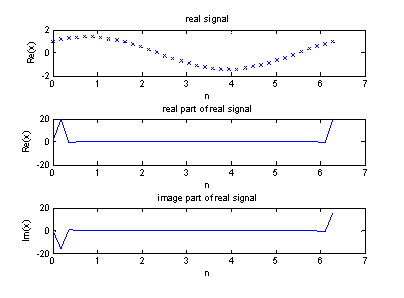
Рисунок 2 – Real, image часть действительного входного сигнала
figure;
subplot(311);
x = j*(sin(n) + cos(n)); % мнимый входной сигнал
plot(n,imag(x),'x');
title('image signal')
xlabel('n');
ylabel('Im(x)');
subplot(312);
plot(n, real(fft(x)));
title('real part of image signal');
xlabel('n');
ylabel('re of Im(x)');
subplot(313);
plot(n, imag(fft(x)));
title('image part of image signal');
xlabel('n');
ylabel('Im of Im(x)');
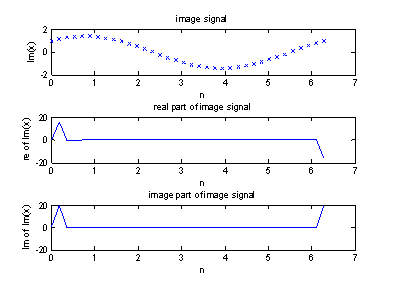
Рисунок 3 – Real, image часть мнимого входного сигнала
figure;
subplot(311);
x = cos(n); % действительный чётный сигнал
plot(n,x,'x');
title('real even signal');
xlabel('n');
ylabel('Re(s)');
subplot(312);
plot(n, real(fft(x)));
title('real part of real even signal');
xlabel('n');
ylabel('Re of Re(x)');
subplot(313);
plot(n, imag(fft(x)));
title('Image part of real even signal');
xlabel('n');
ylabel('Im of Re(s)');
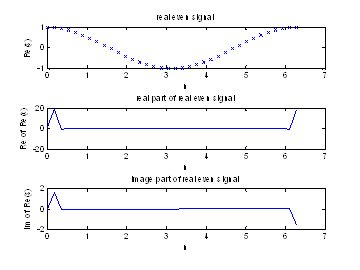
Рисунок 4 – Real, image часть действительного четного входного сигнала
figure;
subplot(311);
x = j*cos(n); % мнимый чётный сигнал
plot(n,imag(x),'x')
title('image even signal');
xlabel('n');
ylabel(' Even Im(x)');
subplot(312);
plot(n, real(fft(x)));
title('real part of image even signal');
xlabel('n');
ylabel('Re of Even Im(x)');
subplot(313);
plot(n, imag(fft(x)));
title('Image part of image even signal');
xlabel('n');
ylabel(' Im of Even Im(x)');
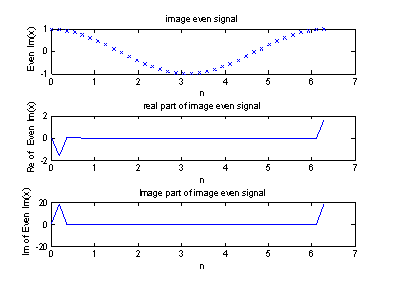
Рисунок 5 – Real, image часть мнимого четного входного сигнала
figure;
subplot(311);
x = sin(n); % действительный нечётный сигнал
plot(n,x,'x');
title('real odd signal')
xlabel('n');
ylabel('Re odd(x)');
subplot(312);
plot(n, real(fft(x)));
title('real part of real odd signal');
xlabel('n');
ylabel('Re of Re(x)');
subplot(313);
plot(n, imag(fft(x)));
title('image part of real odd signal')
xlabel('n');
ylabel('Im of Re(s)');
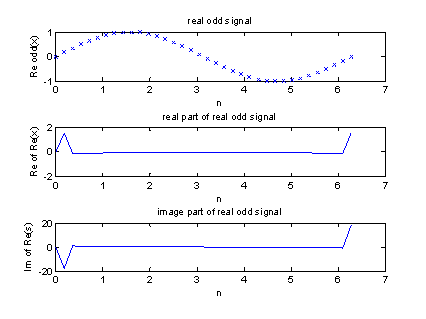
Рисунок 6 – Real, image часть мнимого нечетного входного сигнала
figure;
subplot(311);
n = -N/2:N/2;
x = n.^2; % действительный симметричный сигнал
plot(n,x,'x');
title('real symmetrical signal');
xlabel('n');
ylabel('Re(x)');
subplot(312);
plot(n, real(fft(x)));
title('real part of real symmetrical signal');
xlabel('n');
ylabel('Re of Re(x)');
subplot(313);
plot(n, imag(fft(x)));
title('Image part of real symmetrical signal');
xlabel('n');
ylabel('Im Of Re(x)');
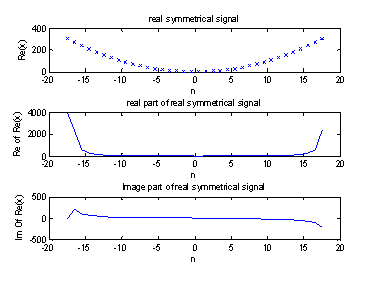
Рисунок 7 – Real, image часть действительного симметричного входного сигнала
Задание 4
Разработайте функцию, позволяющую с помощью ДПФ формировать вектор, содержащий целое число периодов заданной функции. Длину выходного вектора, число периодов и функцию выберите в соответствии с вариантом 2: функция = – cos(x), длинна 90, число периодов 4.
function [x] = cosinus(leng, period);
%генерация функции -cos(x) длиной leng и числом периодов period
X = zeros(1,leng);%инициализируем нулями наш Фурье образ
X(period+1) = (leng-1)/2;%
X(leng-period + 1)= (leng-1)/2;
x = ifft(X);
figure;
Period = 4;
LengV = 90;
stem(cosinus(LengV,Period));
title('Function -cos(x)');
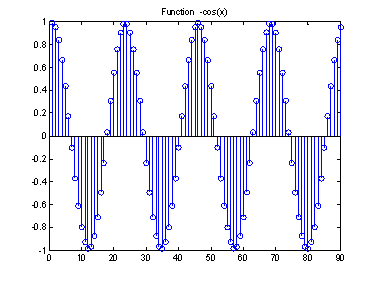
Рисунок 8 – Преобразование Фурье функции –cos(x)
Задание 5
Разработайте функцию, вычисляющую ДПФ для двух действительных векторов одной длины с помощью однократного вызова функции Matlab FFT. Продемонстрируйте ее работу.
%% 5 zadanie
N = 40;
n = 0:N-1;
k=(2*pi/length(n)).*n
x1 = cos(k);
x2 = sin(k);
x = real(x1) + j*real(x2);
y = fft(x);
y(N + 1) = y(1);
for k = 1:N+1
re1(k) = 0.5*(real(y(k)) + real(y(N - k + 2)));
im1(k) = 0.5*(imag(y(k)) - imag(y(N - k + 2)));
re2(k) = 0.5*(imag(y(k)) + imag(y(N - k + 2)));
im2(k) = 0.5*(real(y(N - k + 2)) - real(y(k)));
end;
y1 = re1 + j*im1;
y2 = re2 + j*im2;
subplot(221);
stem(0:N, real(y1));
title('real y1');
subplot(222);
stem(0:N, imag(y1));
title('imag y1');
subplot(223);
stem(0:N, real(y2));
title('real y2');
subplot(224);
stem(0:N, imag(y2));
title('imag y2');
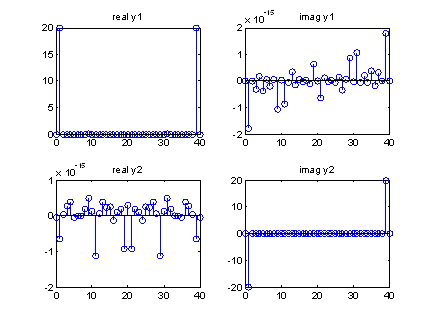
Рисунок 9 – ДПФ для двух действительных векторов х1 и х2
Вывод по работе
При выполнении лабораторной работы мы ознакомились с дискретным преобразованием Фурье, его свойствами и реализацией. В ходе работы были исследованы свойства ДПФ при различных входных сигналах, применено обратное преобразование Фурье при генерации периодической функции косинуса, а также показана возможность вычисления ДПФ двух действительных векторов одинаковой длинны , с помощью однократного вызова функции ДПФ.
Похожие работы
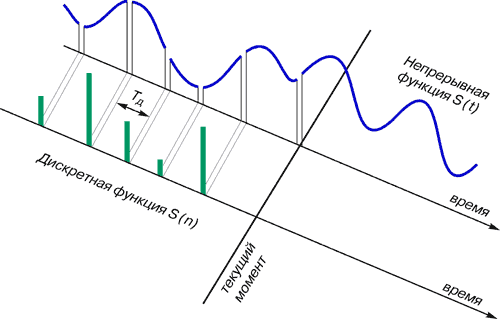
... номерами можно пренебречь ввиду их малости, что не окажет заметного влияния на спектр сигнала. Пример. Осуществить дискретизацию экспоненциального импульса X(t) = Ae-at = 1 e-10t и сравнить спектры исходного и дискретного сигналов. Решение. График сигнала X(t) представлен на Рис. 1.8 Пусть T = 0,02с. В этом случае плавным соединением отсчетов сигнала (штриховая линия на Рис. 1.8) сигнал ...
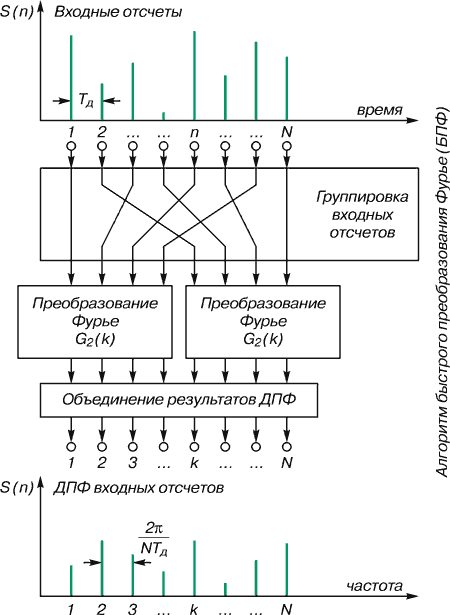
... затрачивается большой объем памяти для хранения промежуточных данных (u,v,p,…). Метод Рунге скорее удобен для вычисления вручную, но менее актуален в программировании. Если говорить о нахождении более оптимального метода расчета коэффициентов Фурье на ЭВМ, то таким является вышеописанное быстрое преобразование Фурье. Он позволяет сократить количество операций до . В сравнении с вышеописанными ...
... условиям представимости интегралом Фурье. Учитывая, что , а также свойство интегралов по симметричному относительно точки x=0 интервалу от четных функций, из равенства (2) получаем: (3) Таким образом, интеграл Фурье четной функции f(x) запишется так: , где a(u) определяется равенством (3). Рассуждая аналогично, получим, для нечетной функции f(x) : (4) и, следовательно, интеграл Фурье ...
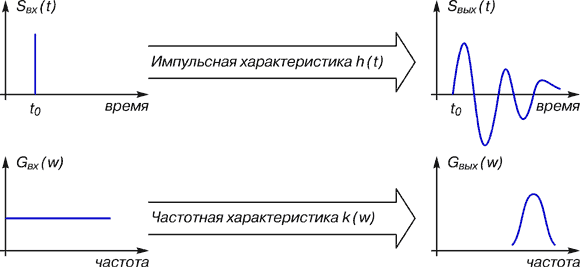
... работы нашего фильтра потребуется представить в частотной области – в виде частотной характеристики K(ω). Δля этого воспользуемся помощью опять-таки «магического стекла» ПФ. Рис. 4. Быстрое преобразование Фурье Итак, два пути – какой из них избрать? По-видимому, тот, который проще. Во всяком случае, в большинстве практических задач предпочтение отдается частотному направлению. Если ...
0 комментариев