Навигация
Ряды Фурье. Численные методы расчета коэффициентов
22876
знаков
13
таблиц
6
изображений
Курсовая работа студента гр. МТ-31
Нургалиев А. З.
Иновационный евразийский университет
Павлодар 2006 год.
1. Введение.В курсовой работе рассмотрено различные методы определения коэффициентов рядов Фурье. При разработки данного вопроса было рассмотрено тригонометрическая интерполяция теории и дискретное преобразование рядов Фурье. Также была разработана программа для расчетов коэффициентов на ЭВМ.
Целью этой работы является рассмотрение возможности разложения функции в ряд Фурье и актуальность применения этого разложения в инженерно-технических расчетах, оценить ее практическую и теоретическую значимость. Главной задачей является нахождение более оптимального решения задачи определения коэффициентов на ЭВМ, позволяющего минимизировать использование системных ресурсов, сократить время вычислений с наименьшей погрешностью.
2. Разложение периодической функции.
В науке и технике часто приходится иметь дело с периодическими явлениями , т.е. такими, которые воспроизводятся в прежнем виде через определённый промежуток времени Т, называемый периодом. Примером может служить установившееся движение паровой машины, которая по истечению определённого числа оборотов снова проходит через свое начальное положение., затем явление переменного тока и т. п. Различные величины, связанные с рассматриваемым периодическим явлением, по истечении периода Т возвращаются к своим прежним значениям и представляют, следовательно, периодические функции от времени t, характеризуемые равенством
Таковы например, сила и напряжение переменного тока или – пример паровой машины – путь, скорость и ускорение крейцкопфа, давление пара, касательное усилие в пальце кривошипа и т. д.
Простейшей из периодических функций (если не считать постоянной) является синусоидальная величина: 
, где 
есть «частота», связанная с периодом Т соотношением:
(1)
Из подобных простейших периодических функций могут быть составлены и более сложные. Наперед ясно, что составляющие синусоидальные величины должны быть разных частот, ибо, как легко убедится, сложение синусоидальных величин одной и той же частоты не дает ничего нового, поскольку приводит опять к синусоидальной величине, притом той же частоты. Наоборот, если сложить несколько величин вида
, 
, 
, 
, …, (2)
которые , если не считать постоянной, имеют частоты
, 2, 3, …,
кратные наименьшей из них, , и периоды
Т, 
, 
, …,
то получится периодическая функция (с периодом Т), но уже существенно отличная от величин типа (2).
Для примера мы воспроизводим здесь сложение трех синусоидальных величин:
;
график этой функции по своему характеру уже значительно разнится от синусоиды. Еще в большей степени это имеет место для суммы бесконечного ряда, составленного из величин вида (2).
Теперь естественно поставить обратный вопрос: можно ли данную периодическую функцию 
периода Т представить в виде суммы конечного или хотя бы бесконечного множества синусоидальных величин вида (2)? Как увидим ниже, по отношению к довольно широкому классу функций на этот вопрос можно дать утвердительный ответ, но только если привлечь именно всю бесконечную последовательность величин (2). Для функций этого класса имеет место разложение в «тригонометрический ряд»:
,
причем 
суть постоянные, имеющие особые значения для каждой такой функции, а частота дается формулой (1).
Геометрически это означает, что график периодической функции получается путем наложения ряда синусоид. Если же истолковать каждую синусоидальную величину механически как представляющую гармоническое колебательное движение, то можно также сказать, что здесь сложное колебание, характеризуемое функцией 
или просто ее гармониками (первой, второй и т. д.). Самый же процесс разложения периодической функции на гармоники носит название гармонического анализа.
Если за независимую переменную выбрать
,
то получится функция от x:
,
тоже периодическая, но со стандартным периодом 
. Разложение же (3) примет вид
. (4)
Развернув члены этого ряда по формуле для синуса суммы и положив
(n=1,2,3,…),
мы придем к окончательной форме тригонометрического разложения:
,
в которой мы всегда и будем его рассматривать. Здесь функция от угла x, имеющая период , оказывается разложенной по косинусам и синусам углов, кратных x.
Мы пришли к разложению функции в тригонометрический ряд, отправляясь от периодических, колебательных явлений и связанных с ними величин. Важно отметить, однако, уже сейчас, что подобные разложения часто оказываются полезными и при исследовании функции, заданных лишь в определенном конечном промежутке и вовсе не порожденных никакими колебательными явлениями.
Похожие работы
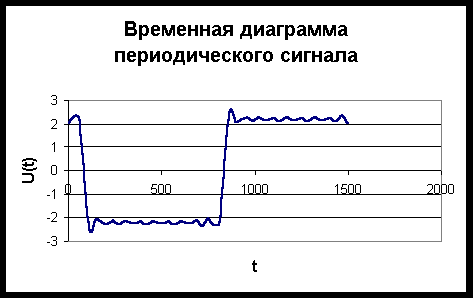
... . Сигнал задан в виде функции времени U(t) , повторяющийся с периодом Т. Требуется выполнить спектральный анализ сигнала и построить графики амплитудного и фазового спектров сигнала. 2.Численные методы расчетов спектральных и временных характеристик периодических сигналов Для расчета спектральных и временных характеристик периодического сигнала используем численные методы, чтобы упростить ...
... , либо функция задана таблично , нахождение интеграла по формуле Ньютона-Лейбница невозможно. Используют приближенные формулы, которые называют квадратурными, либо формулами численного интегрирования. 1) Формулы прямоугольника Пусть y=f(x) непрерывна на [a,b]. Требуется вычислить . Разобьем отрезок интегрирования на n равных частей, точками xi, i=0,n xi=a-i*h шаг ...
... для графа на рис. 3, приняв, что дерево образовано ветвями 2, 1 и 5 Ответ: B= Решить задачу 5, используя соотношения (8) и (9). Теория / ТОЭ / Лекция N 3. Представление синусоидальных величин с помощью векторов и комплексных чисел. Переменный ток долгое время не находил практического ...
... системам линейных алгебраических уравнений с более чем одной неизвестной; MATLAB решает такие уравнения без вычисле-ния обратной матрицы. Хотя это и не является стандартным математическим обозначением, система MATLAB использует терминологию, связанную с обычным делением в одномерном случае, для описания общего случая решения совместной системы нескольких линейных уравнений. Два символа деления / ...
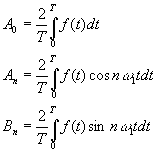
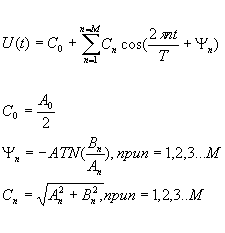
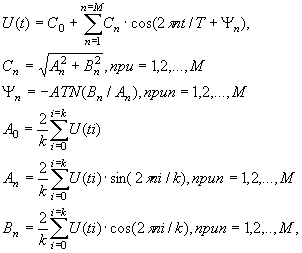
0 комментариев