Навигация
Генератор случайных чисел в Borland C++
7. Генератор случайных чисел в Borland C++
В языке C, как и во многих других языках высокого уровня, существует встроенная поддержка генератора случайных чисел. Для формирования чисел используется программный ГСЧ, существующий в программе в единственном экземпляре. Таким образом, с его помощью нельзя параллельно генерировать несколько независимых случайных последовательностей без специальных ухищрений. Тем не менее, одного ГСЧ достаточно для большинства прикладных задач.
В Borland C++ (как и во многих других реализациях C/C++) используется линейный конгруэнтный ГСЧ. Длина периода этого ГСЧ составляет 232 числа.
Для работы с ГСЧ в языке C предусмотрены следующие функции:
1) int rand()
Возвращает случайное целое число в диапазоне от 0 до RAND_MAX, где RAND_MAX – некоторая константа, зависящая от конкретной реализации ГСЧ. В Borland C++ значение RAND_MAX=32767.
2) int random (int max)
Возвращает случайное целое число в диапазоне от 0 до max‑1.
3) void srand (unsigned seed)
Устанавливает новое зерно ГСЧ. Обычно используется для установки известного начального значения x0 при отладке программы.
4) void randomize()
Устанавливает начальное значение, полученное из текущего системного времени путем путем преобразования его в целое число. Обычно используется для сброса ГСЧ в начале программы с целью предотвращения генерирования одних и тех же последовательностей. Не рекомендуется использовать в процессе отладки, т. к. последовательность, выбранную вызовом randomize(), сложно воспроизвести. Кроме того, не рекомендуется вызывать слишком часто или через фиксированные промежутки времени, т. к. это снизит качество («случайность») генерируемых последовательностей.
8. Практические задания
8.1 Случайные числа в заданном диапазоне
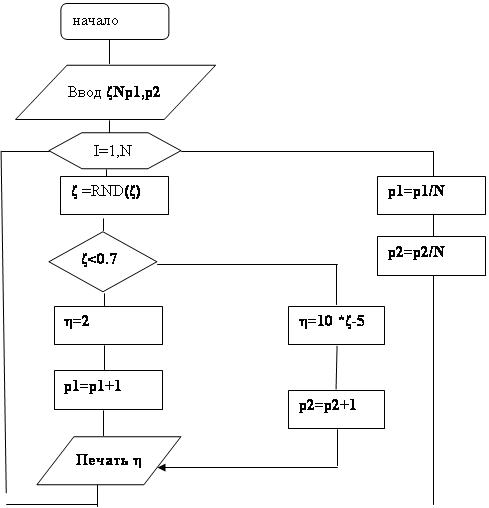
Выдайте на экран 10 случайных равномерно распределенных чисел в диапазоне:
1) От 3 до 12, целые.
2) Из множества {–3, 0, 6, 9, 12, 15}.
3) От 3 до 12, вещественные.
4) От –2,3 до 10,7 с шагом 0,1.
5) Из множества {–30; 10; 63; 59; 120; 175}.
6) Из множества {1; 0,1; 0,01; …; 10–15}.
8.2 Двумерные случайные величины
Написать функцию генерации случайной точки в двумерном круге с параметрами r, x0, y0.
8.3 Генерация одномерной случайной величины
Постройте случайную последовательность плотностью распределения которой принимает значение 1/4 на отрезке [0; 2] и 1/2 на отрезке [4; 5].
8.4 Оценить вероятность
В урне 5 белых, 10 черных и 15 красных шаров. Вынимают три шара. Оцените программным способом вероятность того, что все шары разного цвета.
8.5 Медианы треугольника
Известно, что две медианы в треугольнике пересекаются в точке, которая делит их в отношении 2:1. Используя ГСЧ и векторную алгебру, докажите этот факт.
9. Лабораторные задания
9.1 ГСЧ фон Неймана
Реализуйте программно метод средин квадратов для двоичных 8-разрядных чисел. Покажите, что ГСЧ зацикливается после прихода в ноль.
Замечания:
1. Квадрат числа будет занимать 16 бит, что может вызвать переполнение знакового типа int. Рекомендуется использовать типы unsigned int или long для промежуточных вычислений.
2. Для выделения средней части следует использовать операции сдвига и преобразования типа (либо побитового «И»).
9.2 Случайная матрица
Заполните динамическую матрицу 40×50 целыми случайными числами от –3 до 2. Найдите среднее арифметическое всех элементов этой матрицы. Зная точное значение данной величины (![]() ), вычислите ее относительную погрешность (в процентах) по формуле:
), вычислите ее относительную погрешность (в процентах) по формуле:
100% * (ТочноеЗначение – ПриблЗначение) / ДлинаДиапазона
Замечания:
1. Количество целых чисел в диапазоне от –3 до 2 равно 2 – (–3) + 1 = 6.
2. Чтобы напечатать символ %, используйте в функции printf спецификатор «%%».
9.3 Площадь фигуры
С помощью встроенного ГСЧ вычислите площадь фигуры, ограниченной линиями:
2 ≤ x ≤ 5,
4 ≤ y ≤ 25,
y ≤ x2.
Вычислите относительную погрешность (в процентах) в двух случаях, когда количество случайных точек равно 1000 и 10000.
Замечания: точное значение площади в данном примере равно
125/3 – 8/3 – 12
9.4 Случайная величина с заданными свойствами
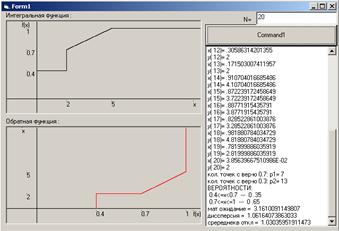
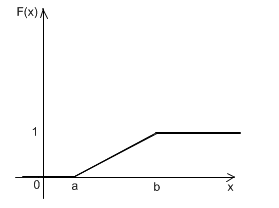
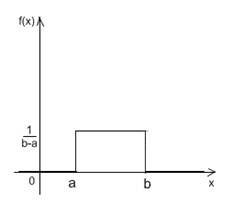
Напишите функцию, генерирующую случайные числа с заданным распределением методом обратной функции распределения.
Распределения, для которых требуется генерировать случайные числа:
1. Равномерное на отрезках [a, b] È [c, d].
2. Треугольное с параметрами [a, b].
10. Дополнительные задания
10.1 Многомерные случайные величины
Напишите функцию генерации случайной точки в n‑мерном шаре с центром в начале координат и радиусом r.
10.2 Быки и коровы
Напишите программу, моделирующую игру «Быки и коровы». Программа выбирает с помощью датчика случайных чисел четырехзначное число с разными цифрами. Цель игры – угадать это число. На каждом шаге играющий называет четырехзначное число, а программа сообщает, сколько цифр числа угадано (быки) и сколько угаданных цифр стоит на нужном месте (коровы).
Библиографический список
1. Керниган Б. Язык программирования Си: Задачи по языку Си. / Б. Керниган, Д. Ритчи, А. Фьюэр М.: Финансы и статистика, 1985. – 192 с.
2. Керниган Б., Ритчи Д. Язык программирования Си. М.: Финансы и статистика, 1992. – 272 с.
3. Подбельский В.В., Фомин С.С. Программирование на языке Си. Учеб. пособие. М.: Финансы и статистика, 2004. 600 с.
4. Форсайт Дж. Машинные методы математических вычислений / Дж. Форсайт, М. Малькольм, К. Моулер. М.: Мир, 1980. – 279 с.
5. Кнут Д. Искусство программирования, том 2. Получисленные методы / Д. Кнут. М.: Изд. дом «Вильямс», 2007. 832 с.
6. Каханер Д. Численные методы и математическое обеспечение: Пер. с англ. / Д. Каханер, К. Моулер, С. Нэш. М.: Мир, 1998. – 575 с., ил.
7. Зубинский А. В поисках случайности // А. Зубинский. Компьютерное обозрение №29, 2003.
Похожие работы
... на выходах генератора формируются два числа (на выходе счётчика 2 и выходе сумматора 10). Первое из них соответствует нечёткому значению интервала времени, необходимого для достижения поставленной цели, а второе - нечёткому значению результата настройки. В отличие от известных предложенный метод (алгоритм) позволил создать простой по своей структуре генератор случайных чисел, у которого наработка
... η с функцией распределения F(y) из случайной величины ζ, равномерно-распределенной в интервале [0,1], используются различные методы. К основным методам моделирования случайных чисел с заданным законом распределения относятся: - метод обратной функции - метод отбора или исключения - метод композиции. 2. Метод обратной функции Если ζ- равномерно-распределенная на интервале ...
... величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока.2.2. Начало алгоритмизации. Для получения двух последовательностей из 50 случайных чисел с показательным и нормальным законами распределения необходимо организовать цикл, который будет выполнятся 50 раз. Внутри цикла будем пользоваться функцией из Турбо Паскаля ...
... нельзя в полной мере назвать случайными, поскольку между ними имеется зависимость, а также наличие периодов в последовательности псевдослучайных чисел. К алгоритмическим методам получения ГСЧ относиться метод серединных квадратов, предложенный в 1946 г. Дж. фон Нейманом. Метод серединных квадратов Имеется некоторое четырехзначное число R0. Это число возводится в квадрат и заносится в R1. Далее ...
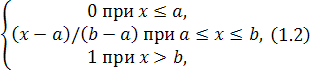
0 комментариев