Навигация
Моделирование датчиков случайных чисел с заданным законом распределения
Министерство Образования Республики Таджикистан
Таджикский Технический Университет
имени М.С. Осими
Кафедра «АСОИиУ»
Лабораторная работа №1
На тему: Моделирование датчиков случайных чисел с заданным законом распределения
Выполнила:
ст-т. 3-го курса гр. 2202 Б2
Принял: преподаватель кафедры
Ли И.Р.
Душанбе-2010
Лабораторная работа № 2
Моделирование датчиков случайных чисел с заданным законом распределения
I Цель работы
Целью работы является:
1. Практическое освоение методов моделирования случайных чисел с заданным законом распределения
2. Разработка и моделирование на ПЭВМ датчика случайных чисел с конкретным законом распределения
3. Проверка адекватности полученного датчика
II Теоретические сведения
1. Основные методы моделирования случайных последовательностей с заданным законом распределения
При исследовании и моделировании различных сложных систем в условиях действия помех возникает необходимость в использовании датчиков случайных чисел с заданным законом распределения. Исходным материалом для этого является последовательность x1,x2….xn с равномерным законом распределения в интервале [0,1]. Обозначим случайную величину, распределенную равномерно через ζ(кси).
Тогда равномерно-распределенные случайные числа будут представлять собой независимые реализации случайной величины ζ, которые можно получить с помощью стандартной функции RND (ζ)– программно реализованной на ПЭВМ в виде генератора случайных чисел с равномерным законом распределения в интервале [0,1]. Требуется получить последовательность y1,y2,..yn независимых реализаций случайной величины η, распределенных по заданному закону распределения. При этом закон распределения непрерывной случайной величины может быть задан интегральной функцией распределения:
F(y)= P(ksi![]() y) (1)
y) (1)
или плотностью вероятности
f(y)=F’(y) (2)
Функции f(y) и F(y) могут быть заданы графически или аналитически.
Для получения случайной величины η с функцией распределения F(y) из случайной величины ζ, равномерно-распределенной в интервале [0,1], используются различные методы. К основным методам моделирования случайных чисел с заданным законом распределения относятся:
- метод обратной функции
- метод отбора или исключения
- метод композиции.
2. Метод обратной функции
Если ζ- равномерно-распределенная на интервале [0,1] случайная величина, то искомая случайная величина может быть получена с помощью преобразования:
η=F-1 (ζ) (3)
Где F-1 (ζ) - обратная функция по отношению к функции распределения F(ζ)
![]() F(y)
F(y)

![]()
![]() 1
1
![]()
![]()
![]() ζ
ζ
![]()
![]() 0 η y
0 η y
Рис 1 Функция распределения F(ζ)
Действительно, при таком определении случайной величины η имеем:
P(η![]() y)=P{F-1(ζ)
y)=P{F-1(ζ)![]() y}=P{ ζ
y}=P{ ζ![]() F(y) }= F(y) (4)
F(y) }= F(y) (4)
В данной цепочке равенств первое равенство следует из (3), второе из неубывающего характера функций F(ζ) и F-1 (ζ) и третье из равномерного в интервале [0,1] распределения величин ζ.
Таким образом, если задана функция распределения F(y), то для получения случайной последовательности с таким распределением необходимо найти ее обратную функцию.
Для нахождения обратной функции можно использовать два метода: аналитический и графический.
3.Метод отбора или исключения
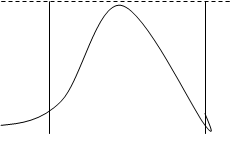
Данный метод удобнее использовать, если требуемый закон распределения задан плотностью вероятности f(y). В отличии от метода обратной функции метод отбора или исключения для получения одного требуемого случайного числа требует не одного равномерно- распределенного случайного числа, а двух, четырех, шести или более случайных чисел. В этом случае область возможных значений η представляет конечный отрезок (a,b), а плотность вероятности f(y) ограничена сверху значением fmax (Рис.7). Тогда область значений η* и ζ* можно ограничить ступенчатой кривой:
![]() 0, если y<a
0, если y<a
g(y)= fmax, если a ![]() y
y ![]() b (25)
b (25)
0, если y>b
Затем берутся с помощью генератора случайных чисел (RND(ζ)) два равномерно-распределенных числа ζ1 и ζ2 , по которым определяются равномерные на интервале [a,b] независимые величины:
η ’=a + (b-a)*ζ1
ζ’=fmax* ζ2 (26)
Где a,b – границы возможных значений случайной величины η,
fmax- максимальное значение функции f(y) (Рис.7)
![]() f(y)
f(y)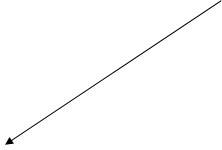
![]() g(y)
g(y)
![]() fmax
fmax
f(y)
ζ![]()
![]()
![]()
![]() a η ’ b
a η ’ b
Рис.7 Заданная плотность вероятности
Если ζ’ ![]() f (η ’) , то η ’ принимается в качестве очередной реализации случайной величины η. В противном случае η ’ отбрасывается и берется следующая пара равномерно- распределенных случайных чисел ζ1 и ζ2 . Такая процедура повторяется до тех пор, пока мы не получим требуемого количества случайных чисел с заданной плотностью вероятности.
f (η ’) , то η ’ принимается в качестве очередной реализации случайной величины η. В противном случае η ’ отбрасывается и берется следующая пара равномерно- распределенных случайных чисел ζ1 и ζ2 . Такая процедура повторяется до тех пор, пока мы не получим требуемого количества случайных чисел с заданной плотностью вероятности.
Похожие работы
... ;…≤ξn . Шаг 3. Нужные статистики вычисляются по формулам Kn+ = max ( - F(xj)); Kn- -= max (F(xj) - ), при 1≤j≤n. Заключение В данной курсовой работе рассмотрены вопросы применения случайных чисел для прикладных задач математики и информатики, рассмотрены методы получения случайных чисел, начиная от самых ранних методов с использованием первых вычислительных машин ...
... в серии опытов сходится по вероятности к рассчитанной теоретически вероятности данного события P(A) = 0.939. Распределение дискретной случайной величины по геометрическому закону распределения Моделирование случайной величины, имеющей геометрический закон распределения: (X=xk) = p(1-p)k где xk = k=0,1,2…, р – определяющий параметр, 0<p<1. Этот закон является дискретным. Составим ...
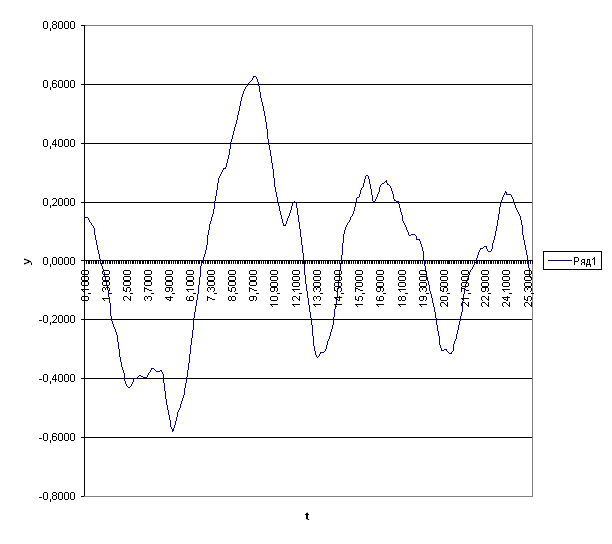
... - заданная функция: Рисунок 3 – Зависимость y от t Рисунок 4 – Зависимость z от t Заключение Была выполнена работа по моделированию состояния системы непрерывно-стохастической модели на ЭВМ, состояние которой описывается стохастическим дифференциальным уравнением , со следующими параметрами: где и - параметры спектральной плотности, , , и -коэффициенты уравнения, ...
... случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока. 2.2. Начало алгоритмизации. Для получения двух последовательностей из 50 случайных чисел с показательным и нормальным законами распределения необходимо организовать цикл, который будет выполнятся 50 раз. Внутри цикла будем пользоваться функцией из ...




0 комментариев