Навигация
Функция простого числа типа int
1. Функция простого числа типа int
int prost (int det)
{
int d, i, flag=1;
d=det;
if((d % 2==0 && d!=0 && d!=2) || d<0)
flag=0;
else
for (i=3; i<sqrt(d); i+=2)
if (d % i==0)
flag=0;
return flag;
}
Данная функция определяет, является ли число простым. Если функция получила простое число, то она возвращает единицу, в противном случае ноль.
Входные данные – число типа int.
Выходные данные – число типа int.
2. Функция проверки определителя и размерности матрицы.
int prov_data (int det, int a, int b, int n)
{
int flag;
if (det<a || det>b || n<2)
{
if (prost(det)==1 || n<2)
flag= -1;
}
else if (det==0)
flag= 0;
else if (det==1)
flag= 1;
else if (det>1 || (det<0 && det>a))
flag= 2;
return flag;
}
Если введенный определитель является простым числом, выходящим из введенного диапазона, и размерность меньше двух, то функция возвращает -1. Иначе если определитель равен нулю, то функция возвращает ноль. Иначе если определитель равен единице, то функция возвращает единицу, иначе если определитель больше двух или меньше нуля, то функция возвращает два.
Входные данные – четыре числа типа int.
Выходные данные – число типа int (-1, 0, 1 или 2).
3. Функция разложения числа на простые множители.
void faktor (int *mas_fakt, int det, int n)
{
int i, j=0, d, r;
int *mass1,*mass2;
mass1=(int*) malloc (n*sizeof(int));
mass2=(int*) malloc (n*sizeof(int));
if (det<0) d=-1*det;
else if (det>=0) d=det;
for (i=2; i<=d/2+1; i++)
{while (d % i==0)
{
d/=i;
*(mas_fakt+j)=i;
j++;
}
}
if (j<n)
{
while (j<=n)
{
*(mas_fakt+j)=1;
j++;
}
}
else if (j>n)
{
r=i=0;
while (i<j)
{
if (i<n)
*(mass1+i)=*(mas_fakt+i);
else if (i>=n)
{
*(mass2+r)=*(mas_fakt+i);
r++;
}
i++;
}
for (i=0; i<r; i++)
{j=*(mass2+i);
*(mass1+i)=*(mass1+i)*j;}
for (i=0; i<n; i++)
*(mas_fakt+i)=*(mass1+i);
}
if (det<0)
{r=*(mas_fakt+0);*(mas_fakt+0)=-1*r;}
free(mass1);
free(mass2);
}
В данной функции инициализируется цикл для разложения числа, массив mas_fakt заполняется значениями, полученными в результате разложения определителя на простые множители. Если размерность массива mas_fakt меньше размерности строки равной n генерируемой матрицы matr, дописываем единицами. Если размерность массива mas_fakt больше n, то используются два вспомогательных массива mass1 и mass2, где в массив mass1 записываются элементы 1, …, n из массива mas_fakt, а в массив mass2 все остальные. Потом элементы из массива mass1 умножаются на элементы из массива mass2. В итоге массив mas_fakt заполняется элементами массива mass1.
Входные данные – числа типа int.
Выходные данные – массив (mas_fakt) типа int.
4. Функция, генерации квадратной матрицы.
void gen_matric (int *matr, int *mas_fakt, int n, int a, int b)
{
int i, j,*vsp_mas, k=1, k1;
vsp_mas=(int*) malloc (n*sizeof(int));
for (i=0; i<n; i++)
for (j=0; j<n; j++)
{
if (i==j)
{
*(matr+i*n+j)=*(mas_fakt+j);
}
else if (i<j)
{
if (a>=-10 && b<=10)
*(matr+i*n+j)=random (b-a)+a; if (a<-10 || b>10)
*(matr+i*n+j)=random (b/4‑a/4)+a/4;
}
else *(matr+i*n+j)=0;
}
for (i=0; i<n; i++)
*(vsp_mas+i)=*(matr+0*n+i);
for (i=0; i<n; i++)
{
if (a<-10 || b>10)
{
k=random(7) – 3;
if (k1==k)
{
if (k<=3 && k>-3)
k-=1;
else if (k>=-3 && k<3)
k+=1;
}
}
for (j=0; j<n; j++)
{
if (i>0)
*(matr+i*n+j)=*(matr+i*n+j)+*(vsp_mas+j)*k;
else if (i==0)
*(matr+i*n+j)=*(matr+i*n+j);
}
k1=k;
}
free (vsp_mas);
}
Сначала инициализируется цикл для генерации треугольной матрицы, в которой массив mas_fakt располагается на главной диагонали, и одна из областей, находящаяся выше главной диагонали, заполняется случайными числами, принадлежащими введенному диапазону, а другая заполняется нулями. Потом инициализируется цикл для сложения первой строки, получившейся матрицы matr и умноженной на определенные коэффициенты, с остальными строками.
Входные данные – числа типа int.
Выходные данные – матрица (matr) типа int.
Листинг программы, реализующей алгоритм генерации матриц#include <conio.h>
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>
void gen_matric_0 (int *matr, int n, int a, int b);
void gen_matric_1 (int *matr, int n);
void gen_matric (int *matr, int *mas_fakt, int n, int a, int b);
int prov_data (int det, int a, int b, int n);
void print_matric (int *matr, int n);
void faktor (int *mas_fakt, int det, int n);
int prost (int det);
void main()
{
clrscr();
randomize();
FILE *fp;
int *matr, mas[4], det, k,*mas_fakt;
int n, i, j, l, l1, a, b;
int flag;
fp=fopen («inf.txt», «r»);
fseek (fp, 0L, SEEK_END);
l=ftell(fp);
fseek (fp, 0L, SEEK_SET);
printf («Входные данные:\n»);
i=0;
while (l!=ftell(fp))
{
fscanf (fp, «%d»,&k);
l1=ftell(fp);
mas[i]=k;
printf («%d:», mas[i]);
i++;
fseek (fp, l1, SEEK_SET);
}
fclose(fp);
det=mas[0];
n=mas[1];
a=mas[2];
b=mas[3];
matr=(int*) malloc (n*n*sizeof(int));
mas_fakt=(int*) malloc (n*sizeof(int));
faktor (mas_fakt, det, kol, n);
flag=prov_data (det, a, b, n);
if (flag==-1)
printf («\nПроверьте правильность ввода данных!\nРазмерность должна быть > или равно 2.\n Определитель должен входить в диапазон, \n если является простым числом, \n или раскладываться на простые множители принадлежащие данному диапазону!!!»);»);
else if (flag!=-1)
{
printf («\nМатрица:\n»);
if (flag==0)
gen_matric_0 (matr, n, a, b);
else if (flag==1)
{
gen_matric_1 (matr, n);
print_matric (matr, n);
printf («\n или\n\n»);
gen_matric (matr, mas_fakt, n, a, b);
}
else if (flag==2)
gen_matric (matr, mas_fakt, n, a, b);
print_matric (matr, n);
}
free (mas_fakt);
free(matr);
free(kol);
getch();
}
int prov_data (int det, int a, int b, int n)
{
int flag;
if (det<a || det>b)
{
if (prost(det)==1 || n<2)
flag= -1;
}
else if (det==0)
flag= 0;
else if (det==1)
flag= 1;
else if (det>1 || (det<0 && det>a))
flag= 2;
return flag;
}
void gen_matric_0 (int *matr, int n, int a, int b)
{
int *mass;
int nomer_str, i, j, k, l, ras;
mass=(int*) malloc (n*sizeof(int));
ras=n;
nomer_str=0;
if (n==2)
k=1;
else if (n>2)
k=2;
for (l=0; l<ras; l++)
mass[l]=a+random (b-a);
for (i=0; i<n; i++)
for (j=0, l=0; j<n; j++)
{
if (i==nomer_str)
{
*(matr+i*n+j)=mass[l];
l++;
}
else if (i==k)
{
*(matr+i*n+j)=mass[l];
l++;
}
else *(matr+i*n+j)=random (b-a)+a;
}
free(mass);
}
void gen_matric_1 (int *matr, int n)
{
int i, j;
for (i=0; i<n; i++)
for (j=0; j<n; j++)
{
if (i==j)
*(matr+i*n+j)=1;
else if (i!=j)
*(matr+i*n+j)=0;
}
}
void gen_matric (int *matr, int *mas_fakt, int n, int a, int b)
{
int i, j,*vsp_mas, k=1, k1;
vsp_mas=(int*) malloc (n*sizeof(int));
for (i=0; i<n; i++)
for (j=0; j<n; j++)
{
if (i==j)
{
*(matr+i*n+j)=*(mas_fakt+j);
}
else if (i<j)
{
if (a>=-10 && b<=10)
*(matr+i*n+j)=random (b-a)+a; if (a<-10 || b>10)
*(matr+i*n+j)=random (b/4‑a/4)+a/4;
}
else *(matr+i*n+j)=0;
}
for (i=0; i<n; i++)
*(vsp_mas+i)=*(matr+0*n+i);
for (i=0; i<n; i++)
{
if (a<-10 || b>10)
{
k=random(7) – 3;
if (k1==k)
{
if (k<=3 && k>-3)
k-=1;
else if (k>=-3 && k<3)
k+=1;
}
}
for (j=0; j<n; j++)
{
if (i>0)
*(matr+i*n+j)=*(matr+i*n+j)+*(vsp_mas+j)*k;
else if (i==0)
*(matr+i*n+j)=*(matr+i*n+j);
}
k1=k;
}
free (vsp_mas);
}
void print_matric (int *matr, int n)
{
int i, j;
for (i=0; i<n; i++)
{
for (j=0; j<n; j++)
{
printf («%5d»,*(matr+i*n+j));
}
printf («\n»);
}
}
void faktor (int *mas_fakt, int det, int n)
{
int i, j=0, d, r;
int *mass1,*mass2;
mass1=(int*) malloc (n*sizeof(int));
mass2=(int*) malloc (n*sizeof(int));
if (det<0) d=-1*det;
else if (det>=0) d=det;
for (i=2; i<=d; i++)
{
while (d % i==0)
{
d/=i;
*(mas_fakt+j)=i;
j++;
}
}
if (j<n)
{
while (j<=n)
{
*(mas_fakt+j)=1;
j++;
}
}
else if (j>n)
{
r=i=0;
while (i<j)
{
if (i<n)
*(mass1+i)=*(mas_fakt+i);
else if (i>=n)
{
*(mass2+r)=*(mas_fakt+i);
r++;
}
i++;
}
for (i=0; i<r; i++)
{
j=*(mass2+i);
*(mass1+i)=*(mass1+i)*j;
}
for (i=0; i<n; i++)
*(mas_fakt+i)=*(mass1+i);
}
if (det<0)
{r=*(mas_fakt+0);*(mas_fakt+0)=-1*r;}
free(mass1);
free(mass2);
}
int prost (int det)
{
int d, i, flag=1;
d=det;
if((d % 2==0 && d!=0 && d!=2) || d<0)
flag=0;
else
for (i=3; i<sqrt(d); i+=2)
if (d % i==0)
flag=0;
return flag;
Заключение
В заключение данной курсовой работы хотелось бы кратко сказать о проделанной работе, о проблемах, с которыми столкнулся при выполнении поставленной цели, и о перспективах развития и улучшения данного программного продукта.
Целью данной курсовой работы было составить алгоритм генерации матриц по введенному определителю, размерности и диапазона элементов матрицы.
Чтобы выполнить поставленную цель, необходимо было решить три задачи:
1. Поиск литературы по предмету данной курсовой работы.
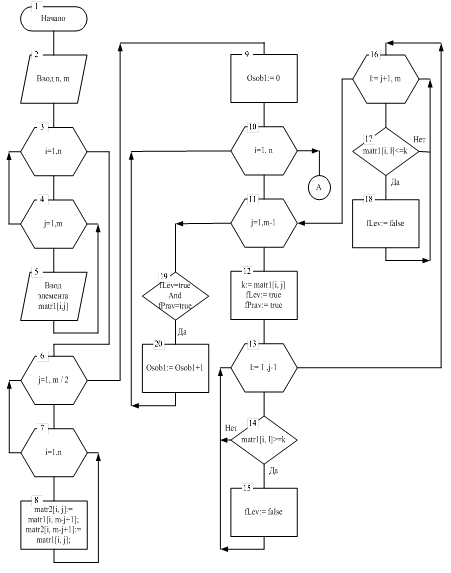
2. Составление алгоритма для выполнения поставленной цели.
3. Написание программы, реализующей составленный алгоритм.
При решении третьей задачи столкнулся с трудностью проверки корректности ввода данных. Необходимо было проверять, чтобы вводимый определитель удовлетворял диапазону элементов матрицы, т.е. введенный определитель, если является простым числом, то должен входить во введенный диапазон, и размерность матрицы должна быть больше двух.
Основными источниками, помогавшими выполнить поставленную цель, явились:
1. Книги по линейной алгебре, в которых содержался материал по теории матриц.
2. Книги по информатике и программированию.
Результатом данной курсовой работы стал алгоритм генерации матриц и написанная на его основе программа. Данная программа предназначена для работы с целыми числами. Одной из перспектив развития данного алгоритма является его улучшение для работы с действительными и комплексными числами, а программы – написание ее для работы со всеми числами: целыми, вещественными, комплексными.
Чтобы более полно использовать возможности алгоритма, его лучше реализовывать на тех языках программирования, у которых типы данных имеют достаточно большие диапазоны.
Надеюсь, что данная программа из области исследования при выполнении курсовой работы, при условии ее усовершенствования, выйдет в свет как полностью готовый к использованию программный продукт и будет востребован не только в целях методических разработок.
Список литературы
1. Ланкастер П. Теория матриц / Ланкастер П. – М.: Наука, 1982. – 272 с.
2. Линейная алгебра / Ильин В.А., Позняк Э.Г. – М.: Наука, 1978. – 304 с.
3. Кострикин А.И. Введение в алгебру / Кострикин А.И. – М.: Физико-математическая литература, 2001. – 368 с.
4. Писанецки С. Технология разряженных матриц / Писанецки С. – М.: Мир, 1988. – 410 с.
5. Гантмахер Ф.Р. Теория матриц / Гантмахер Ф.Р. – М.: Наука, 1988. – 552 с.
6. Подбельский В.В. Язык С++ / Подбельский В.В. – М.: Финансы и статистика, 2003. – 560 с.
7. Кетков Ю.Л., Кетков А.Ю. Практика программирования: Бейсик, Си, Паскаль. Самоучитель. / Кетков Ю.Л., Кетков А.Ю. – СПб.: БХВ – Петербург, 2002. – 480 с.
8. Мальцев А.И. Основы линейной алгебры / Мальцев А.И. – М.: Наука, 1970. – 400 с.
9. Крячков А.В., Сухинина И.В., Томшин В.К. Программирование на С и С++ / Крячков А.В., Сухинина И.В., Томшин В.К. – М.: Горячая линия – Телеком, 2000. – 344 с.
Приложение
Таблица тестов.
В таблице приведены результаты некоторых тестов программы.
| номер теста | входные данные | выходные данные |
| 1 | 0 2 -100 100 |
|
| 2 | -10 3 -50 50 |
|
| 3 | -1 3 -24 50 |
|
| 4 | 50 2 -100 100 |
|
| 5 | 113 4 -100 100 | Проверьте правильность ввода данных! Размерность должна быть > или равно 2. Определитель должен входить в диапазон, если является простым числом, или раскладываться на простые множители принадлежащие данному диапазону!!! |
| 6 | 1 3 -24 50 |
|
Похожие работы
... существуют такие конечные значения для Ui и Uj, что для маршрута, содержащего N городов, условие (4) удовлетворяется как неравенство или строгое равенство. А следовательно, модель (1-4) описывает задачу о коммивояжере. Описание программной реализации алгоритма В программе реализован классический вариант метода ветвей и границ, то есть алгоритм решения следующий: Все множество разбивается ...
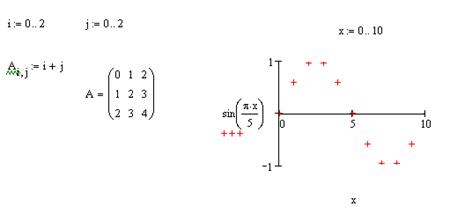
... с единицами измерений физических величин в системе MathCAD? 11. Подробно охарактеризуйте текстовые, графические и математические блоки. Лекция №2. Задачи линейной алгебры и решение дифференциальных уравнений в среде MathCAD В задачах линейной алгебры практически всегда возникает необходимость выполнять различные операции с матрицами. Панель операторов с матрицами находится на панели Math. ...
... с помощью логических операций. Оператор цикла В программировании постоянно возникают задачи, требующие для своего решения многократного повторения одной и той же последовательности действий или однообразной обработки однородных объемов информации (массивов). Например, когда требуется определить сумму всех элементов массива, найти его элемент с максимальным значением, вычислить квадраты всех ...
... матриц 10×10, для этого сделаем 20 попыток на каждое значение вероятности: ЗАКЛЮЧЕНИЕ В результате выполнения курсовой работы мною была разработана и отлажена программа, позволяющая находить кратчайшие покрытия булевых матриц размером до 100×100 методом Патрика (см. раздел 3.1) и методом Закревского (столбцовое и строчное покрытие) (см. раздел 3.2), а так же рассмотрен способ ...

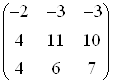

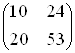
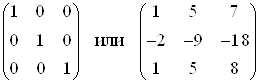

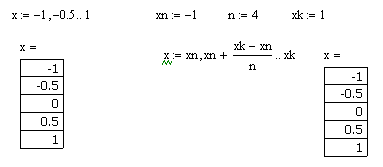
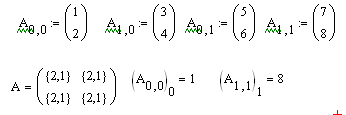





0 комментариев