Навигация
Часть программы, переводящая символ, являющийся цифрой, в число
6. Часть программы, переводящая символ, являющийся цифрой, в число.
{
w=s[i]-'0';
q=10*q+w;
x=1;
}
Если введенный символ – цифра, то из кода этого символа вычитаем из кода символа код нуля и получаем число, соответствующее введенному символу.
2.3 Листинг программы, реализующей алгоритм генерации полиномов#include <stdio.h>
#include <conio.h>
#include <math.h>
#include <string.h>
#include <ctype.h>
#include <stdlib.h>
#include <values.h>
#include <time.h>
long Modul(long a)
{
if (a<0) return (-a);
else return (a);
}
int provper(long a, long b)
{
if(b==0 || a==0) return(1);
else
if(Modul(a)<MAXLONG/Modul(b)) return(1);
else return(0);
}
int provsum(long a, long b)
{
if(Modul(a)<(MAXLONG-Modul(b))) return(1);
else return(0);
}
void peremnoz (long *a, int n, long *b, long *c) {
long z=0;
int i,j;
for ( i=0; i<n;i++)
for( j=0; j<2; j++)
{
if(provper(*(a+i),*(b+j))==1)
z=(*(a+i)*(*(b+j)));
else *(c+(i+j))=MAXLONG;
if(provsum(z,*(c+(i+j)))==1)
*(c+(i+j))+=z;
else *(c+(i+j))=MAXLONG;
}
}
int prov(long *a, int n)
{
int i, y=0;
for(i=0;i<n+1;i++)
if(Modul(*(a+i))==MAXLONG)y++;
return (y);
}
void main()
{
int stepen=0, n=2, w, x=0, i, k, f=1;
long *a, *b, *m, *c, q=0, z;
char *s;
s=(char *) calloc(900, sizeof(char ));
clrscr();
do{
printf("Введите степень не меньшую, чем 2 и не большую, чем 100:");
gets(s);
if(strlen(s)<1)
{
printf("\nНе было введено значения. Повторите ввод\n");
x=0;
}
if(strlen(s)>9)
{
printf("\nВведено более 9 символов. Повторите ввод\n");
x=0;
}
else
{
for( i=0;i<strlen(s); i++)
if (isdigit(s[i])!=0)
{
w=s[i]-'0';
q=10*q+w;
x=1;
}
else
{
printf("\nВведен символ или пробел. Повторите ввод\n");
x=0;
break;
}
stepen=q;
free(s);
s=(char *) calloc(900, sizeof(char ));
q=0;
w=0;
}
}while( stepen<2 || stepen>100 || x==0);
clrscr();
a=(long *) calloc(stepen+1, sizeof(long ));
b=(long *) calloc(2, sizeof(long ));
m=(long *) calloc((stepen)*2, sizeof(long ));
c=(long *) calloc(stepen+1, sizeof(long ));
for(i=0;i<stepen*2;i++)
{
if(i%2==0)
{
do{
q=0;
printf("Введите корень многочлена #%d ", (i/2)+1);
gets(s);
if(strlen(s)<1)
{
printf("\nНе было введено значения. Повторите ввод\n");
x=0;
}
if(strlen(s)>9)
{
printf("\nВведено более 9 символов. Повторите ввод\n");
x=0;
}
else
{
if(s[0]=='-')
for(k=1; k<strlen(s); k++)
if (isdigit(s[k])!=0)
{
w=s[k]-'0';
q=10*q+w;
x=1;
f=-1;
}
else
{
printf("\nВведен символ или пробел. Повторите ввод\n");
x=0;
break;
}
else
for( k=0; k<strlen(s);k++)
if (isdigit(s[k])!=0)
{
w=s[k]-'0';
q=10*q+w;
x=1;
f=1;
}
else
{
printf("\nВведен символ или пробел. Повторите ввод\n");
x=0;
break;
}
}
free(s);
s=(char *) calloc(900, sizeof(char ));
} while(x==0);
if(f==1)
{
*(m+i)=q;
q=0;
w=0;
*(m+i)=-*(m+i);
}
else
if(f==-1)
{
*(m+i)=q;
q=0;
w=0;
}
}
else *(m+i)=1;
}
for(i=0;i<2;i++)
{
*(a+i)=*(m+i);
*(b+i)=*(m+2+i);
}
for( k=0;k<stepen-1;k++)
{
peremnoz(a,n,b,c);
for( w=0; w<n+1; w++)
{
*(a+w)=*(c+w);
*(c+w)=0;
}
for(w=0;w<2;w++)
*(b+w)=*(m+(i*n)+w);
n++;
}
clrscr();
if(prov(a,stepen)!=0)
{
printf("\nПроизошел выход за диапазон типа.");
printf("\n\nПри следующем использовании данного программного продукта будьте осторожны с\n вводимыми значениями степени и корней");
printf("\n\nСпасибо, что пользовались моим прогаммным продуктом!:)");
printf("\n\nНажмите любую кнопку.");
}
else
{
printf("\Генериремый полином:\n");
printf("x^%d",stepen);
for(i=stepen-1;i>0;i--)
{
if(i==1)
if(*(a+i)==-1) printf("-x");
else
if(*(a+i)==1) printf("+x");
else
if(*(a+i)<0) printf("%ldx",*(a+i));
else
if(*(a+i)>0) printf("+%ldx",*(a+i);
else n++;
else
if(*(a+i)==-1) printf("-x^%d",i);
else
if(*(a+i)==1) printf("+x^%d",i);
else
if(*(a+i)<0)
printf("%ldx^%d",*(a+i),i);
else
if(*(a+i)>0)
printf("+%ldx^%d",*(a+i),i);
else n++;
}
if(a[0]<0) printf("%ld",a[0]);
else
if(a[0]>0) printf("+%ld",a[0]);
else n--;
printf("=0");
printf("\n\nСпасибо, что пользовались моим прогаммным продуктом!:)");
printf("\n\nНажмите любую кнопку.");
}
free(a);
free(b);
free(c);
free(m);
free(s);
getch();
}
Входные данные: числа типа long.
Выходные данные: числа типа long.
1. При введенных значениях степени и корней генерируемого полинома, не допускающих выход за диапазон типа long, – коэффициенты генерируемого многочлена с соответствующими степенями переменных.
2. При не корректно введенных значениях:
1. Если при вводе степени введено число меньше двух и больше 100, то выдается сообщение о не корректном вводе с просьбой повторить ввод заново.
2. Если не было введено значение степени или корня полинома, то выдается сообщение о не корректном вводе с просьбой повторить ввод заново.
3. Если было введено более девяти символов, то выдается сообщение о не корректном вводе с просьбой повторить ввод.
4. Если был введен символ или пробел, то выдается сообщение о не корректном вводе с просьбой повторить ввод.
5. Если произошел выход за диапазон типа long, то выдается сообщение о не корректном вводе с просьбой при следующем использовании данного программного продукта быть аккуратными при вводе степени генерируемого полинома и его корней, чтобы не допустить выход за диапазон используемого типа.
Результаты теста данного программного продукта можно увидеть в Приложении.
Заключение
В заключение данной курсовой работы хотелось бы кратко сказать о проделанной работе, о проблемах, с которыми столкнулся при выполнении поставленной цели, и о перспективах развития и улучшения данного программного продукта.
Целью данной курсовой работы было составить алгоритм генерации полиномов по введенной степени и корням и написать программу, реализующую этот алгоритм.
Чтобы выполнить поставленную цель, необходимо было решить три задачи:
1. Поиск литературы по предмету данной курсовой работы.
2. Составление алгоритма для выполнения поставленной цели.
3. Написание программы, реализующей составленный алгоритм.
При решении третьей задачи столкнулся с рядом трудностей:
1. Организацией ввода значений и проверки его корректности. Необходимо было проверять, чтобы введенные значения являлись только числами.
2. Организацией хранения введенных данных для удобного обращения к ним в ходе написания и работы программы.
3. Проверки, чтобы при работе программы не произошел выход за диапазон используемого типа.
Основными источниками, помогавшими выполнить поставленную цель, явились:
1. Книги по линейной алгебре, в которых содержался материал по теории полиномов.
2. Книги по информатике и программированию.
3. Курс лекций, прочитанных в рамках дисциплин «Программирование на языке Си», «Информатика», «Структуры и алгоритмы компьютерной обработки данных», «Алгебра и теория чисел».
Результатом данной курсовой работы стал алгоритм генерации полиномов и написанная на его основе программа. Данная программа предназначена для работы с целыми числами, хотя алгоритм является действенным и при работе с вещественными числами, а при некоторых его усовершенствованиях (организации работы с мнимой частью) и с комплексными. Следовательно, одной из перспектив развития данного алгоритма является его улучшение для работы с комплексными числами, а программы – написание ее для работы со всеми числами: целыми, вещественными, комплексными.
Так же реально улучшить временную характеристику алгоритма и программы, если после проверки «не вышло ли произведение или сумма коэффициентов многочлена» за диапазон типа, если все же выход произошел, сразу же остановить работу алгоритма и программы и выдать пользователю сообщение об ошибке.
Чтобы более полно использовать возможности алгоритма, его лучше реализовывать на тех языках программирования, у которых типы данных имеют достаточно большие диапазоны.
Решив последнюю задачу, можно сразу решить такие задачи, как увеличение вводимого значения степени генерируемого полинома и количества вводимых символов и буфера.
Не трудно заметить, что при перемножении вещественных чисел с дробной частью количество цифр в дробной части их произведения будет равно, в общем случае, сумме количества символов перемножаемых чисел, поэтому количество символов в дробной части произведения при большом количестве символов в дробной части перемножаемых чисел достаточно быстро увеличивается.
Следовательно, одной из серьезнейших проблем при работе с вещественными и комплексными числами встает проблема точности, которую, в принципе на все сто процентов разрешить никогда не удастся, так как программист всегда будет ограничен в ресурсах, поэтому представить вещественные можно только лишь с определенной точностью, иногда вполне достаточной.
Надеюсь, что мой опыт в разработке подобных программных продуктов будет полезен другим людям, и данная программа из области исследования при выполнении курсовой работы, при условии, конечно же, его усовершенствования, выйдет в свет как полностью готовый к использованию программный продукт и будет востребован не только в целях методических разработок.
Список использованных источников и литературы
1. КурошА.Г. Курс высшей алгебры / А.Г. Курош. – М.: Наука, 1968. – 431с.
2. Шафаревич И.Р. Основные понятия алгебры / И.Р. Шафаревич. – Ижевск: Ижевская республиканская типография, 1999. – 348с.
3. Варден ван дер Б.Л. Алгебра / Б.Л. ван дер Варден. – М.: Наука, 1979. – 623с.
4. Математика. Большой энциклопедический словарь / Гл. ред. Ю.В. Прохоров. – 3-е изд. – М.: Большая Российская энциклопедия, 1998. – 848 с.: ил.
5. Подбельский В.В. Язык Си++: Учебное пособие. – 5 –е изд. / В.В. Подбельский. – М.: Финансы и статистика, 2003. – 560с.: ил.
6. Устян А.Е. Методические материалы по курсу «Алгебра и теория чисел» для студентов – государственников / А.Е. Устян. – Тула: Тул.гос.пед.ун –т им. Л.Н. Толстого, 1992. – 86с.
7. Зарисский О. Коммутативная алгебра. Том I / О. Зарисский, П. Самюэль. – М.: Издательство иностранной литературы, 1963. – 371с.
8. Ленг С. Алгебра / С. Ленг. – М.: Наука, 1999. – 564с.
Приложение
Таблица тестов
В таблице приведены результаты некоторых тестов программы.
Обратите внимание на то, что в скобках показаны некорректно введенные данные и сообщения программы об ошибках с просьбами повторить ввод.
| номер теста | входные данные | выходные данные |
| 1 | 2; 1, 2 | x^2-3x+2=0 |
| 2 | 3; 1, 2, 3 | x^3-6x^2+11-6=0 |
| 3 | 10; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 | x^10-10x^9+45x^-120x^7+210x^6- -252x^5+210x^4-120x^3 + 45x^2-10x+1 |
| 4 | 4; 1234, 4321, 23 ,32 | Произошел выход за диапазон типа |
| 5 | 2; 999999999, 1 | x^2-10000000000x+999999999 |
| 6 | 2; 0 , 0 | x^2=0 |
| 7 | (-4),(1), 3; (q), ( ), 0, 1, 100 | (Введен символ или пробел повторите ввод), (Введите степень не меньшую, чем 2, и не большую, чем 100), (Введен символ или пробел повторите ввод), (Не было введено значения), x^3-101x^2+100x=0 |
| 8 | 5; -1, 1, -2, 2, 0 | x^5-5x^3+4x=0 |
| 9 | 10; 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 | x^10-45x^9+870x^8-9450x^7+63273x^6- -269325x^5+723680x^4-1172700x^3+ +1026576x^2-362880x |
| 10 | 25; 1, 2, 3, 4, 5, 6, 7, 8, 9, 9, 8, 7, 6, 5, 4, 3, 2, 1, 1, 2, 3, 4, 5, 6, 7 | Произошел выход за диапазон типа |
Похожие работы
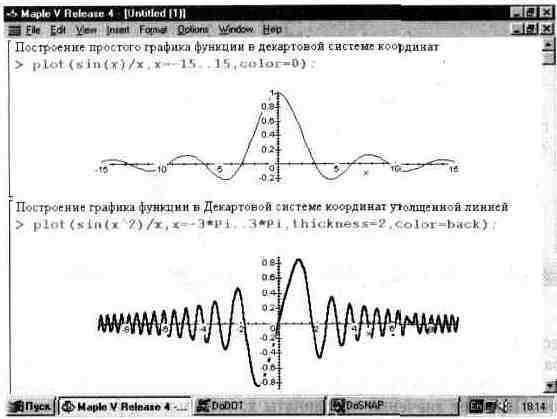
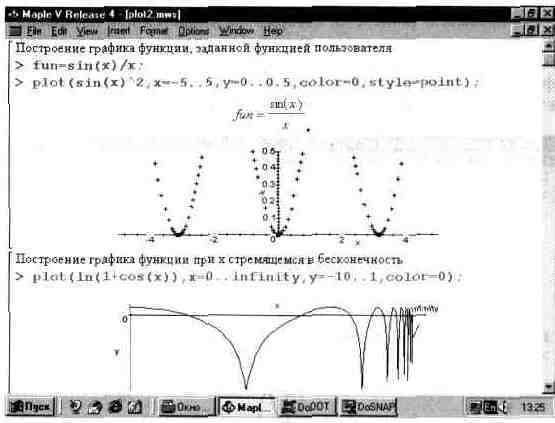
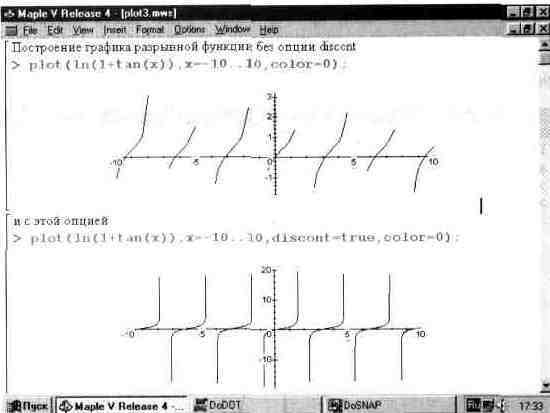
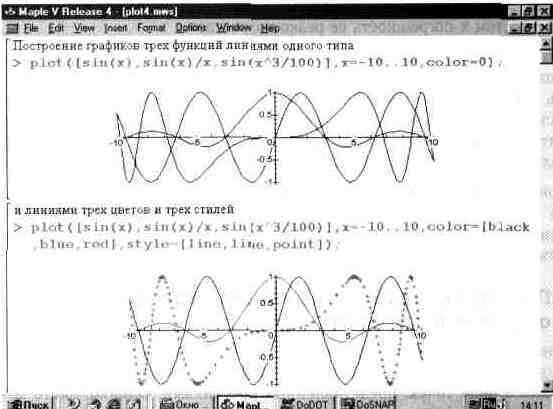
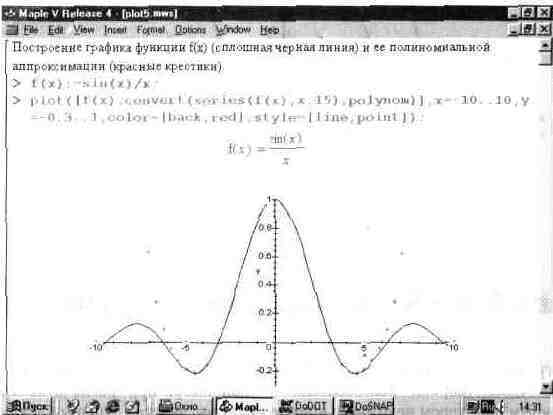
... типа MESH. 13.6. Графика пакета plots 13.6.1. Общая характеристика пакета plots Пакет plots содержит почти полсотни графических функции, существенно расширяющих возможности графики системы Maple V. В реализации R4 этот пакет содержит следующие функции: ——————————— animate Создает мультипликацию 2D графиков функций. animated Создает мультипликацию 3D графиков функции. changecoords ...
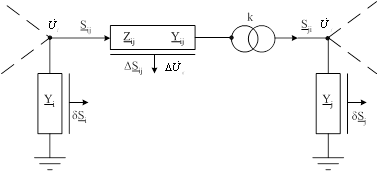
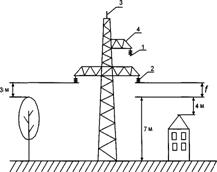
... Еловка ТМН-2500/35 ±6×1,5% Ужурсовхоз ТМН-4000/35 ±6×1,5% 2. Характеристика задачи расчета, анализа и оптимизации режимов РЭС 110-35 кВ по напряжению, реактивной мощности и коэффициентам трансформации Питающие электрические сети напряжением 110 кВ, ...
... мальне значення показникунадійності, при якому приймається рішення про орєінтованийзвязок назвем порогом показника надійності і позначимо (). Для можливості порівняння результатів у різних парах змінних в одній задачі системного синтезу корисно ввести відносний показник надійності. Відносним показником надійності ηij приняття рішення про напрям звязку між змінними xj → xi (стрілка в ...
... luc – программа используется для разложения матрицы на треугольные сомножители; rluc – программа, которая отвечает за решение системы уравнений. 4. Разработка адаптивной системы управления режимами электропотребления 4.1 Функции автоматизированной системы Сбор, накопление и передача информации, характеризующей режим электропотребления комбината (информация о нагрузках). Сбор, накопление ...


0 комментариев