Навигация
2 Алгоритм Методу
Формула Гаусса називається формулою найвищої алгебраїчної точності. Для формули розрахунку найвища точність може бути досягнута для поліномів степеня (2n-1), які визначаються 2n постійними ti і Ai (і=1,2,...,n).
Суть методу полягає у визначенні коефіцієнтів Ai і абсцис точок ti. Для знаходження цих постійних розглянемо виконання формули розрахунку для функцій вигляду (2.1):
f(t)=tk, k=0,1,…,2n-1. (2.1)
Враховуючи (2.2)
![]() tkdt=
tkdt=![]() , (2.2)
, (2.2)
отримаємо систему рівнянь (2.3) [4] :
![]() Ai=2;
Ai=2;
![]() Aiti=0;
Aiti=0;
![]() Aiti2=1; (2.3)
Aiti2=1; (2.3)
![]() Aiti2n-2=
Aiti2n-2=![]() ;
; ![]() Aiti2n-1=0;
Aiti2n-1=0;
Ця система нелінійна, і її звичайне розв'язання пов'язане із значними обчислювальними труднощами. Але якщо використовувати систему для поліномів вигляду (2.4):
f(t)=tkPn(t), k = 0,1,…,n-1, (2.4)
де Pn(t) - поліном Лежандра, тоді її можна звести до лінійної відносно коефіцієнтів Ai з заданими точками ti. Оскільки степені поліномів в співвідношенні не перевищують 2n-1, повинна виконуватися система і дана формула приймає вигляд (2.5) :
![]() tkPn(t)dt=
tkPn(t)dt=![]() AitikPn(ti) (2.5)
AitikPn(ti) (2.5)
В результаті властивості ортогональності ліва частина виразу дорівнює 0, тоді формула буде (2.6) : ![]() AitikPn(ti)=0, (2.6) що завжди забезпечується при будь-яких значеннях Ai в точках ti, які відповідають кореням відповідних поліномів Лежандра.
AitikPn(ti)=0, (2.6) що завжди забезпечується при будь-яких значеннях Ai в точках ti, які відповідають кореням відповідних поліномів Лежандра.
Підставляючи ці значення ti в систему і враховуючи перші n рівнянь, можна визначити коефіцієнти Ai.
Формула розрахунку, де ti - нулі полінома Лагранжа Pn(t), а Ai, i=1,2,...,n визначаються із системи, називається формулою Гаусса.
Значення Ai, ti для різних n наведені в довідниках.
Для довільного Інтервалу (а,b) формула для методу Гаусса приймає вигляд (2.7) :
I=![]()
![]() Aif(xi), (2.7)
Aif(xi), (2.7)
де xi обчислюється за формулою (2.8) :
xi=![]() +
+![]() ti. (2.8)
ti. (2.8)
Оцінка похибки формули Гаусса з n вузлами визначається із співвідношення (2.9) :
![]() (2.9)
(2.9)
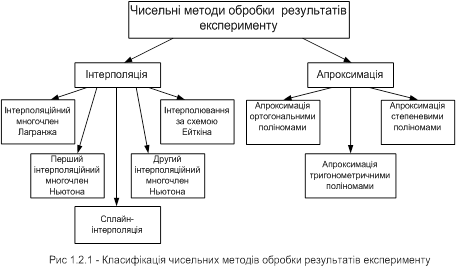
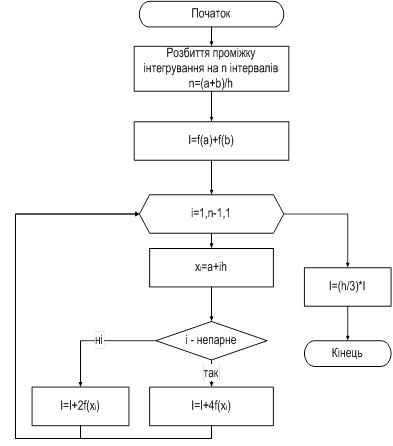
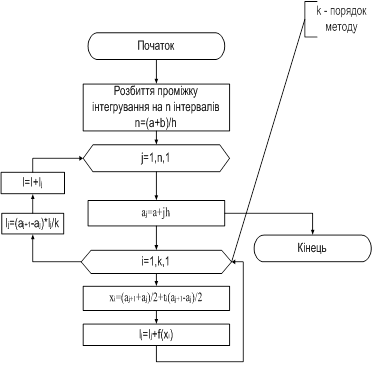
де M2n- максимальне значення 2n похідної на ділянці (а,b). Враховуючи наведені вище формули розробимо алгоритм методу (рис 1) [4].
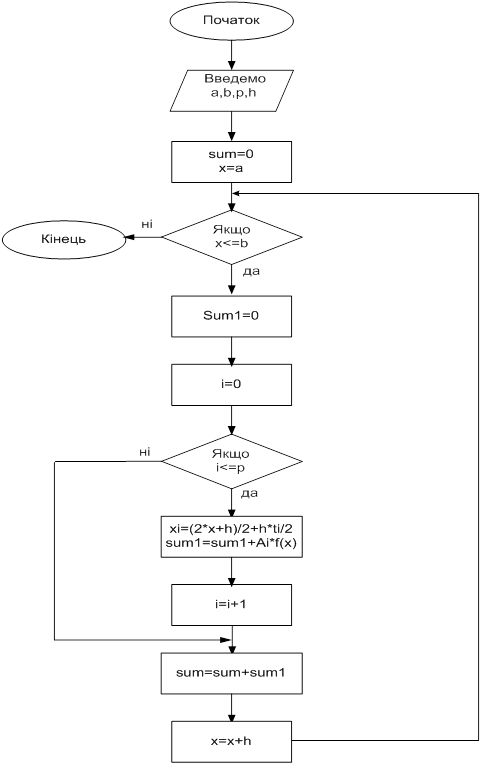
Рисунок 1 - Алгоритм методу Гауса
3 Загальні відомості та функціональні призначення
Дана програма обчислює інтеграл виду
I=![]() ,
,
методом Гауса третього, четвертого та п’ятого порядків. При зменшенні кроку інтегрування похибка обчислювань зменшиться.
Програма досить зручна та проста у користуванні. Результати обчислень виводяться на екран монітора разом із розв’язком, отриманим в математичному пакеті MathCAD 2001 Professional та похибкою обчислень .
Програма призначена для обчислення тільки одного інтегралу, що значно зменшує сферу її використання. Але змінивши програмний код можна досягти обчислення і кількох інтегралів.
Дана програма досить швидко проводить обрахунок і виводить відповідь безпосередньо на екран монітору.
Програма складена на Borland C++ 5.02 і для обчислення інтегралу методом Гауса третього, четвертого та п’ятого порядків потребує такі наступні системні параметри:
- Процесор типу Pentium-2;
-256 Мb ОЗУ;
-Операційні системи MS-Windows 98/95/ХР
-Video пам’ять 32 Мб.
Вхідними даними для програми є:
а) Межі інтегруваня: a = 0, b = 1;
б) Крок інтегрування: h = 0,1; 0,2; 0,5;
в) Підінтегральна функція :
f(x) = ![]() ;
;
Вихідними результатами є:
Наближене значення інтегралу отримане за допомогою Mat-hcad2001;
Результат інтегралу
I=![]()
на проміжку [0;1]
Відносна похибка при обрахунках .
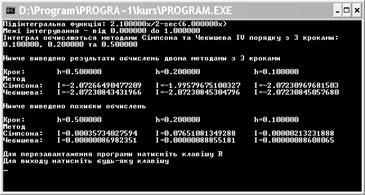
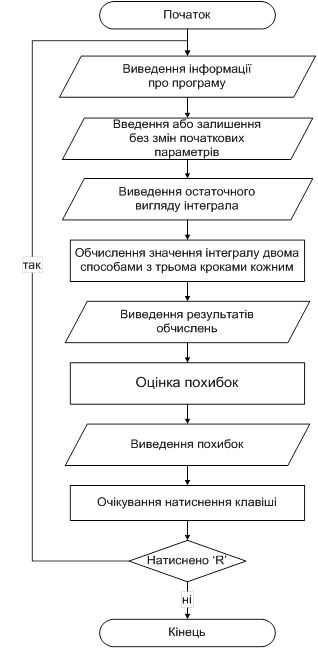
Результат виконання програми рисунок 2 буде мати такий вигляд:
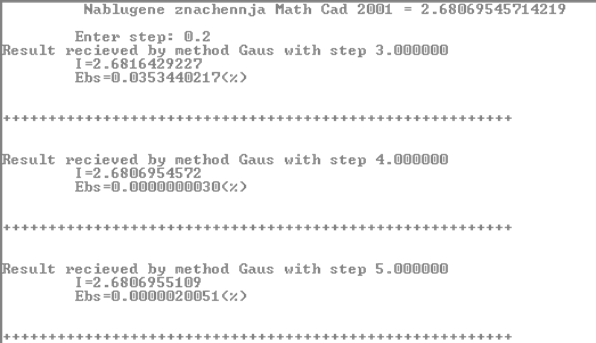
Рисунок 2 – Результат виконання програми
Розв’яжемо задачу в пакеті MathCAD 2001 Professional:
![]()
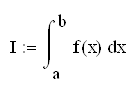
Значення інтегралу І=2,680695
Похожие работы
... функцію задано аналітичнo, але її вираз досить складний і незручний для виконання різних математичних операцій (диференціювання, інтегрування тощо). 2 Розробка алгоритмів моделювання зміни температури термопари за допомогою чисельних методів на ЕОМ 2.1 Планування вхідних та вихідних даних Для розв’язання поставленої задачі потрібні певні вхідні данні, на основі яких будуть проводитись ...
... програми Mathcad, рівне – 2,681. Нижче наведено результат роботи програми. Висновки В ході виконання даної курсової роботи було розглянуто методи чисельного інтегрування, а саме: Чебишева та Трапеції. Було досліджено вказані методи інтегрування та порівняно їх точності, розроблено програму на компіляторі Turbo C++, яка знаходить чисельне значення вказаного інтегралу. Таким чином були ...
... випадків, аварій, а з цим і простоїв на підприємстві, укріпити та створити культуру трудової діяльності. Виконання та розробка дипломного проекту “ Розробка дослідження системи керування електроприводом змінного струму дизель-потягу з використанням нейронних мереж ” відбувається за допомогою комп'ютера, тому питання охорони праці розглядаються щодо забезпечення здорових і безпечних умов роботи ...
... прийнятної точності необхідна велика кількість статистичних випробувань. Теорія методу Монте-Карло вивчає способи вибору випадкових величин для вирішення різних завдань, а також способи зменшення дисперсії випадкових величин. 3. Програма обчислення кратного інтеграла методом Монте-Карло Обчислити певний інтеграл . за методом “Монте-Карло” по формулі , де n – число випробувань ;g(x) – щі ...

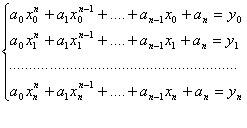


0 комментариев