Вхідні та вихідні дані

3.2 Вхідні та вихідні дані

 

Для розробленої програми вхідними даними є межі інтегрування a та b, а також множники біля змінної інтегрування x, c та d. Всі дані мають тип extended.

Вихідними даними являється чисельне значення інтегралу, обчислене методами Трапеції та Чебишева, причому кожним методом інтеграл обчислюється з 3 кроками. Також вихідними даними являються похибки, обчислені для кожного знайденого значення.

3.3 Структура програми

 

Програма, написана для вирішення поставленої задачі, містить кілька підпрограм. Спочатку програма виводить загальні відомості про своє призначення, потім пропонує змінити деякі параметри, після чого виконує обчислення інтегралу згаданими вище методами з кроками 0.1, 0.2 та 0.5. Підінтегральна функція для зручності міститься у функції f. Для обчислення інтегралу методом Сімпсона використовується функція Simpson, що приймає в якості параметрів межі інтегрування та крок обчислення. Для обчислення інтегралу методом Чебишева використовується дві функції: Chebushev та difChebushev. Функція Chebushev викликається безпосередньо з основної програми. Вона ділить межі інтегрування на проміжки, за величиною рівні кроку h, викликає функцію difChebushev для обчислення інтегралу на кожному проміжку, після чого сумує отримані значення, вираховуючи значення інтегралу. Потім основна програма виводить отримані значення на монітор, після чого для кожного значення вираховує похибку і виводить її на монітор.

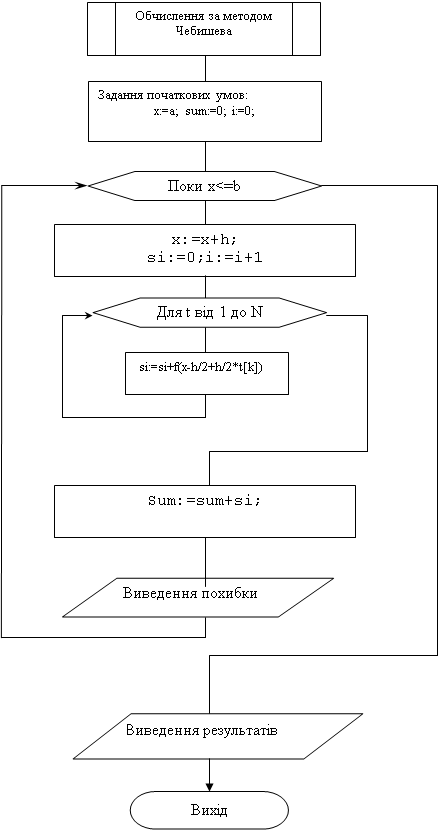
Блок-схему програми наведено в додатку Б.

 

3.4 Інструкція користувачеві

 

Для запуску програми необхідно запустити на виконання файл program.exe.

Розроблена програма інтуїтивно зрозуміла користувачеві. Перша дія, яку потрібно виконати користувачеві – проглянути параметрі та при необхідності в момент, коли програма запропонує змінити деякі параметри, натиснути клавішу ‘Y’ та ввести потрібні значення параметрів. Після цього програма виводить на монітор обчислені значення інтегралу. Користувачеві потрібно лише використати ці значення в своїх цілях. В кінці програма пропонує або вихід, або перезавантаження для повторного розрахунку. Якщо користувачеві потрібно обчислити ще один інтеграл, необхідно натиснути клавішу ‘R’.

4. Аналіз результатів розрахунку

Як видно з похибок програма дає досить точні результати обчислень. Отримані дані підтверджують, що обчислення методом Чебишева дають результат, який за точністю на кілька порядків перевищує точність методу Трапеції. Значення інтегралу, обчисленого за допомогою програми Mathcad, рівне – 2,681.

Нижче наведено результат роботи програми.

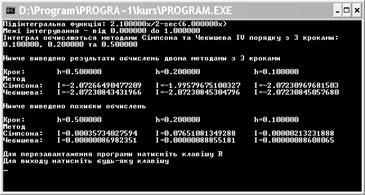
Висновки

 

В ході виконання даної курсової роботи було розглянуто методи чисельного інтегрування, а саме: Чебишева та Трапеції. Було досліджено вказані методи інтегрування та порівняно їх точності, розроблено програму на компіляторі Turbo C++, яка знаходить чисельне значення вказаного інтегралу. Таким чином були набуті практичні навички програмування задач, які ставить курс «Обчислювальні методи та застосування ЕОМ».

Література

 

1.         Квєтний Р.Н. Методи Комп’ютерних обчислень. - Навчальний посібник. - Вінниця: ВДТУ, 2001. - с. 92

2.         Волков Е. А. Численные методы. - М.: Наука, 1982. - с. 102.

3.         Самарский А.А., Гулин А.В. Численные методы. - М: Наука, 1989. - с. 161.

4. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. - Численные методы. - М: Наука, 1987. - с. 83

 

Додатки

 

Додаток А

 

Алгоритми методів

 

Алгоритм методу Сімпсона

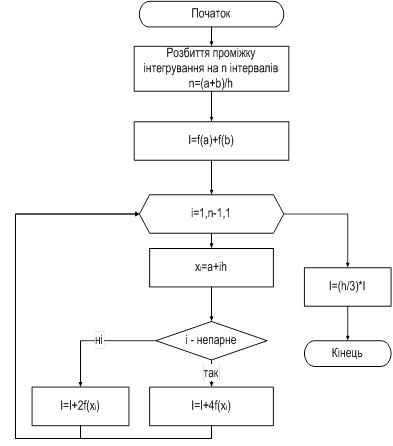
Алгоритм методу Чебишева

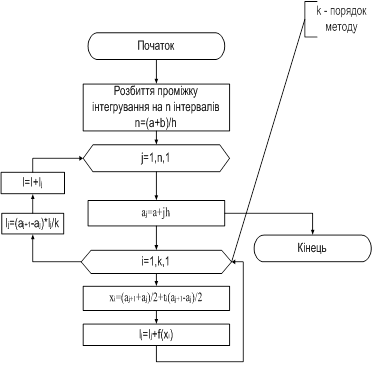
Додаток Б

 

Блок-схема програми

 

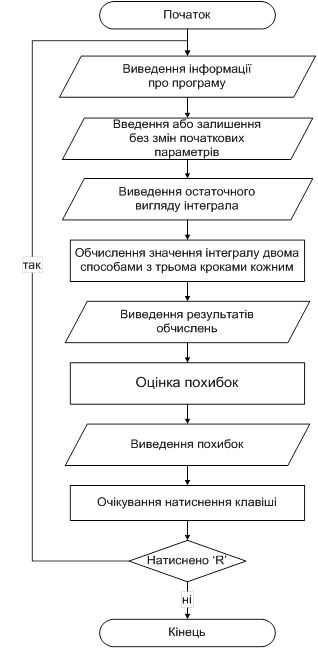
Додаток В

 

Лістинг пргорами

{$N+,E+}

program integral;

uses CRT, graph;

const h1=0.1; h2=0.2; h5=0.5;

var

a, b, c, d, sharp: extended;

ch: char;

res: array [1..2,1..3] of extended;

delta: array [1..2,1..3] of extended;

i, j: integer;

label

lbl1;

{------------------------------------------------}

function f (x: extended): extended;

begin

f:=c*x/2-d/(exp(x)+exp(-x)); {sec(d*x)=d/(exp(x)+exp(-x))}

end;

{------------------------------------------------}

function Simpson (a, b, h: extended): extended;

var

I, x: extended;

j: integer;

begin

I:=0; x:=a+h; j:=0;

I:=f(a)+f(b);

while (x<b-0.000001) do

begin

j:=j+1;

if ((j mod 2) = 0) then

I:=I+2*f(x)

else

I:=I+4*f(x);

x:=x+h

end;

Simpson:=I*h/3;

end;

{------------------------------------------------}

function difChebushev (a, b: extended): extended;

const

t4:array [1..4] of extended = (-0.794654, -0.187592, 0.187592, 0.794654);

n=4;

var

x, I: extended;

j: integer;

begin

I:=0;

for j:=1 to 4 do

begin

x:=(a+b)/2+t4[j]*(b-a)/2;

I:=I+f(x);

end;

difChebushev:=I*(b-a)/n;

end;

{------------------------------------------------}

function Chebushev (a, b, h: extended): extended;

var

I, x: extended;

j: integer;

begin

j:=0; I:=0; x:=a;

while (x<b-0.000001) do

begin

I:=I+difChebushev(x,x+h);

x:=x+h;

j:=j+1;

end;

Chebushev:=I

end;

{------------------------------------------------}

BEGIN

lbl1:

clrscr;

c:=2.1; d:=6;

a:=0; b:=1;

textmode (3);

textcolor(15);

writeln ('Програма обчислюэ iнтеграл функцii cx/2-sec(dx) в межах вiд a до b двома');

writeln ('методами: Сiмпсона та Чебишева IV порядку');

writeln ('Поточнi значення параметрiв:');

writeln ('a=', a:2:6);

writeln ('b=', b:2:6);

writeln ('c=', c:2:6);

writeln ('d=', d:2:6);

writeln ('Ви хочете змiнити параметри a та b? (y - так, iнша клавiша - нi)');

ch:=readkey;

if ((ch='y') or (ch='Y')) then

begin

write ('a=');

readln (a);

write ('b=');

readln (b);

end;

writeln ('Ви хочете змiнити параметри c та d? (y - так, iнша клавiша - нi)');

ch:=readkey;

if ((ch='y') or (ch='Y')) then

begin

write ('c=');

readln (c);

write ('d=');

readln (d);

end;

clrscr;

writeln ('Пiдiнтегральна функцiя: ', c:2:6, 'x/2-sec(', d:2:6, 'x)');

writeln ('Межi iнтегрування - вiд ', a:2:6, ' do ', b:2:6);

writeln ('Iнтеграл обчислюэться методами Сiмпсона та Чебишева IV порядку з 3 кроками: ');

writeln (h1:2:6, ', ', h2:2:6, ' та ', h5:2:6);

writeln;

write ('Виконуються обчислення.');

res[2,1]:=Chebushev(a, b, h1);

write ('.........');

res[2,2]:=Chebushev(a, b, h2);

write ('.........');

res[2,3]:=Chebushev(a, b, h5);

write ('.........');

res[1,1]:=Simpson(a, b, h1);

write ('.........');

res[1,2]:=Simpson(a, b, h2);

write ('.........');

res[1,3]:=Simpson(a, b, h5);

writeln ('.........');

gotoxy (wherex, wherey-1);

writeln ('Нижче виведено результати обчислень двома методами з 3 кроками ');

writeln;

write ('Крок:');

gotoxy (13, wherey);

write ('h=', h5:2:6);

gotoxy (35, wherey);

write ('h=', h2:2:6);

gotoxy (57, wherey);

writeln ('h=', h1:2:6);

writeln ('Метод');

write ('Сiмпсона:');

gotoxy (13, wherey);

write ('I=', res[1][3]:5:14);

gotoxy (35, wherey);

write ('I=', res[1][2]:5:14);

gotoxy (57, wherey);

writeln ('I=', res[1][1]:5:14);

write ('Чебишева:');

gotoxy (13, wherey);

write ('I=', res[2][3]:5:14);

gotoxy (35, wherey);

write ('I=', res[2][2]:5:14);

gotoxy (57, wherey);

writeln ('I=', res[2][1]:5:14);

write ('Обчислення похибки.....');

if (a=0) and (b=1) and (c=2.1) and (d=6) then

sharp:=-2.07230756449615

else

sharp:=1.1*Chebushev(a, b, 0.0001);

for i:=1 to 2 do

for j:=1 to 3 do

begin

delta[i][j]:=abs(sharp-res[i][j]);

write('....');

end;

writeln;

gotoxy (wherex, wherey-1);

writeln(' ');

writeln ('Нижче виведено похибки обчислень');

writeln;

write ('Крок:');

gotoxy (13, wherey);

write ('h=', h5:2:6);

gotoxy (35, wherey);

write ('h=', h2:2:6);

gotoxy (57, wherey);

writeln ('h=', h1:2:6);

writeln ('Метод');

write ('Сiмпсона:');

gotoxy (13, wherey);

write ('I=', delta[1][3]:5:14);

gotoxy (35, wherey);

write ('I=', delta[1][2]:5:14);

gotoxy (57, wherey);

writeln ('I=', delta[1][1]:5:14);

write ('Чебишева:');

gotoxy (13, wherey);

write ('I=', delta[2][3]:5:14);

gotoxy (35, wherey);

write ('I=', delta[2][2]:5:14);

gotoxy (57, wherey);

writeln ('I=', delta[2][1]:5:14);

writeln;

writeln ('Для перезавантаження програми натиснiть клавiшу R');

writeln ('Для виходу натиснiть будь-яку клавiшу');

ch:=readkey;

if ch='r' then goto lbl1;

END.