В заданиях 3-5 проверять правильность вычисления переводом исходных данных и результатов в двоичную систему счисления. В задании 1д получить пять знаков после запятой в двоичном представлении.
Таблица 1. Наиболее важные системы счисления.
| Двоичная (Основание 2) | Восьмеричная (Основание 8) | Десятичная (Основание 10) | Шестнадцатиричная (Основание 16) | ||
| триады | тетрады | ||||
| 0 1 | 0 1 2 3 4 5 6 7 | 000 001 010 011 100 101 110 111 | 0 1 2 3 4 5 6 7 8 9 | 0 1 2 3 4 5 6 7 8 9 A B C D E F | 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 |
Перевод целых десятичных чисел в недесятичную систему счисления осуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная с последнего.
Пример.
а) Перевести 18110![]() "8" с.с.
"8" с.с.
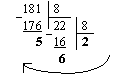
Результат: 18110 = 2658
б) Перевести 62210![]() "16" с.с.
"16" с.с.
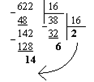
Результат: 62210 = 26E16
Для преобразования в десятичную используют следующую таблицу степеней основания
Преобразование дробных десятичных чисел:· Вначале переводится целая часть десятичной дроби;
· Затем дробная часть десятичной дроби умножается на основание системы счисления;
· В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в системе счисления;
· Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.
Правила выполнения арифметических действий над двоичными числами задаются таблицами двоичных сложения, вычитания и умножения.
| Таблица двоичного сложения | Таблица двоичного вычитания | Таблица двоичного умножения |
| 0+0=0 0+1=1 1+0=1 1+1=10 | 0-0=0 1-0=1 1-1=0 10-1=1 | 0 |
Сложение в восьмеричной системе

Сложение в шестнадцатиричной системе

Умножение в восьмеричной системе

Умножение в шестнадцатеричной системе

1. Перевести данное число из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления
а)945(10)=1110110001(2)=1661(8)=3B1(16)
| 945 | 2 |
| |||||||||||||||||||
| 944 | 472 | 2 |
| ||||||||||||||||||
| 1 | 472 | 236 | 2 |
| |||||||||||||||||
| 0 | 236 | 118 | 2 |
| |||||||||||||||||
| 0 | 118 | 59 | 2 |
| |||||||||||||||||
| 0 | 58 | 29 | 2 |
| |||||||||||||||||
|
| 1 | 28 | 14 | 2 |
| ||||||||||||||||
| 1 | 14 | 7 | 2 |
| |||||||||||||||||
| 0 | 6 | 3 | 2 |
| |||||||||||||||||
| 1 | 2 | 1 | 2 |
| |||||||||||||||||
| 1 | 0 | 0 |
| ||||||||||||||||||
| 1 | 0 |
| |||||||||||||||||||
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | ||||||||||||
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | ||||||||||||
| 512 | 256 | 128 | 32 | 16 | 1 | 945 | |||||||||||||||
| 945,000 | 8,000 | ||
| 944,000 | 118,000 | 8,000 | |
| 1,000 | 112,000 | 14,000 | 8,000 |
| 6,000 | 8,000 | 1,000 | |
| 6,000 | 1,000 |
| 4096 | 512 | 64 | 8 | 1 |
| 1,000 | 6,000 | 6,000 | 1,000 | |
| 945 | 512 | 384 | 48 | 1 |
| 945,000 | 16,000 | |
| 944,000 | 59,000 | 16,000 |
| 1,000 | 48,000 | 3,000 |
| 11,000 | ||
| B | ||
| 3,000 | 11,000 | 1,000 |
| 4096 | 256 | 16 | 1 |
| 3 | 11 | 1 | |
| 945 | 768 | 176 | 1 |
б)85 (10)=1010101(2)=125(8)= 55(16)
| 85 | 2 | ||||||
| 84 | 42 | 2 | |||||
| 1 | 42 | 21 | 2 | ||||
| 0 | 20 | 10 | 2 | ||||
| 1 | 10 | 5 | 2 | ||||
| 0 | 4 | 2 | 2 | ||||
| 1 | 2 | 1 | 2 | ||||
| 0 | 0 | 0 | |||||
| 1 | 0 |
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | ||||
| 64 | 16 | 4 | 1 | 85 |
| 85,000 | 8,000 |
| |||||
| 80,000 | 10,000 | 8,000 |
| ||||
| 5,000 | 8,000 | 1,000 |
| ||||
| 2,000 |
| ||||||
| 4096 | 512 | 64 | 8 | 1 | |||
| 1,000 | 2,000 | 5,000 | |||||
| 85 | 0 | 64 | 16 | 5 | |||
| 85,000 | 16,000 |
| 80,000 | 5,000 |
| 5,000 |
| 4096 | 256 | 16 | 1 |
| 5 | 5 | ||
| 85 | 0 | 80 | 5 |
в)444,125 (10)= 110111100,001(2)=674.1(8)=1BC.2(16)
| 444 | 2 | ||||||||
| 444 | 222 | 2 | |||||||
| 0 | 222 | 111 | 2 | ||||||
| 0 | 110 | 55 | 2 | ||||||
| 1 | 54 | 27 | 2 | ||||||
| 1 | 26 | 13 | 2 | ||||||
| 1 | 12 | 6 | 2 | ||||||
| 1 | 6 | 3 | 2 | ||||||
| 0 | 2 | 1 | 2 | ||||||
| 1 | 0 | 0 | |||||||
| 1 | 0 |
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | ||
| 256 | 128 | 32 | 16 | 8 | 4 | 444 |
| 0,125 | * | 2 | = | 0,250 | 0 |
| 0,250 | * | 2 | = | 0,500 | 0 |
| 0,500 | * | 2 | = | 1,000 | 1 |
| 444,000 | 8,000 |
| |||||||||
| 440,000 | 55,000 | 8,000 |
| ||||||||
| 4,000 | 48,000 | 6,000 |
| ||||||||
| 7,000 |
| ||||||||||
| 4096 | 512 | 64 | 8 | 1 | , | 0,125 | 0,01563 | 0,00195 | |||
| 6,000 | 7,000 | 4,000 | 1 | ||||||||
| 444 | 0 | 384 | 56 | 4 | 0,125 | 0,125 | |||||
| 444,000 | 16,000 | |
| 432,000 | 27,000 | 16,000 |
| 12,000 | 16,000 | 1,000 |
| 11,000 |
| 0,125 | * | 16 | = | 2,000 |
| 4096 | 256 | 16 | 1 | , | 0,0625 |
| 1 | 11 | 12 | 2 | ||
| 444 | 256 | 176 | 12 | 0,125 |
г)989,375 (10)= 111 10111 01 ,011(2)=1735.3(8)=3DD.6(16)
| 989 | 2 | ||||||||||
| 988 | 494 | 2 | |||||||||
| 1 | 494 | 247 | 2 | ||||||||
| 0 | 246 | 123 | 2 | ||||||||
| 1 | 122 | 61 | 2 | ||||||||
| 1 | 60 | 30 | 2 | ||||||||
|
| 1 | 30 | 15 | 2 | |||||||
| 0 | 14 | 7 | 2 | ||||||||
| 1 | 6 | 3 | 2 | ||||||||
| 1 | 2 | 1 | 2 | ||||||||
| 1 | 0 | 0 | |||||||||
| 1 |
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| |||||||||||||||||||
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| |||||||||||||||||||
| 512 | 256 | 128 | 64 | 16 | 8 | 4 | 1 | 989 |
| ||||||||||||||||||||
| 0,375 | * | 2 |
| 0,750 |
| ||||||||||||||||||||||||
| 0,750 | * | 2 | = | 1,500 |
| ||||||||||||||||||||||||
| 0,500 | * | 2 | = | 1,000 |
| ||||||||||||||||||||||||
| |||||||||||||||||||||||||||||
| 989,000 | 8,000 |
| |||||||||||||||||||||||||||
| 984,000 | 123,000 | 8,000 |
| ||||||||||||||||||||||||||
| 5,000 | 120,000 | 15,000 | 8,000 |
| |||||||||||||||||||||||||
| 3,000 | 8,000 | 1,000 |
| ||||||||||||||||||||||||||
| 7,000 | 1,000 |
| |||||||||||||||||||||||||||
| 4096 | 512 | 64 | 8 | 1 | , | 0,125 | 0,01563 | 0,00195 | |||||||||||||||||||||
| 1,000 | 7,000 | 3,000 | 5,000 | 3 | |||||||||||||||||||||||||
| 989 | 512 | 448 | 24 | 5 | 0,375 | 0,375 | |||||||||||||||||||||||
| 989,3750 | |||||||||||||||||||||||||||||
| 989,000 | 16,000 |
| ||||||
| 976,000 | 61,000 | 16,000 |
| |||||
| 13,000 | 48,000 | 3,000 |
| |||||
| 13,000 |
| |||||||
| 3 | D | D |
| |||||
| 0,375 | * | 16 | = | 6,000 | 6,000 | |||
| 4096 | 256 | 16 | 1 | , | 0,0625 | 0,0039063 | 0,0002441 |
| 3 | 13 | 13 | 6 | ||||
| 989 | 768 | 208 | 13 | 0,375 | 0 | 0,375 | |
| 989,375 |
д)237,73 (10)= 11101101,10111(2)=355.5656(8)=ED.BAE(16)
| 237,0 | 2,0 | ||||||||
| 236,0 | 118,0 | 2,0 | |||||||
| 1,0 | 118,0 | 59,0 | 2,0 | ||||||
| 0,0 | 58,0 | 29,0 | 2,0 | ||||||
| 1,0 | 28,0 | 14,0 | 2,0 | ||||||
| 1,0 | 14,0 | 7,0 | 2,0 | ||||||
|
| 0,0 | 6,0 | 3,0 | 2,0 | |||||
| 1,0 | 2,0 | 1,0 | 2,0 | ||||||
| 1,0 | 0,0 | 0,0 | |||||||
| 1,0 |
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| ||||||||||||||||||||
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| ||||||||||||||||||||||
| 128 | 64 | 32 | 8 | 4 | 1 | 237 |
| |||||||||||||||||||||||
| 0,730 | * | 2 |
| 1,460 |
| |||||||||||||||||||||||||
| 0,460 | * | 2 | = | 0,920 |
| |||||||||||||||||||||||||
| 0,920 | * | 2 | = | 1,840 |
| |||||||||||||||||||||||||
| 0,840 | * | 2 | = | 1,680 |
| |||||||||||||||||||||||||
| 0,680 | * | 2 | = | 1,360 |
| |||||||||||||||||||||||||
| 237,000 | 8,000 |
| ||||||||||||||||||||||||||||
| 232,000 | 29,000 | 8,000 |
| |||||||||||||||||||||||||||
| 5,000 | 24,000 | 3,000 |
| |||||||||||||||||||||||||||
| 5,000 | 3,000 |
| ||||||||||||||||||||||||||||
| 4096 | 512 | 64 | 8 | 1 | , | 0,125 | 0,01563 | 0,00195 | 0,00024 | 3,1E-05 | ||||||||||||||||||||
| 3,000 | 5,000 | 5,000 | 5 | 6 | 5 | 6 | ||||||||||||||||||||||||
| 237 | 0 | 192 | 40 | 5 | 0,625 | 0,09375 | 0,00977 | 0,00146 | 0,72998 | |||||||||||||||||||||
| 237,7300 | ||||||||||||||||||||||||||||||
| 237,000 | 16,000 |
| |||||||||||||
| 224,000 | 14,000 |
| |||||||||||||
| 13,000 |
| ||||||||||||||
| 4096 | 256 | 16 | 1 | , | 0,0625 | 0,0039063 | 0,0002441 | ||||||||
| 14 | 13 | 11 | 10 | 14 | |||||||||||
| 237 | 0 | 224 | 13 | 0,6875 | 0,0390625 | 0,7265625 | |||||||||
| 237,727 | |||||||||||||||
| 0,730 | * | 16 | = | 11,680 | B |
| |||||||||
| 0,680 | * | 16 | = | 10,880 | A |
| |||||||||
| 0,880 | * | 16 | = | 14,080 | E |
| |||||||||
а)110001111(2)=399(10)
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | ||
| 256 | 128 | 8 | 4 | 2 | 1 | 399 |
б)111010001(2)=465(10)
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | ||
| 256 | 128 | 64 | 16 | 1 | 465 |
в)100110101,1001(2)=309,5625(10)
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | ||
| 256 | 32 | 16 | 4 | 1 | 309 |
| 1 | 0 | 0 | 1 | |||||||
| 0,5 | 0,25 | 0,125 | 0,063 | 0,031 | 0,02 | 0,01 | 0,0039 | 0,002 | 0,001 | |
| 0,5625 | 0,5 | 0 | 0 | 0,063 |
г)1000010,01011(2)=66,34375(10)
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | ||||
| 64 | 2 | 66 |
| 0 | 1 | 0 | 1 | 1 | ||||||
| 0,5 | 0,25 | 0,125 | 0,063 | 0,031 | 0,02 | 0,01 | 0,0039 | 0,002 | 0,001 | |
| 0,34375 | 0 | 0,25 | 0 | 0,063 | 0,031 |
д)176,5(8)=126.625(10)
| 4096 | 512 | 64 | 8 | 1 | , | 0,125 | 0,01563 | 0,00195 | 0,00024 | 3,1E-05 |
| 1,000 | 7,000 | 6,000 | 5 | |||||||
| 126 | 0 | 64 | 56 | 6 | 0,625 | 0 | 0 | 0 | 0,625 | |
| 126,6250 |
е)3D2,04(16)=978.016(10)
| 4096 | 256 | 16 | 1 | , | 0,0625 | 0,0039063 | 0,0002441 | |||||||||
| 3 | 13 | 2 | 0 | 4 | ||||||||||||
| 978 | 768 | 208 | 2 | 0 | 0,015625 | 0,015625 | ||||||||||
| 978,016 | ||||||||||||||||
| 978,000 | 16,000 |
| ||||||||||||||
| 976,000 | 61,000 | 16,000 |
| |||||||||||||
| 2,000 | 48,000 | 3,000 |
| |||||||||||||
| 13,000 |
| |||||||||||||||
| 0,016 | * | 16 | = | 0,256 | 0,000 |
| ||||||||||
| 0,256 | * | 16 | = | 4,096 | 4 |
| ||||||||||
3. Сложить все числа
а)1000011101(2)+101000010(2)=541(10)+322(10)=1101011111 (2) =863(10)
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | ||
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | ||
| 512 | 0 | 0 | 0 | 0 | 16 | 8 | 4 | 0 | 1 | 541 | |
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | ||
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | |||
| 0 | 256 | 0 | 64 | 0 | 0 | 0 | 0 | 2 | 0 | 322 | |
| 863 | |||||||||||
| + | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | |||
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | ||
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | ||
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | ||
| 512 | 256 | 0 | 64 | 0 | 16 | 8 | 4 | 2 | 1 | 863 |
б)100000001(2)+1000101001(2)=257(10)+553(10)= 1100101010 (2) =810(10)
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | ||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |||
| 0 | 256 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 257 | |
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | ||
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | ||
| 512 | 0 | 0 | 0 | 32 | 0 | 8 | 0 | 0 | 1 | 553 | |
| 810 | |||||||||||
| + | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ||
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | ||
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | ||
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | ||
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | ||
| 512 | 256 | 0 | 0 | 32 | 0 | 8 | 0 | 2 | 0 | 810 |
в)101111011,01(2)+1000100,101(2)=379,25(10)+68,625(10)= (2) =447,875(10)
| 0 | 1 | |||||||||||||
| 0,5 | 0,25 | 0,125 | 0,063 | 0,031 | 0,02 | 0,01 | 0,0039 | 0,002 | 0,001 | |||||
| 0,25 | 0 | 0,25 | ||||||||||||
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |||||
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | ||||||
| 0 | 256 | 0 | 64 | 32 | 16 | 8 | 0 | 2 | 1 | 379 | ||||
| 379,25 | ||||||||||||||
| 1 | 0 | 1 | ||||||||||||
| 0,5 | 0,25 | 0,125 | 0,063 | 0,031 | 0,02 | 0,01 | 0,0039 | 0,002 | 0,001 | |||||
| 0,625 | 0,5 | 0 | 0,125 | |||||||||||
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |||||
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | ||||||||
| 0 | 0 | 0 | 64 | 0 | 0 | 0 | 4 | 0 | 0 | 68 | ||||
| 68,625 | ||||||||||||||
| 447,875 | ||||||||||||||
| + | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | , | 0 | 1 | ||
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | , | 1 | 0 | 1 | ||||
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | , | 1 | 1 | 1 | ||
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |||||
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||
| 0 | 256 | 128 | 0 | 32 | 16 | 8 | 4 | 2 | 1 | 447 | ||||
| 1 | 1 | 1 | ||||||||||||
| 0,5 | 0,25 | 0,125 | 0,063 | 0,031 | 0,02 | 0,01 | 0,0039 | 0,002 | 0,001 | |||||
| 0,875 | 0,5 | 0,25 | 0,125 | |||||||||||
г)1532,14(8)+730,16(8)=858.1875(10)+472.2188(10)=1330.41 (10)=2462.32172(8)
| 32768 | 4096 | 512 | 64 | 8 | 1 | , | 0,125 | 0,01563 | 0,00195 | ||
| 1,000 | 5,000 | 3,000 | 2,000 | 1 | 4 | ||||||
| 858 | 0 | 512 | 320 | 24 | 2 | 0,125 | 0,0625 | 0 | 0,1875 | ||
| 858,1875 |
| 32768 | 4096 | 512 | 64 | 8 | 1 | , | 0,125 | 0,01563 | 0,00195 | ||||||||||||||||||
| 7,000 | 3,000 | 0,000 | 1 | 6 | |||||||||||||||||||||||
| 472 | 0 | 0 | 448 | 24 | 0 | 0,125 | 0,09375 | 0 | 0,21875 | ||||||||||||||||||
| 472,2188 | |||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
| + | 1 | 5 | 3 | 2 | , | 1 | 4 |
| ||||||||||||||||||
| 7 | 3 | 0 | , | 1 | 6 |
| ||||||||||||||||||||
| 2 | 4 | 6 | 2 | , | 3 | 2 |
| |||||||||||||||||||
| 4+6=12 5+7=14 |
| |||||||||||||||||||||||||
| 32768 | 4096 | 512 | 64 | 8 | 1 | , | 0,125 | 0,01563 | 0,00195 | 0,00024 | 3,1E-05 | |||||||||||||||
| 2,000 | 4,000 | 6,000 | 2,000 | 3 | 2 | 1 | 7 | 2 | ||||||||||||||||||
| 1330 | 0 | 1024 | 256 | 48 | 2 | 0,375 | 0,03125 | 0,00195 | 0,00171 | 6,1E-05 | ||||||||||||||||
| 1330,4100 | ||||||||||||||||||||||||||
д) BB,4(16)+2F0,6(16)= 187,25(10)+752.375(10)=939.625(10)=
| 4096 | 256 | 16 | 1 | , | 0,0625 | 0,0039063 | 0,0002441 |
| 11 | 11 | 4 | |||||
| 187 | 0 | 176 | 11 | 0,25 | 0 | 0,25 | |
| 187,250 |
| 4096 | 256 | 16 | 1 | , | 0,0625 | 0,0039063 | 0,0002441 | ||||||
| 2 | 15 | 0 | 6 | ||||||||||
| 752 | 512 | 240 | 0 | 0,375 | 0 | 0,375 | |||||||
| 752,375 | |||||||||||||
| + | 2 | F | 0 | , | 6 |
| |||||||
| B | B | , | 4 |
| |||||||||
| 3 | A | B | , | A |
| ||||||||
| 10 | 11 | 10 |
| ||||||||||
F+B=1A
| 4096 | 256 | 16 | 1 | , | 0,0625 | 0,0039063 | 0,0002441 |
| 3 | 10 | 11 | 10 | ||||
| 939 | 768 | 160 | 11 | 0,625 | 0 | 0,625 | |
| 939,625 |
а)1000101110(2)-1111111(2)= 558(10)-127(10)=110101111 (2) =431(10)
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | |
| 512 | 0 | 0 | 0 | 32 | 0 | 8 | 4 | 2 | 0 | 558 |
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||
| 0 | 0 | 0 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | 127 |
| - | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | |||
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | ||
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | |||
| 0 | 256 | 128 | 0 | 32 | 0 | 8 | 4 | 2 | 1 | 431 |
б)1011101000(2)-1001000000(2)=744(10)-576(10)= 10101000 (2) =168(10)
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | |
| 512 | 0 | 128 | 64 | 32 | 0 | 8 | 0 | 0 | 0 | 744 |
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 512 | 0 | 0 | 64 | 0 | 0 | 0 | 0 | 0 | 0 | 576 |
| - | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | ||||
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | ||
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | ||||
| 128 | 0 | 32 | 0 | 8 | 0 | 0 | 0 | 168 |
в)1000101001,1(2)-1111101,1(2)=553.5(10)-125.5(10)= 110101100,0 (2) =428.0(10)
| 1 | ||||||||||||
| 0,5 | 0,25 | 0,125 | 0,063 | 0,031 | 0,02 | 0,01 | 0,0039 | 0,002 | 0,001 | |||
| 0,5 | 0,5 | |||||||||||
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |||
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | |||
| 512 | 0 | 0 | 0 | 32 | 0 | 8 | 0 | 0 | 1 | 553 | ||
| 553,50 | ||||||||||||
| 1 | ||||||||||||
| 0,5 | 0,25 | 0,125 | 0,063 | 0,031 | 0,02 | 0,01 | 0,0039 | 0,002 | 0,001 | |||
| 0,5 | 0,5 | |||||||||||
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |||
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | ||||||
| 0 | 0 | 0 | 64 | 32 | 16 | 8 | 4 | 0 | 1 | 125 | ||
| 125,500 | ||||||||||||
| 428,000 | ||||||||||||
| - | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | , | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | , | 1 | ||||
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | , | 0 | ||
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |||
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | ||||
| 256 | 128 | 0 | 32 | 0 | 8 | 4 | 0 | 0 | 428 | |||
г)1265,2(8)-610,2(8)=693.25(10)-392.25(10)=301.00(10)=455.0(8)
| 32768 | 4096 | 512 | 64 | 8 | 1 | , | 0,125 | 0,01563 | 0,00195 | 0,00024 |
| 1,000 | 2,000 | 6,000 | 5,000 | 2 | ||||||
| 693 | 0 | 512 | 128 | 48 | 5 | 0,25 | 0 | 0 | 0,25 | |
| 693,2500 |
| 32768 | 4096 | 512 | 64 | 8 | 1 | , | 0,125 | 0,01563 | 0,00195 | 0,00024 | |||||||||||
| 6,000 | 1,000 | 0,000 | 2 | ||||||||||||||||||
| 392 | 0 | 0 | 384 | 8 | 0 | 0,25 | 0 | 0 | 0,25 | ||||||||||||
| 392,2500 | |||||||||||||||||||||
| |||||||||||||||||||||
| - | 1 | 2 | 6 | 5 | , | 2 |
| ||||||||||||||
| 6 | 1 | 0 | , | 2 |
| ||||||||||||||||
| 4 | 5 | 5 | , | 0 |
| ||||||||||||||||
| 8+2-6=4 |
| ||||||||||||||||||||
| 32768 | 4096 | 512 | 64 | 8 | 1 | , | 0,125 | 0,01563 | 0,00195 | 0,00024 |
| ||||||||||
| 4,000 | 5,000 | 5,000 | 2 |
| |||||||||||||||||
| 301 | 0 | 0 | 256 | 40 | 5 | 0,25 | 0 | 0 | 0,25 |
| |||||||||||
| 301,2500 |
| ||||||||||||||||||||
д) 409,D(16)-270,4(16)=1033.813(10)-624.25(10)= 409.563(10)=199.9(16)
| 4096 | 256 | 16 | 1 | , | 0,0625 | 0,0039063 | 0,0002441 |
| 4 | 0 | 9 | 13 | ||||
| 1033 | 1024 | 0 | 9 | 0,8125 | 0 | 0,8125 | |
| 1033,813 |
| 4096 | 256 | 16 | 1 | , | 0,0625 | 0,003906 | 0,000244 | 1,53E-05 |
| 2 | 7 | 0 | 4 | |||||
| 0 | 512 | 112 | 0 | 0,25 | 0 | 0 | 0 | |
| 624 | 624,2500 | 0,25 |
| - | 4 | 0 | 9 | , | D |
| |||||||
| 2 | 7 | 0 | , | 4 |
| ||||||||
| 1 | 9 | 9 | , | 9 |
| ||||||||
| 13-4=9 7+9=10→10-7=9 3-2=1 |
| ||||||||||||
| 4096 | 256 | 16 | 1 | , | 0,0625 | 0,0039063 | 0,0002441 | ||||||
| 1 | 9 | 9 | 9 | ||||||||||
| 409 | 256 | 144 | 9 | 0,5625 | 0 | 0,5625 | |||||||
| 409,563 | |||||||||||||
5. Выполнить умножение
а)111010(2)=*1100000(2)=58(10)*96(10)= 1010111000000(2) =5568 (10)
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 1 | 1 | 1 | 0 | 1 | 0 | |||||
| 32 | 16 | 8 | 0 | 2 | 0 | 58 |
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | ||||
| 64 | 32 | 0 | 0 | 0 | 0 | 0 | 96 |
| * | 1 | 1 | 0 | 0 | 0 | 0 | 0 | |||||
| 1 | 1 | 1 | 0 | 1 | 0 | |||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | ||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | ||||||
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | ||||||
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | ||||||
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4096 | 2048 | 1024 | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4096 | 0 | 1024 | 0 | 256 | 128 | 64 | 0 | 0 | 0 | 0 | 0 | 0 | 5568 |
б)1005.5(8)*63.3(8)= 517,6250(10)*51,3750(10)=26592.98(10)= 63740.7656(8)
| 32768 | 4096 | 512 | 64 | 8 | 1 | , | 0,125 | 0,01563 | 0,00195 | 0,00024 |
| 1,000 | 0,000 | 0,000 | 5,000 | 5 | ||||||
| 517 | 0 | 512 | 0 | 0 | 5 | 0,625 | 0 | 0 | 0,625 | |
| 517,6250 |
| 32768 | 4096 | 512 | 64 | 8 | 1 | , | 0,125 | 0,01563 | 0,00195 | 0,00024 |
| 6,000 | 3,000 | 3 | ||||||||
| 51 | 0 | 0 | 0 | 48 | 3 | 0,375 | 0 | 0 | 0,375 | |
| 51,3750 |
| 32768 | 4096 | 512 | 64 | 8 | 1 | , | 0,125 | 0,015625 | 0,0019531 | 0,0002441 | ||||||||
| 6,000 | 3,000 | 7,000 | 4,000 | 0,000 | 7 | 6 | 5 | 6 | ||||||||||
| 26592 | 24576 | 1536 | 448 | 32 | 0 | 0,875 | 0,09375 | 0,0097656 | 0,9785156 | |||||||||
| 26592,9785 | ||||||||||||||||||
|
| |||||||||||||||||
| * | 1 | 0 | 0, | 5 | 5 |
| |||||||||||
| 6, | 3 | 3 |
| ||||||||||||||
| 3 | 0 | 2 | 0 | 7 |
| ||||||||||||
| 3 | 0 | 2 | 0 | 7 |
| ||||||||||||
| 6 | 0 | 4 | 2 | 6 |
| ||||||||||||
| 6 | 3 | 7 | 4 | 0, | 7 | 7 |
| ||||||||||
3*5=17
3*5+1=17+1=18→(2)0
3*0+2=2
3*0=0
3*1=3
2+6=0
6*5=36
6*5+6=(4)2
6*0+4=4
6*0=0
6*1=6
в)4A,3(16)*F,6(16)= 74.188(10)*15.375(10)=1140.64(10)=474.A2(16)
| 4096 | 256 | 16 | 1 | , | 0,0625 | 0,0039063 | 0,0002441 |
| 4 | 10 | 3 | |||||
| 74 | 0 | 64 | 10 | 0,1875 | 0 | 0,1875 | |
| 74,188 |
| 4096 | 256 | 16 | 1 | , | 0,0625 | 0,0039063 | 0,0002441 | |||||
| 15 | 6 | |||||||||||
| 15 | 0 | 0 | 15 | 0,375 | 0 | 0,375 | ||||||
| 15,375 | ||||||||||||
| * | 4 | A, | 3 |
| ||||||||
| F, | 6 |
| ||||||||||
| 1 | B | D | 2 |
| ||||||||
| 4 | 5 | 8 | D |
| ||||||||
| 4 | 7 | 4, | A | 2 |
| |||||||
6*3=18=1*16+2
6*A=60+1=61=3*16+13→D
6*4=24+3=27=1*16+11→B
F*3=15*3=45=2*16+13→D
F*A=15*10=150+2=9*16+8
F*4=15*4=60+9=69=4*16+5
2+0=2
13+13=26=1*16+10→A
11+8=19+1=20=1*16+4
1+5+1=7
4
| 4096 | 256 | 16 | 1 | , | 0,0625 | 0,0039063 | 0,0002441 |
| 4 | 7 | 4 | 10 | 2 | |||
| 1140 | 1024 | 112 | 4 | 0,625 | 0,0078125 | 0,6328125 | |
| 1140,633 |
Список литературы
1) Пономарёв В.С., Красников В.В. Методические указания по теме: "Арифметические основы ЭВМ":http://static.dstu.edu.ru/informatics/mtdss/part1.html
2) Википедия: http://ru.wikipedia.org/wiki/Двоичная_система_счисления
3) Шауцукова Л.З. Информатика 10 - 11. — М.: Просвещение, 2000 г.: http://www.rus-edu.bg/edu/online/inf/bookinf/theory/chapter4/1_4_10.html
4) Системы счисления Анжелиной Латышевой : http://logika.weebly.com/10571083108610781077108510801077-1074-107410861089110010841077108810801095108510861081-1089108010891090107710841077.html
Похожие работы
... заключается в том, что она чувствительнак знаку числа и по умолчанию при переводе в двоичную систему счисления использует дополнительный "до 1" код, что избавляет нас от написания дополнительной функции перевода. BaseToInt Данная функция реализует алгоритм преобразования числа Base- системы счисления в десятичную по следующей формуле: x = anPn + an-1Pn-1 + ... + a1P1 + a0P0 + ...
... и дробных разрядов. Так, например, сокращенной записи числа 737.25 соответствует его значение, вычисленное согласно равенству (1. 1): 737.25 =7 · 102 + 3 · 101 + 7 · 100 + 2 · 10-1 + 5 · 10-1. В двоичной системе счисления для представления чисел используются две цифры: 0 и 1. Действуя согласно с (1.1), значение двоичного числа, например, 11110010. 0110 можно представить в следующем виде: ...
... рождения (год, число, месяц). 4. Подведение итогов. Домашнее задание. Учить записи в тетрадях. Заключение В данной курсовой работе было рассмотрена роль и место элективных курсов в предпрофильном обучении, а также разработан элективный курс не тему «система счисления» в предпрофильном обучении информатике. В первой части работы были выявлены главные особенности предпрофильной п
... умножать на основание новой системы счисления до тех пор, пока в новой дроби не будет нужного количества цифр, которое определяется требуемой точностью представления дроби. Правильная дробь в новой системе счисления записывается из целых частей произведений получающихся при последовательном умножении, причем первая целая часть будет старшей цифрой новой дроби. Рассмотрим в качестве примера ...







0 комментариев