Навигация
Системы счисления и коды
Задание на курсовую работу
1. Системы счисления
2. Перевод числа из одной системы в другую
3. Машинное представление информации
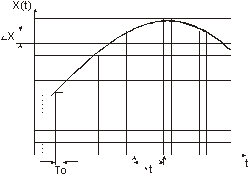
4. Числа с фиксированной точкой
4.1 Прямой код
4.2 Обратный код, инверсный или дополнительный "до 1"
4.3 Дополнительный или дополнительный "до 2" код
5. Схема алгоритма
6. Программная реализация алгоритма
6.1 Общие сведения
6.2 Описание использованных функций и процедур
Библиографический список
Приложение
Рязанская государственная радиотехническая академия
Кафедра САПР вычислительных средств
Задание на курсовую работупо дисциплине " Информатика"
студентке группы 246
Тема: Системы счисления и коды
Срок представления работы к защите: 20 мая 2003г.
Задание:
Разработать программу, которая выполняет следующие действия:
1. Считывает из файла два числа;
2. Переводит эти числа в заданную систему счисления;
3. Выполняет арифметические действия в заданной системе счисления;
4. Переводит полученные результаты в исходную систему счисления и выводит их в файл.
| Форма представления исходных данных и результатов | Система счисления для исходных данных и результатов | Система счисления для выполнения арифметических действий | Выполняемые арифметические действия |
| Целые числа со знаком | шестнадцатеричная | Двоичная, дополнительный код | Сложение вычитание |
Руководитель работы_________________.
Задание выдано 200 г.
Задание принято к исполнению________.
1. Системы счисления
Системой счисления называется совокупность приемов наименования и записи чисел. В любой системе счисления для представления чисел выбираются некоторые символы (их называют цифрами), а остальные числа получаются в результате каких-либо операций над цифрами данной системы счисления. Система называется позиционной, если значение каждой цифры (ее вес) изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.
Число единиц какого-либо разряда, объединяемых в единицу более старшего разряда, называют основанием позиционной системы счисления. Если количество таких цифр равно P, то система счисления называется P-ичной. Основание системы счисления совпадает с количеством цифр, используемых для записи чисел в этой системе счисления.
Запись произвольного числа x в P-ичной позиционной системе счисления основывается на представлении этого числа в виде многочлена
x = anPn + an-1Pn-1 + ... + a1P1 + a0P0 + a-1P-1 + ... + a-mP-m
Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами. При этом нужно только пользоваться теми таблицами сложения и умножения, которые соответствуют данному основанию P системы счисления. В электронных вычислительных машинах применяют позиционные системы счисления с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную и некоторые другие. Наибольшее распространение в вычислительных машинах имеет двоичная система счисления. В этой системе используются только две цифры: 0 (нуль) и 1 (единица). Двоичное изображение числа требует большего (для многоразрядного числа примерно в 3,3 раза) количества разрядов, чем его десятичное представление.
Тем не менее применение двоичной системы позволяет уменьшить общее количество аппаратуры и создаёт большие удобства для проектирования цифровых вычислительных машин, так как для представления в машине разряда двоичного числа может быть использован любой простой элемент, имеющий всего два устойчивых состояния. Такими элементами, например, являются реле, триггерные схемы и т.п. Для представления десятичного разряда потребовалось бы четыре таких элемента. Помимо двоичной системы счисления в вычислительной технике используется также другие системы с недесятичным основанием - восьмеричная и шестнадцатеричная, имеющие основанием соответственно числа 8 и 16. В восьмеричной системе употребляются восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. В шестнадцатеричной системе для изображения чисел употребляется 16 чисел от 0 до 15. При этом, чтобы одну цифру не изображать двумя знаками, приходится вводить специальные обозначения для цифр, больших девяти. Первые десять цифр этой системы обозначают цифрами от 0 до 9, а старшие пять цифр - латинскими буквами: A, B, C, D, E, F.
2. Перевод числа из одной системы в другуюПравила преобразования в восьмеричных и шестнадцатеричных чисел в двоичные исключительно просты, поскольку основания этих систем есть целые степени числа два: 8 = 23, 16 = 24. Для перевода восьмеричного числа в двоичную форму достаточно заменить каждую цифру восьмеричного числа соответствующим трёхразрядным двоичным числом. Таким же образом для перехода от шестнадцатеричной системы к двоичной каждая цифра заменяется соответствующим четырёхразрядным двоичным числом(см таблицу). Например, восьмеричное число 306,4 в двоичной форме записи имеет вид:
![]()
Для перехода от двоичной системы счисления к восьмеричной (или шестнадцатеричной) системе поступают следующим образом: двигаясь от запятой влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем каждую группу из трёх (четырёх) разрядов заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой (см таблицу).
| Десятичное изображение | Двоичное изображение | Восьмеричное изображение | Шестнадцатеричное изображение |
| 0 | 00000 | 0 | 0 |
| 1 | 00001 | 1 | 1 |
| 2 | 00010 | 2 | 2 |
| 3 | 00011 | 3 | 3 |
| 4 | 00100 | 4 | 4 |
| 5 | 00101 | 5 | 5 |
| 6 | 00110 | 6 | 6 |
| 7 | 00111 | 7 | 7 |
| 8 | 01000 | 10 | 8 |
| 9 | 01001 | 11 | 9 |
| 10 | 01010 | 12 | A |
| 11 | 01011 | 13 | B |
| 12 | 01100 | 14 | C |
| 13 | 01101 | 15 | D |
| 14 | 01110 | 16 | E |
| 15 | 01111 | 17 | F |
| 16 | 10000 | 20 | 10 |
При переводе чисел из десятичной системы счисления в систему с основанием P > 1 обычно используют следующий алгоритм:
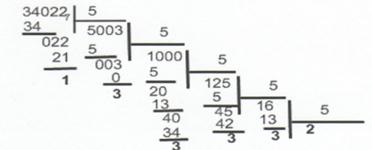
1) если переводится целая часть числа, то она делится на P, после чего запоминается остаток от деления. Полученное частное вновь делится на P, остаток запоминается. Процедура продолжается до тех пор, пока частное не станет равным нулю. Остатки от деления на P выписываются в порядке, обратном их получению;
2) если переводится дробная часть числа, то она умножается на P, после чего целая часть запоминается и отбрасывается. Вновь полученная дробная часть умножается на P и т.д. Процедура продолжается до тех пор, пока дробная часть не станет равной нулю. Целые части выписываются после двоичной запятой в порядке их получения. Результатом может быть либо конечная, либо периодическая двоичная дробь. Поэтому, когда дробь является периодической, приходится обрывать умножение на каком-либо шаге и довольствоваться приближенной записью исходного числа в системе с основанием P.
3. Машинное представление информацииМикропроцессоры обрабатывают упорядоченные двоичные наборы. Минимальной единицей информации является один бит.

Далее следуют - тетрада (4 бита), байт ( byte 8 бит), двойное слово (DoubleWord 16 бит) или длинное (LongWord 16 бит) и учетверенное слова. Младший бит обычно занимает крайнюю правую позицию.
Похожие работы
... и дробных разрядов. Так, например, сокращенной записи числа 737.25 соответствует его значение, вычисленное согласно равенству (1. 1): 737.25 =7 · 102 + 3 · 101 + 7 · 100 + 2 · 10-1 + 5 · 10-1. В двоичной системе счисления для представления чисел используются две цифры: 0 и 1. Действуя согласно с (1.1), значение двоичного числа, например, 11110010. 0110 можно представить в следующем виде: ...
... умножать на основание новой системы счисления до тех пор, пока в новой дроби не будет нужного количества цифр, которое определяется требуемой точностью представления дроби. Правильная дробь в новой системе счисления записывается из целых частей произведений получающихся при последовательном умножении, причем первая целая часть будет старшей цифрой новой дроби. Рассмотрим в качестве примера ...
... 100 10 1001=(9)10 100 11,1=(3,5)10 00 110 00 100 001 100 000 100 10 0 10 00 Таким образом, выполнение арифметических операций в двоичной системе счисления достаточно просто. Особенно просто выполнять операции сложения, вычитания и умножения. Благодоря этому, применение двоичной системы в вычислительных ...
... последовательности 0 и 1. Например целое неотрицательное число А2=Т 111100002 будет храниться в ячейке следующим образом: 1 1 1 1 0 0 0 0 Значит, мы можем записать все числа от 0 до 255 в двоичной системе счисления в 1 ячейке памяти. 2.2 Представление чисел в компьютере Целые числа в компьютере хранятся в ячейках памяти, в этом случае каждому разряду ячейки памяти соответствует ...








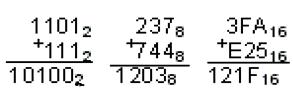
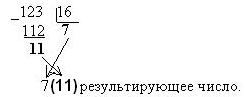
0 комментариев