ДИНАМИЧЕСКИЙ АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА

2. ДИНАМИЧЕСКИЙ АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА

  2.1 Определение скоростей

Для заданной схемы механизма строим 12 положений.

Определяем масштабный коэффициент построения механизма:

  (2.1)

где: - масштабный коэффициент,

 - длина звена,

 - длина звена на чертеже,

Приступаем к построению повёрнутых планов скоростей для каждого положения. Рассмотрим пример построения для положения №5:

 У кривошипа определяем скорость точки А

 (2.2)

где:  - длина звена,

 - угловая скорость кривошипа,

 Для построения вектора скорости точки А определяем масштабный коэффициент

 (2.3)

где:  - скорость точки А,

 - вектор скорости точки А,

 - полюс, выбираемый произвольно

 Для определения скорости точки B запишем систему уравнений:

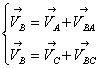 (2.4)

Вектор скорости точки А – V_A известен по величине и по направлению. Вектор скорости точки С – V_C равен нулю, т. к. точка С расположена на неподвижной шарнирной опоре. Вектора скорости V_BA и V_BC неизвестны ни по величине, ни по направлению, но нам известны их линии действия, на пересечении которых мы получим точку b. Соединив, полученную точку с полюсом π найдём длину вектора скорости точки B.

Для определения скорости центра масс 2-го звена S₂ воспользуемся соотношением:

 (2.5)

где: , - расстояния между соответствующими точками на механизме, м

,  - длинны векторов скоростей на плане, мм

 мм

Соединив, точку  и π получим скорость центра масс второго звена.

 Для определения скорости точки D воспользуемся следующим соотношением

 (2.6)

где: , - расстояния между соответствующими точками на механизме, м ,  - длинны векторов скоростей на плане, мм

 мм

Для определения скорости центра масс 3-го звена S₃ воспользуемся соотношением:

 (2.7)

где: , - расстояния между соответствующими точками на механизме, м

,  - длинны векторов скоростей на плане, мм

 мм

т.к. , то

Так как центр массы 4-го звена совпадает точкой D то,

Для определения скорости точки D’ запишем систему уравнений:

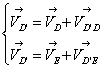 (2.8)

Вектор скорости точки D – V_D известен по величине и по направлению. Вектор скорости точки E – V_E равен нулю, т. к. точка E расположена на неподвижной опоре.

Вектора скорости V_D’D и V_D’E неизвестны ни по величине, ни по направлению, но нам известны их линии действия, на пересечении которых мы получим точку d’. Соединив, полученную точку с полюсом π найдём длину вектора скорости точки D’.

Так как 5-е звено совершает только поступательное движение то, скорости всех точек данного звена одинаковы.

Определим значения угловых скоростей звеньев.

 

Направление  определяем, перенеся вектор ab в точку S₂ – второе звено вращается против часовой стрелки. Аналогично получим, что  направлена по часовой стрелке. Скорости остальных точек определяются аналогичным образом. Все значения сводим в таблицу(2.1).

 Таблица 2.1 – Значения линейных и угловых скоростей.

N положения	VB,	VS2,	VD=VS4,	VS3,	VD’=VS5,	VAB,	,	,
1	0	2,994	0	0	0	4,71	15,596	0
2	2,734	2,933	4,614	1,452	3,367	5,959	19,731	17,089
3	5,335	4,351	9,002	2,834	7,958	4,891	16,194	33,341
4	4,94	4,781	8,337	2,624	8,241	0,767	2,54	30,877
5	3,572	4,113	6,029	1,898	5,989	2,816	9,326	22,328
6	2,166	3,265	3,655	1,151	3,498	4,716	17,177	13,537
7	0	2,994	0	0	0	4,71	15,596	0
8	1,543	3,445	2,604	0,82	2,443	3,659	12,116	9,645
9	3,547	4,237	5,986	1,884	5,877	1,785	5,911	22,17
10	4,596	4,666	7,756	2,441	7,737	0,343	1,135	28,724
11		4,675	7,851	2,472	7,338	0,751	2,487	29,078
12	3,701	4,262	6,246	1,966	5,044	1,999	6,62	23,133

2.2 Определение приведённого момента инерции звеньев.

 Приведённый момент инерции определяется по формуле:

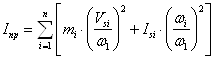 (2.9)

где:  - масса i-го звена рычажного механизма, кг

 - линейная скорость центра масс i-го звена,

 - угловая скорость i-го звена,

 - приведённый момент инерции i-го звена по отношению к центру масс

 (2.10)

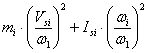 - для звена, совершающего сложное движение

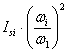 - для звена, совершающего вращательное или колебательное движения

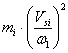 - для звена, совершающего поступательное движение

Запишем формулу для нашего механизма:

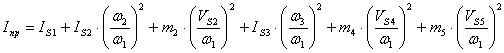 (2.11)

 Для 5-го положения приведём расчёт, а для остальных положений сведём значение в таблицу 2.2

 кг∙м²

 кг∙м²

 кг∙м²

Подставив все известные величины в формулу (2.11) получим:

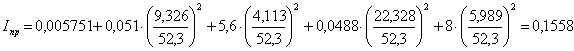 кг∙м²

Таблица 2.2 – Приведённые моменты инерции.

N положения	, кг∙м2	N положения	, кг∙м2
1	0,0286	7	0,0286
2	0,0690	8	0,0519
3	0,2544	9	0,1529
4	0,2683	10	0,2401
5	0,1558	11	0,2232
6	0,0721	12	0,1277

Для построения графика приведённого момента инерции необходимо Рассчитать масштабные коэффициенты.

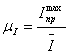,  (2.12)

где:  - масштабный коэффициент по оси

 - максимальное значение , кг∙м²

 - значение  на графике, мм

, (2.13)

где:  - масштабный коэффициент по оси φ

 - принятая длинна одного оборота по оси φ

 

2.3 Определение приведённого момента сопротивления.

 На планах скоростей прикладываем все силы, действующие на механизм, и указываем их плечи. Составляем сумму моментов относительно полюса и решаем уравнение.

Для 1-го положения:

  (2.14)

где:  плечи соответствующих сил, снятые с плана скоростей, мм.

H, H

H

Находим момент привидения:

 (2.15)

где:  - приведённая сила, Н

 - длина соответствующего звена, м

 Н∙м

Для 2-го положения:

  

H

 Н∙м

Для 3-го положения:

  

H

 Н∙м

Для 4-го положения:

  

H

 Н∙м

Для 5-го положения:

  

H

 Н∙м

Для 6-го положения:

  

H

 Н∙м

Для 7-го положения:

  

H

 Н∙м

Для 8-го положения:

  

H

 Н∙м

Для 9-го положения:

  

H

 Н∙м

Для 10-го положения:

  

H

 Н∙м

Для 11-го положения:

  

H

 Н∙м

Для 12-го положения:

  H

 Н∙м

Все значения сводим в таблицу.

Таблица 2.3 – Приведённые моменты сопротивления.

N положения	,	N положения	,
1	-3,09	7	3,104
2	-0,76	8	3,279
3	1,045	9	-87,572
4	0,783	10	-118,594
5	1,139	11	-115,48
6	2,06	12	-82,12

 Определяем масштабный коэффициент построения графика моментов сопротивления:

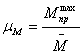,  (2.16)

где:  - масштабный коэффициент по оси

 - максимальное значение ,

 - значение  на графике, мм

 По данным расчёта строится график .

 Путём графического интегрирования графика приведённого момента строится график работ сил сопротивления .

 График работ движущих сил  получаем в виде прямой, соединяющей начало и конец графика работ сил сопротивления.

 Масштабный коэффициент графика работ:

, (2.17)

где: Н – полюсное расстояние для графического интегрирования, мм

 Н=30мм

Момент движущий  является величиной постоянной и определяется графически.

 Путём вычитания ординат графика  из соответствующих ординат  строится график изменения кинетической энергии .

 (2.18)

Таблица 2.4 – Значения ,,

	1	2	3	4	5	6	7	8	9	10	11	12
,	0	-0,39	-0,26	0,08	0,38	0,98	1,78	2,8	0,93	-37,84	-77,52	-114,68
,	0	-7,34	-18,65	-29,96	-41,27	-52,58	-67,2	-75,36	-86,67	-97,98	-109,29	-120,6
,	0	-6,95	-18,39	-30,04	-41,65	-53,56	-68,98	-78,16	-87,6	-60,14	-31,77	-5,92

 По методу Ф. Витенбауэра на основании ранее построенных графиков и  строим диаграмму энергия-масса .

 Определяем углы и  под которыми к диаграмме энергия-масса, проводятся касательные.

 (2.19)

 (2.19)

где:  - коэффициент неравномерности вращения кривошипа.

Вследствие того что, пересечение касательных и оси выходит за приделы формата, то ab определим из геометрии с помощью следующей формулы:

,мм

мм

 Определяем момент инерции маховика

, (2.20)

Маховик устанавливается на валу звена приведения.

Определим основные параметры маховика.

,кг (2,21)

где:  - масса маховика, кг

 - плотность материала,  (материал-Сталь 45)

 - ширина маховика, м

 - диаметр маховика, м

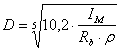,м (2,22)

где:  - коэффициент (0,1÷0,3),

м

м

кг

3. СИЛОВОЙ АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА   3.1 Построение плана скоростей для расчётного положения

Расчётным положением является положение №11. Построение плана скоростей описано в разделе №2. Масштабный коэффициент плана скоростей

 

  3.2 Определение ускорений

Определяем угловое ускорение звена 1.

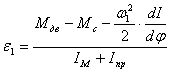, (3.1)

где:  - момент от сил движущих,

 - момент от сил сопротивления,

 - приведённый момент инерции маховика,

 - приведённый момент инерции рычажного механизма для расчётного положения,

 - первая производная от приведённого момента инерции механизма для расчётного положения

, (3.2)

где:  - масштабный коэффициент по оси ,

 - масштабный коэффициент по оси φ,

 - угол между касательной, проведённой к кривой графика  в расчётном положении и осью φ.

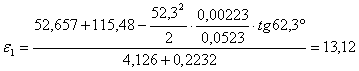
Строим план ускорений для расчётного положения.

Скорость точки А определяем по формуле

, (3.3)

где:  - ускорение точки А,

 - нормальное ускорение точки А относительно точки О,

 - тангенциальное (касательное) ускорение точки А,

Ускорение  найдём по формуле:

, (3.4)

где:  - угловая скорость кривошипа,

 - длина звена ОА, м

Ускорение  найдём по формуле:

, (3.5)

Из произвольно выбранного полюса откладываем вектор длинной 100мм. Найдём масштабный коэффициент плана скоростей.

, (3.6)

Определим длину вектора :

Т.к. <1мм, то на плане ускорений вектор не строим.

Ускорение точки А определим из следующеё формулы:

 Определим ускорение точки B из следующей системы уравнений:

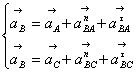, (3.7)

Для определения нормальных ускорений точки В относительно точек А и С

Воспользуемся следующими формулами:

Ускорение точки С равно нулю, т.к. она неподвижна.

Определим длину векторов  и :

Т.к. <1мм, то на плане ускорений вектор не строим.

Ускорение точки В найдём, решив системе (3.7) векторным способом:

Из вершины вектора ускорения точки А () откладываем вектор  (параллелен звену АВ и направлен от В к А), из вершины вектора  проводим прямую перпендикулярную звену АВ (линия действия ); из полюса  откладываем вектор (параллелен звену ВС и направлен от В к С), из вершины вектора  проводим прямую перпендикулярную звену ВС (линия действия ); на пересечении линий действия векторов и  получим точку b, соединив полученную точку с полюсом, получим вектор ускорения точки В. Из плана ускорений определяем вектора тангенциальных ускорений и ускорение точки В:

 Из полученных тангенциальных ускорений найдём угловые ускорения 2-го и 3-го звеньев:

 Ускорение точки D найдём из следующего соотношения:

 (3.8)

где: , - расстояния между соответствующими точками на механизме, м

,  - длинны векторов ускорений на плане, мм

 мм

 Ускорение точки D’ определим из следующей системы уравнений:

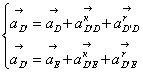, (3.9)

где: ==0, т.к. звенья 4 и 5 не совершают вращательного движения,

линия действия  направлена вертикально,

линия действия  направлена горизонтально.

Решая систему (3.9) получимУскорение точки D’ равно:

 Определим ускорения центров масс звеньев:

Ускорение центра масс 2-го звена  найдём из соотношения (3.10)

 (3.10)

Из плана ускорений мм

мм

мм

Ускорение центра масс 3-го звена  найдём из соотношения (3.11)

 (3.10)

Из плана ускорений мм

мм

мм

Ускорения центров масс 4-го и 5-го звеньев равны ускорениям точек D и D’ соответственно:

 Значения всех ускорений сведём в таблицу:

Таблица З.1 – Ускорения звеньев.

Ускорение точек механизма	Значение,	Ускорение центров масс	Значение,	Угловые ускорения	Значение,
				---	---
		---	---	---	---
		---	---	---	---
		---	---	---	---
		---	---	---	---
		---	---	---	---
		---	---	---	---

 
3.3 Определение сил и моментов инерции звеньев

 Силы инерции определяем по формуле:

 (3.11)

где:  - масса i-го звена, кг ;

 - ускорение центра масс i-го звена,

 

 Определяем моменты инерции звеньев:

 (3.12)

где:  - момент инерции i-го звена,  

 - момент инерции i-го звена относительно центра масс,

 - угловая скорость i-го звена,

Рассчитаем силу тяжести каждого звена:

  3.4 Определение реакций в кинематических парах и уравновешивающей силы методом планов

Рассмотрим группу Асура 5-0: Силаи найдем из следующего уравнения:

Масштабный коэффициент сил:

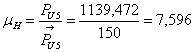
где - алгебраическое значение силы, Н

длина вектора силы на плане, .

Определим длины векторов: ,

Из плана сил определяем значения неизвестных сил:

Таблица 3.2 – Силы и вектора сил 4-го звена.

	78,4	1139,472	800	78,4	339,472
	10,321	150	105,318	10,321	44,691

Рассмотрим звено №4 (ползун):

Так как силы и равны нулю, то на ползун действует только две силы, которые расположены на одной прямой и противоположны по направлению.

Рассмотрим группу Асура 2-3:

Найдём тангенциальные реакции из следующих уравнений:

 (3.13)

 (3.14)

Из уравнения (3.13) получим

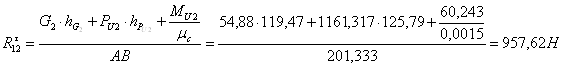
Из уравнения (3.14) получим

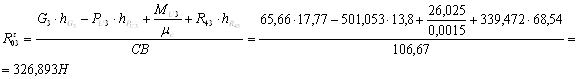
С помощью плана сил определим неизвестные реакции  и :

Найдём масштабный коэффициент

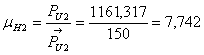
Из плана сил определяем значения неизвестных сил:

Реакцию  определяем из следующего векторного уравнения

Таблица 3.3 – Силы и вектора сил 2-го и 3-го звеньев.

	954,968	957,62	1352,403	1161,317	54,88	339,472	65,66	501,053	326,893	901,331
	123,349	123,691	174,684	150	7,089	43,848	8,481	64,719	42,223	116,421

Рассмотрим начальный механизм.

Определим уравновешивающую силу

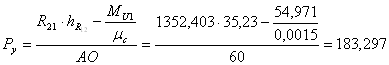
Уравновешивающий момент равен

Реакцию  определяем графически

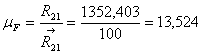
Из плана сил находим