Навигация
Построение графика частот вращения
3.4 Построение графика частот вращения
График частот вращения (рисунок 11) отражает частоты вращения всех валов привода, включая валы одиночных передач, необходимых для его компоновки. Построение начинают с цепи редукции, обеспечивающей снижение частоты вращения электродвигателя nэд. до nmin на шпинделе. Для дальнейшего построения используется структурная сетка.
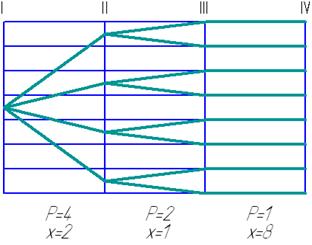
Рисунок 10 – Структурная сетка
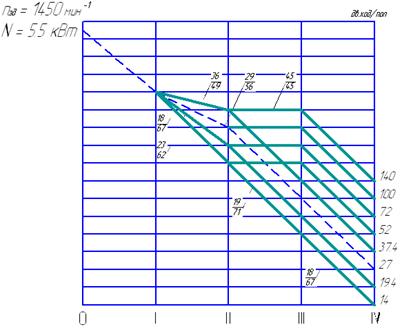
Рисунок 11 – График числа двойных ходов ползуна
3.5 Определение передаточных отношений в группах передач
Для определения передаточных отношений используются построенные графики частот вращения.
Передаточное отношение передачи u, определяется выражением:
u = jk, (3.17)
где k – число интервалов между горизонталями, перекрытых лучами, соединяющими отметки частот вращения на соседних валах.
3.6 Определение чисел зубьев передач
При определении чисел зубьев исходят из постоянства межосевого расстояния и числа зубьев, определяют по следующим формулам:
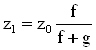 , (3.18)
, (3.18)
 , (3.19)
, (3.19)
![]() , (3.20)
, (3.20)
![]() (3.21)
(3.21)
где z1 и z2 – числа зубьев ведущего и ведомого колес;
z0 – сума чисел зубьев сопряженных колес;
f – числитель передаточного отношения;
g – знаменатель передаточного отношения;
K – наименьшее кратное сумм (f + g);
Е – целое число;
zmin= 18 – минимальное число зубьев.
В соответствии с полученными числами зубьев передач, вычерчивается вариант кинематической структуры (рисунок 12).
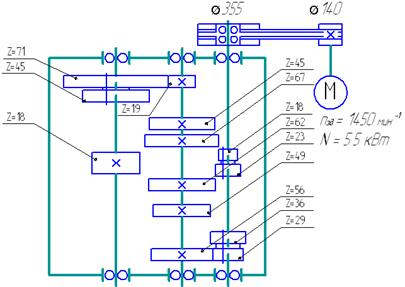
Рисунок 12 – Кинематическая структура коробки скоростей
3.7 Определение крутящих моментов на валах коробки скоростейКрутящие моменты на валах Т, Н·м, могут быть найдены по формуле:
![]() (3.22)
(3.22)
где Рэд. – мощность на валу двигателя, кВт;
h – КПД участка кинематической цепи от двигателя до рассчитываемого вала;
n – расчетная частота вращения вала, об/мин.
Кинематический расчет коробки скоростей выполнен с использованием программы «SIRIUS 2». Результаты расчета находятся в приложении А.
3.8 Расчет прямозубой эвольвентной передачи
Определение модуля зубчатой передачи расчетом на контактную выносливость зубьев
Для прямозубой цилиндрической передачи модуль mн, мм, определяется по формуле:
 (3.23)
(3.23)
где Kd – вспомогательный коэффициент; для прямозубых передач Kd = 770;
z1 – число зубьев шестерни;
T1 – вращающий момент на шестерне, Н×м;
u – передаточное отношение передачи;
sНР – допускаемое контактное напряжение, МПа;
KHb – коэффициент, учитывающий распределение нагрузки по ширине венца;
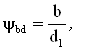 (3.24)
(3.24)
где b – рабочая ширина венца зубчатой передачи;
d1 – делительный диаметр шестерни.
Определение модуля зубчатой передачи расчетом на выносливость зубьев при изгибеДля прямозубой цилиндрической передачи модуль mF, мм, определяется по формуле:
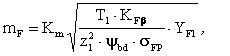 (3.25)
(3.25)
где Km – вспомогательный коэффициент; для прямозубых передач Km = 14;
KFb – коэффициент, учитывающий распределение нагрузки по ширине венца при изгибе;
sFP – допускаемое изгибное напряжение, МПа;
YF1 – коэффициент учитывающий форму зубьев шестерни.
Определение стандартного модуля зубчатой передачиИз полученных расчетных значений mH и mF выбирается наибольшее значение и округляется в сторону увеличения до стандартного модуля по ГОСТ 9563 – 60. При этом должно выполняться следующее условие:
m1 £ m2 £ … £ mk, (3.26)
где m1 – модуль зубчатых передач группы, расположенной первой от электродвигателя;
mk – модуль зубчатых передач группы, расположенной последней от электродвигателя.
Определение межосевого расстояния зубчатой передачиДля прямозубой цилиндрической передачи межосевое расстояние А, мм, определяется по формуле:
![]() (3.27)
(3.27)
где m – стандартный модуль передачи, мм;
z2 – число зубьев зубчатого колеса, сопряженного с шестерней.
При определении межосевых расстояний по группам передач должно выполняться следующее условие:
Aw1 £ Aw2 £ … £ Awk, (3.28)
где Aw1 – межосевое расстояние передач группы, расположенной первой от электродвигателя;
Awk – межосевое расстояние передач группы, расположенной последней от электродвигателя.
Расчет прямозубой эвольвентной передачи выполнен с использованием программы «SIRIUS 2». Результаты расчета находятся в приложении Б.
0 комментариев