Навигация
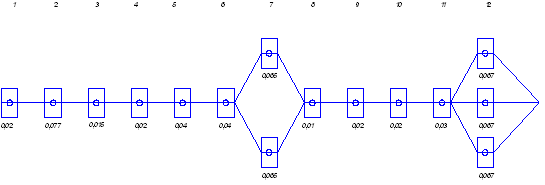
2. Симплекс-метод
Решить систему уравнений:
Найти значения, при которых целевая функция
.
Приведем все знаки к одному направлению:
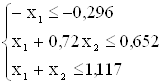
Для перехода от системы неравенств, вводим в систему уравнений единичную матрицу. Расширенная форма записи:
;
.
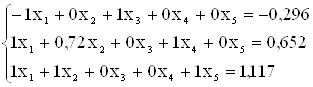Находим расширенную матрицу, матрицу свободных членов и матрицу коэффициентов при базисных переменных:
.
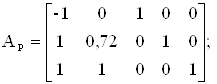
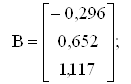
Выбираем исходный базис. Запишем матрицу коэффициентов при базисных переменных:
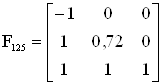
Найдем определитель матрицы коэффициентов при базисных переменных:
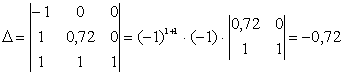
Находим союзную матрицу:
|
|
|
|
|
|
|
|
|
|
|
|
; 
; 
; 
; 
; 
; 
; 
; 
. 
Находим транспонированную матрицу:
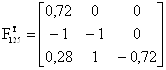
Находим обратную матрицу:
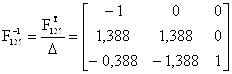
Находим решение исходного базиса:
;
.
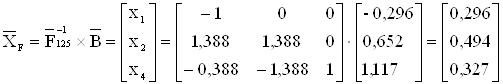Базисное решение является допустимым, т.к все его значения положительные.
Вычислим симплекс-разности для всех переменных, не вошедших в базис:
;
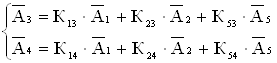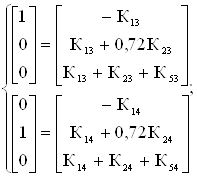
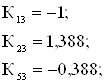
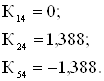
Симплекс разности отрицательны, следовательно, найдено оптимальное решение: 
Вывод: результаты, полученные графическим и симплекс-методом совпали, значит задача решена правильно.
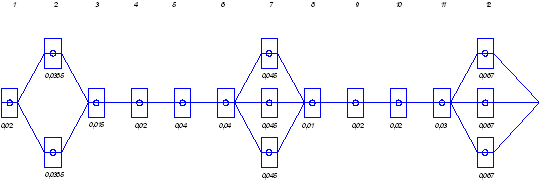
3. Симплекс-таблицы. Решить систему уравнений:
Найти значения, при которых целевая функция
.
Приведем все знаки к одному направлению:
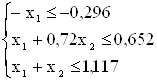
Для перехода от системы неравенств, вводим в систему уравнений единичную матрицу. Расширенная форма записи:
; 
.
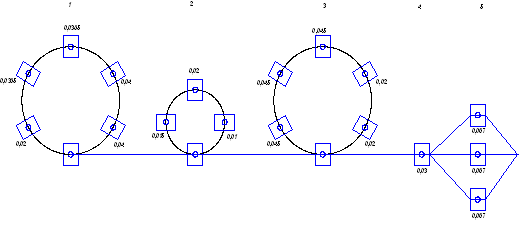
Приведем систему уравнений к виду, где выделены базисные переменные:
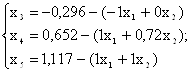
По последней записи системы уравнений и целевой функции построим таблицу 1.
После нахождения разрешающего элемента в таблице 1, переходим к заполнению таблицы 2. После построения таблицы 2 в последней строке имеется положительный элемент, значит оптимальное решение не найдено.
Определяем разрешающий элемент в таблице 2 и переходим к заполнению таблицы 3.
Таблица 3.
| Таблица 1 | Таблица 2 | Таблица 3 | |||||||||||
| СН БН | СЧ | х1 | х2 | СН БН | СЧ | x4 | x2 | СН БН | СЧ | x4 | x3 | ||
| x3 | -0,296 | -1 | 1 | x3 | 0,356 | 1 | 0,72 |
| x2 | 0,494 | 1,388 | 1,388 | |
| x4 | 0,652 | 1 | 0,72 |
| x1 | 0,652 | 1 | 0,72 | x1 | 0,296 | 0 | -1 | |
| x5 | 1,117 | 1 | 1 | x5 | 0,465 | -1 | 0,28 | x5 | 0,327 | -1,388 | -0,388 | ||
| zmin | -0,135 | 1 | 1 | zmin | -0,787 | -1 | 0,28 | zmin | -0,925 | -1,388 | -0,388 | ||
|
|
| ||||||||||||
В таблице 3 все элементы последней строки отрицательны, значит оптимальное решение найдено:
.
Вывод: результаты, полученные графическим методом и методом симплекс-таблиц совпали, значит, задача решена правильно.
Похожие работы
... 500 - 100 0,2 шлифовальная Шлифовать пов. 6 Круг СМ1 0,4 - - 300 6,0 14 24 1,6 Шлифовать торец 14 Круг СМ1 0,4 - - 300 6,0 18 109 1,6 В данной работе предлагается разработка автоматической линии для осуществления той части техпроцесса, которая связана с обработкой отверстий и фрезерованием канавок. Таким образом, для данной линии не учитываются токарные и шлифовальные ...
... устройства можно быстро открыть и закрыть зону резания, пользуясь рукояткой 5. Рассеиванию стружки вдоль стола препятствуют боковые неподвижные щиты 2. Рис. 5. Ограждение зоны резания вертикально-фрезерного станка 4. Ограждения и защитные устройства Все вращающиеся части оборудования должны быть закрыты глухими кожухами, плотно прикрепленными к раме или другой части стенда. Кожухи на ...
... колесо-рейка). Приводы должны обеспечивать широкий диапазон режимов обработки, максимальную производительность, высокую точность позиционирования исполнительных органов. Анализируя существующую гамму вертикально фрезерных станков, приходим к выводу, что целесообразно применить традиционную схему цепи подач со ступенчатым регулированием режимов обработки. Вращение от электродвигателя передаётся ...
... зданий и сооружений + текущий ремонт и содержание оборудования: 20293,65 грн. + 48412,7 грн. = 68706,35 грн. 3. Расчет экономической эффективности технического решения Техническое решение курсовой работы – замена в токарных станках системы управления на: а) ТП-Д и б) ТПЧ. В результате этого решения норма, зона обслуживания этих станков не изменяется, по этому штат рабочих не меняется ...
0 комментариев