Границы применимости линейного закона фильтрации

3.3 Границы применимости линейного закона фильтрации

Так же как и для гранулярных (пористых) сред, при больших скоростях фильтрации линейный закон фильтрации может нарушаться из-за появления значительных по величине сил инерции. Как показали исследования Г. М. Ломизе, для движения воды в щелях различного вида характерны числа Re, значительно превы шающие величины этого параметра для пористых сред: так, для щелей с гладкими стенками верхний предел применимости линейного закона оценивается числами Re_кр = 600, а нижний —Re_кр = 500).

Ф. И. Котяхов указывал, что для трещиноватых пород за счет изменения относительной шероховатости трещин и их различного раскрытия (от 71 мк до 12,96 мк в опытах Ф. И. Котяхова) нарушение линейного закона происходит при значениях Re соответственно от 90 до 0,40. Исследования Е. С. Ромма подтвердили, что для щелей с гладкими стенками критическое число Рейнольдса равно 500. Им было также установлено, что если величина относительной шероховатости меньше 0,065, то ее роль в процессах фильтрации может не учитываться.

Параметр Re для трещиноватой среды можно ввести на основании следующих простых рассуждении.

(2.17)

Безразмерный параметр Re для щели любой формы определяется выражением:
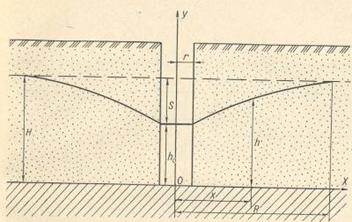
где u — средняя скорость потока в м/сек; v — кинематическая вязкость в м/сек; R — гидравлический радиус (отношение площади «живого» сечения потока к «смоченному» периметру) в м. Для трещин прямоугольного сечения:

(2.18)

где а — ширина трещин.

Приближенное выражение для R получено на основании того, что обычно d < а и величиной d в знаменателе по сравнению с а можно пренебречь. Заметим, что d — среднее раскрытие трещин в породе.

(2.19)

Таким образом,

и учитывая, что

(2.20)

то выражение для числа Рейнольдса в трещиноватой фильтрирующей среде может быть представлено в окончательной форме:
Отметим, что согласно сказанному, за нижнюю границу нарушения линейного закона фильтрации в трещиноватом пласте следует принять Rе_др = 0,4. Понятно, что если линейный закон фильтрации не действителен для трещиноватых пластов, следует использовать нелинейные законы.

(2.21)

Аналитически нелинейные законы выражаются в виде одночленных и двучленных формул. Одночленная формула предполагает следующую запись:
где п изменяется от 1 до 1,75 (по данным проф. Г. М. Ломизе).

(2.22)

Значение постоянной С_т можно получить методами теории подобия. Аналогичными рассуждениями получаем, что:

(2.23)

 где

где

(2.24)

На основании (2.19) уравнение (2.18) можно записать в виде:

где n = 1 — 1,75.

При n = 1,75 имеем турбулентный режим. Если линейный закон нарушается, используется двучленная формула, учитывающая возрастающую роль сил инерции в связи с увеличением скоростей движения жидкостей и газов:

(2.25)

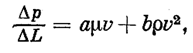
где a, b — некоторые постоянные.

Б. Ф. Степочкиным на основе обработки обширного эксперимен тального материала (по результатам опытных данных и заимствован ного из различных литературных источников) для большого диапа зона размеров (от нескольких микрон до 75 мм) твердых частиц раз нообразной формы (слагающих продуктивные пласты) и интервала чисел Re от 10^-6 до 10³, получена двучленная формула:

(2.26)

где d — диаметр зерен, составляющих среду