Навигация
Вывод уравнения Лапласа. Плоские задачи теории фильтрации
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Курсовая работа
По курсу «Подземная гидромеханика»
Тема: «Вывод уравнения Лапласа. Плоские задачи теории фильтрации»
2009
Содержание
Введение
1. Дифференциальные уравнения движения сжимаемой и несжимаемой жидкости в пористой среде. Вывод уравнения Лапласа.
2. Плоские задачи теории фильтрации
2.1 Приток к совершенной скважине
2.1.1 Фильтрационный поток от нагнетательной скважины к эксплуатационной
2.1.2 Приток к группе скважин с удаленным контуром питания
2.1.3 Приток к скважине в пласте с прямолинейным контуром питания
2.1.4 Приток к скважине, расположенной вблизи непроницаемой прямолинейной границы
2.1.5 Приток к скважине в пласте с произвольным контуром питания
2.1.6 Приток к бесконечным цепочкам и кольцевым батареям скважин
2.1.6.1 Приток к скважинам кольцевой батареи
2.1.6.2 Приток к прямолинейной батареи скважин
2.1.7 Метод эквивалентных фильтрационных сопротивлений
Вывод
Литература
Введение
Подземная гидромеханика — наука о движении жидкостей, газов и их смесей в пористых и трещиноватых горных породах — теоретическая основа разработки нефтяных и газовых месторождений, одна из профилирующих дисциплин в учебном плане промыслового и геологического факультетов нефтяных вузов.
В основе подземной гидравлики лежит представление о том, что нефть, газ и вода, заключенные в пористой среде, составляют единую гидравлическую систему.
Теоретической основой ПГД является теория фильтрации - наука, описывающая данное движение флюида с позиций механики сплошной среды, т.е. гипотезы сплошности (неразрывности) течения.
Особенностью теории фильтрации нефти и газа в природных пластах является одновременное рассмотрение процессов в областях, характерные размеры которых различаются на порядки: размер пор (до десятков микрометров), диаметр скважин (до десятков сантиметров), толщины пластов (до десятков метров), расстояния между скважинами (сотни метров), протяженность месторождений (до сотен километров).
В данной курсовой работе выводится основное уравнение Лапласа и рассматриваются плоские задачи теории фильтрации, а так же их решение.
1. Дифференциальные уравнения движения сжимаемой и несжимаемой жидкости в пористой среде. Вывод уравнения Лапласа
При выводе дифференциального уравнения движения сжимаемой жидкости исходными уравнениями являются следующие:
закон фильтрации жидкости; в качестве закона фильтрации принимаем линейный закон фильтрации, выражающийся формулами (3.1)
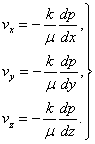 , (3.1)
, (3.1)
уравнение неразрывности (3.2)
![]() , (3.2)
, (3.2)
уравнение состояния. Для капельной сжимаемой жидкости уравнение состояния может быть представлено в виде (3.3)
![]() , (3.3)
, (3.3)
где ![]() - плотность жидкости при атмосферном давлении
- плотность жидкости при атмосферном давлении ![]() .
.
Подставляя в уравнение неразрывности (3.2) вместо проекций скорости фильтрации vx, vy и vz их значения из линейного закона, выражающегося формулой (3.1), получим:
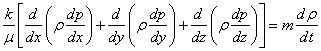 , (3.4)
, (3.4)
уравнения состояния (3.3) имеем:
![]() , (3.5)
, (3.5)
Откуда
![]() ,
,
![]() ,
,
![]() . (3.6)
. (3.6)
Подставляя эти значения частных производных ![]() ,
, ![]() и
и ![]() в уравнение (3.4), получим:
в уравнение (3.4), получим:
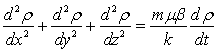
Вводя оператор Лапласа
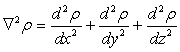
уравнение (3.7) более кратко можно написать в виде
![]() , (3.8)
, (3.8)
Учитывая, что
 , (3.9)
, (3.9)
уравнение (3.7) можно приближенно представить в виде:
 ,(3.10)
,(3.10)
Уравнение (3.7) или приближенное заменяющее его уравнение (3.10) есть искомое дифференциальное уравнение неустановившегося движения сжимаемой жидкости в пористой среде. Упомянутые уравнения имеют вид «уравнения теплопроводности», интегрирование которого при различных начальных и граничных условиях рассматривается в каждом курсе математической физики.
Решение различных задач о неустановившемся движении однородной сжимаемой жидкости в пористой среде, основанное на интегрировании уравнения (3.7) при различных начальных и граничных условиях, дается в книгах В. Н. Щелкачева, И. А. Чарного и М.Маскета. При установившемся движении сжимаемой жидкости 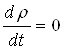 и вместо уравнения (3.7) имеем:
и вместо уравнения (3.7) имеем:
 , (3.11)
, (3.11)
Уравнение (3.11) называется уравнением Лапласа.
При установившейся и неустановившейся фильтрации несжимаемой жидкости плотность жидкости постоянна следовательно, величина, стоящая в правой части уравнения (3.4), равна нулю. Сокращая левую часть этого уравнения на постоянную ![]() и выполнив дифференцирование, получим:
и выполнив дифференцирование, получим:
 , (3.12)
, (3.12)
Таким образом, установившаяся и неустановившаяся фильтрация несжимаемой жидкости описывается уравнением Лапласа (3.12).
Похожие работы
... влияния – RТ и чистой воды – Rwдля некоторого момента времени 3.6. Выводы В нулевом и первом приближениях решена задача о температурном поле, вызванном закачкой радиоактивного раствора в глубокозалегающие пласты. На основании полученного решения установлены расчетные формулы для полей температуры, вызванных энергией распада и различием температур пласта и закачиваемой жидкости. ...
... системам линейных алгебраических уравнений с более чем одной неизвестной; MATLAB решает такие уравнения без вычисле-ния обратной матрицы. Хотя это и не является стандартным математическим обозначением, система MATLAB использует терминологию, связанную с обычным делением в одномерном случае, для описания общего случая решения совместной системы нескольких линейных уравнений. Два символа деления / ...
... Из этой теоремы следует, что класс функций, представимых рядами Фурье, довольно широк. Поэтому ряды Фурье нашли широкое применение в различных отделах математики. Особенно успешно ряды Фурье применяются в математической физике и её приложениях к конкретным задачам механики и физики. Этот вопрос можно решить с помощью теоремы Дирихле. («Краткий курс высшей математики», Шнейдер и др., стр. 181) ...
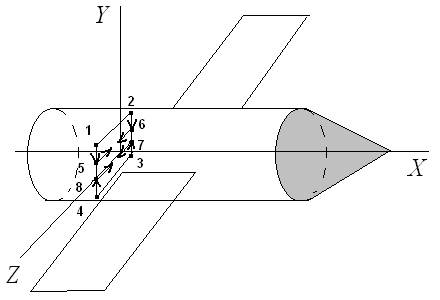
... , может приводить к большим потерям рабочего тела и раскрутке космического аппарата до недопустимых угловых скоростей. Таким образом разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппарата – является актуальной задачей. В настоящей работе решается задача построения алгоритмов контроля и идентификации отказов командных приборов и исполнительных органов. ...



0 комментариев