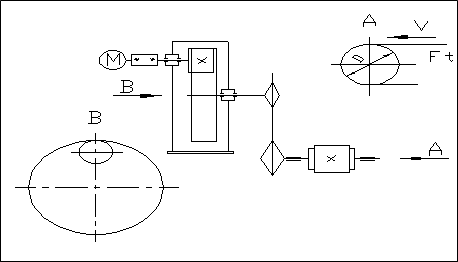
Навигация
3.9 Расчет и подбор шпонок
На I вал (под шкиф):
Подбираем стандартную шпонку под вал диаметром 36 мм.:
l = 28 мм. b = 10 мм, h = 8 мм, t1 = 3.3 мм, t = 5 мм;
lр = 28 – 10 = 28 мм;
![]()
где ![]() - фактические и допускаемые напряжения смятия, МПа;
- фактические и допускаемые напряжения смятия, МПа;
d - диаметр вала, мм;
lр - рабочая длина призматической шпонки, мм. (lр = l - b, где: l - длина шпонки, b - ширина шпонки);
h - стандартная высота шпонки, мм;
t1 - глубина шпоночного паза, мм.
![]()
где ![]() - фактические и допускаемые напряжения среза, МПа,
- фактические и допускаемые напряжения среза, МПа,
b - стандартная ширина шпонки, мм.
На I вал (под колесом 3):
Подбираем стандартную шпонку под вал диаметром 42 мм.:
l = 36 мм, b = 12 мм, h = 8 мм,; t1 = 3,3 мм; t = 5 мм
lр = 36 – 12 = 24 мм;
![]()
![]()
На II вал (под колесом 4):
Подбираем стандартную шпонку под вал диаметром 48 мм.:
l = 40 мм, b = 14 мм, h = 9 мм, t1 = 3.8 мм, t = 5,5 мм;
lр = 40 – 14 = 26 мм;
![]()
![]()
На II вал (под колесом 5):
Подбираем стандартную шпонку под вал диаметром 50 мм.:
l = 40 мм, b = 14 мм, h = 9 мм, t1 = 3.8 мм, t = 5,5 мм;
lр = 40 – 14 = 26 мм;
![]()
![]()
На III вал (под колесом 6):
Подбираем стандартную шпонку под вал диаметром 63 мм.:
l = 45 мм, b = 18 мм, h = 11 мм, t1 = 4,4 мм, t = 7 мм;
lр = 45 – 18 = 27 мм;
![]()
![]()
На III вал (под муфтой):
Подбираем стандартную шпонку под вал диаметром 45 мм.:
l = 45 мм, b = 14 мм, h = 9 мм, t1 = 3,3 мм;
lр = 45 – 14 =31 мм;
![]()
![]()
Прочность шпонок на смятие и срез обеспечивается.
Расчет вала на прочность
Материал вала сталь 45:
σВ = 500 МПа;
στ = 280 МПа;
ττ = 150 МПа;
σ-1 = 250 МПа;
τ-1 = 150 МПа;
ψτ = 0;
[σИ]III = 43,5 МПа
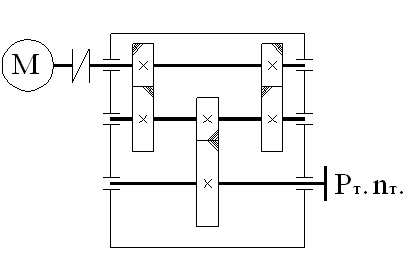
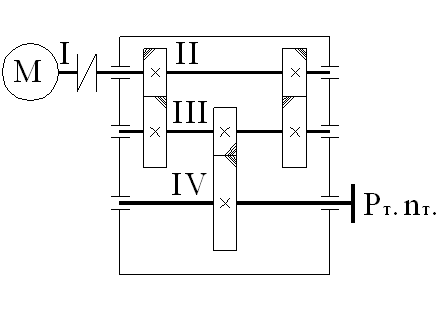
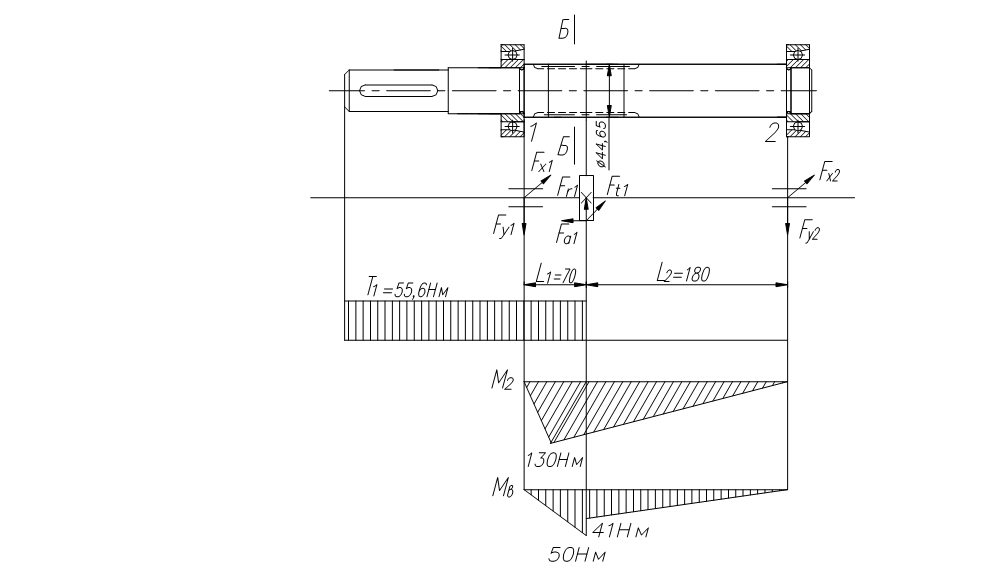
Входной вал:
Силы, действующие на вал, плечи сил Fa:
Fшк = 1267,1 H
Ft1Б = 2 ·М2 / d2 = 2 ·326,345/ 0,209= 3123 H;
Fr1Б = Fr2Б = F t1Б · tgαw/cosβ = 3123· tg21,22/cos20,37 = 1293,5 H;
Fa1Б = F t1Б · tgβ = 3123· tg20,37 = 1160 H;
Fм = (2·М / d)0,2= (2 · 519682 / 45)0,2 = 4619,4H
Ft1Т = 2 ·М2 / d2 = 2 ·524 920/ 202,35= 5188,24 H;
Fr1Т = Fr2Т = F t1Т · tgαw/cosβ = 5188,24 · tg20/cos0 = 1888,4 Н.
Т2 = 180,67 Н∙м;
Т4 = 326,345 Н∙м;
Т6 = 524,92 Н∙м;


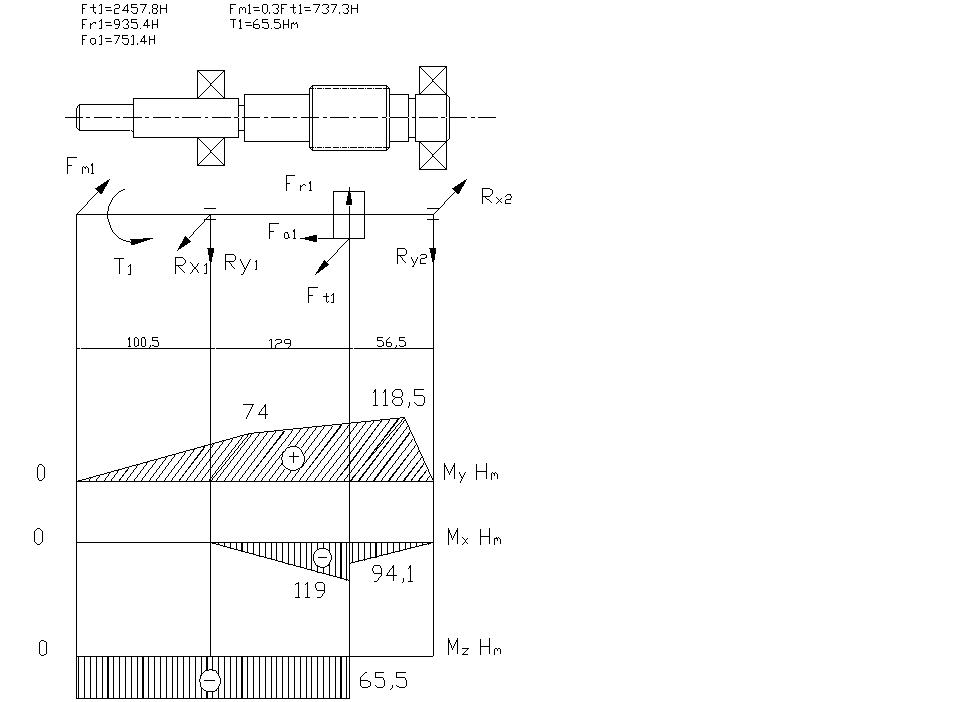
Рассмотрим вал №1:
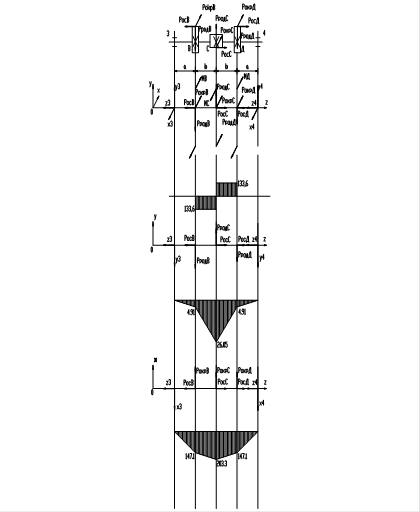
Построение эпюр изгибающих моментов в вертикальной и горизонтальной плоскостях.
Вертикальная плоскость:
Определяем реакции опор:
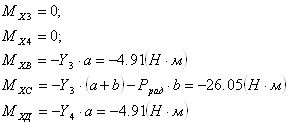
∑М1У = 0, -105Fшк - 65· Fr - Fa·d/2 + 115· R2r = 0,
-105·1267,1 - 65· 1293,5 - 1160·111/2 + 115· R2r = 0,
115· R2r = 281 503, Rr2 = 2447,9 Н
∑М2У = 0, -220Fшк + 50· Fr - Fa·d/2 + 115· R1r = 0,
-220·1267,1 + 50· 1293,5 - 1160·111/2 + 115· R1r = 0,
115· R1r = 248 467, Rr1 = 2421,5 Н
Проверка: ∑Fi(Y) = 0, -Fшк + R1r + Fr – R2r = 0
-1267,1 + 2421,5 + 1293,5 – 2447,9 = 0


0≡0 – абсолютное тождество, те. реакции определены верно.
Строим эпюру МУ
I участок ( 0<z1< 50 )
MУ(Z1)= -R2r · z1 (уравнение наклонной прямой)
MУ(Z1=0) = 0,
MУ(Z1=а=50) =-R2r· 105 = -2447,9 · 50= -122 395 Н·мм
II участок (0<z2< 65 )
MУ(Z2) = -R2r· (50 + z2) + Fa·d/2 + Fr z2 (уравнение наклонной прямой)
MУ(Z2= а=0 )= -R2r· 50 + 1160·111/2 = -122 395 + 64 380 = -58 015 Нмм
MУ(Z2= а=65 )= -2447,9· (50 + 65) + 1160·111/2 + 1293,5·65= -133 051 Нмм;
III участок (0<z3<105)
MУ(Z3)= -Fшк · z3 (уравнение наклонной прямой)
MУ(Z3=0) = 0
MУ(Z3= 2а=105)= -Fшк · 105 = -1267,1 · 105= 133 051 кН·м
Горизонтальная плоскость:
Определяем реакции опор:
∑М1Х = 0, -50Ft + 115· R2t = 0,
-50·3123 + 115· R2t = 0,
115· R2t = 156 150, Rt2 = 1357,8 Н
∑М2Х = 0, -65Ft + 115· R1t = 0,
-65·3123 + 115· R1t = 0,
115· R1t = 202 995, Rt1 = 1765,2 Н
Проверка: ∑Fi(Y) = 0, Ft - R1t– R2t = 0
-1357,8 + 3123 – 1765,2 = 0
0≡0 – абсолютное тождество, те. реакции определены верно.
Строим эпюру МX
I участок ( 0<z1< 65 )
MУ(Z1)= - R1t r · z1 (уравнение наклонной прямой)
MУ(Z1=0) = 0,
MУ(Z1=а=65) =- R1t · 65 = -1357,8 · 65= -88 257 Н·мм
Суммарный изгибающий момент вычисляется по формуле:
![]()
МИ1= 0
МИ2 = 150 897 Н·мм
МИ3= 133 051 Н·мм
МИ4 = 0
Опасным является сечение 2 , так как в нем одновременно действует наибольший изгибающий момент М = 150 897 Н·мм и крутящий момент Т =180 670 Н·мм.
Побор диаметра вала под колесом 3 по третьей гипотезе прочности
![]() = 235 397 Н·мм
= 235 397 Н·мм
Условие прочности по III гипотезе прочности
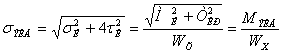 ≤[σ],
≤[σ],
![]() , отсюда
, отсюда 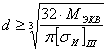 =
= ![]() , выбираем диаметр из стандартного ряда d = 42.
, выбираем диаметр из стандартного ряда d = 42.
Побор диаметра вала под подшипники по третьей гипотезе прочности
![]() = 224 380 Н·мм
= 224 380 Н·мм
Условие прочности по III гипотезе прочности
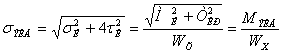 ≤[σ],
≤[σ],
![]() , отсюда
, отсюда 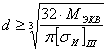 =
= ![]() ,
,
выбираем диаметр из стандартного ряда диаметров подшипников d = 40.
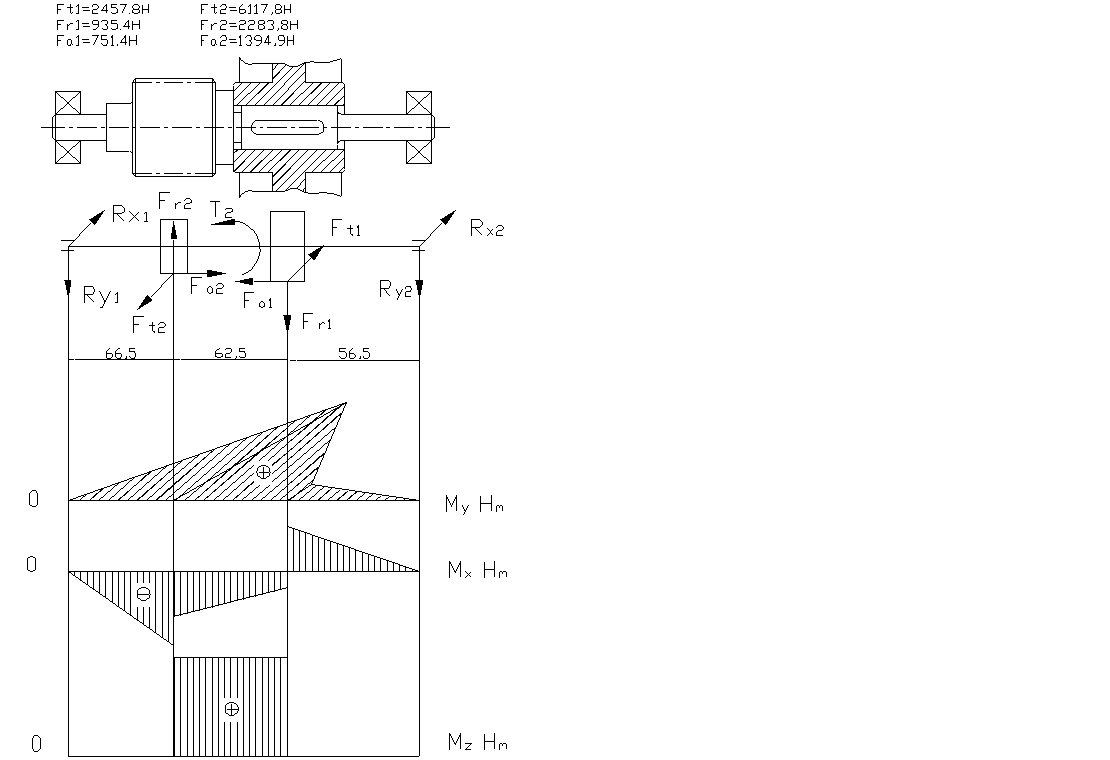
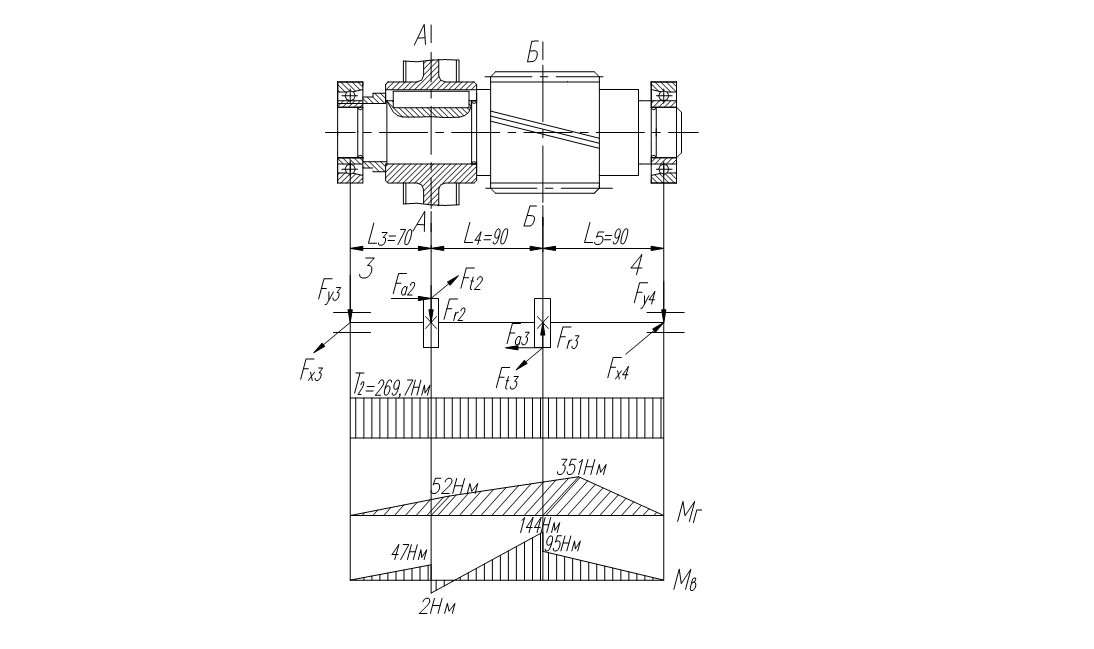
Рассмотрим вал №2:
Построение эпюр изгибающих моментов в вертикальной и горизонтальной плоскостях.
Вертикальная плоскость:
Определяем реакции опор:
∑М1У = 0, 63· Fr2Б - Fa·d/2 + 199· Fr2Т - 270· R2r = 0,
63· 1293,5 - 1160·209/2 + 199· 1888,4 - 270· R2r = 0,
270· R2r = 336 062,1, Rr2 = 1244,9 Н
∑М2У = 0,- 207· Fr2Б - Fa·d/2 - 71· Fr1Т + 270· R1r = 0,
-207· 1293,5 - 1160·209/2 - 71· 1888,4 + 270· R1r = 0,
270· R1r = 523 051, Rr1 = 1937 Н
Проверка: ∑Fi(Y) = 0, Rr1 - Fr2Б - Fr2Т + R2r = 0
1937– 1293,5 – 1888,4 + 1244,9 = 0
0≡0 – абсолютное тождество, те. реакции определены верно.
Строим эпюру МУ
I участок ( 0<z1< 63 )
MУ(Z1)= R1r · z1 (уравнение наклонной прямой)
MУ(Z1=0) = 0,
MУ(Z1=а=63) = R1r· 63 = 1937 · 63= 122 031 Н·мм
II участок (0<z2< 136 )
MУ(Z2) = R1r· (63 + z2) - Fa·d/2 - Fr2б z2 (уравнение наклонной прямой)
MУ(Z2= а=0 )= R1r· 63 - 1160·209/2 = 122 031 - 121 220 = 811 Н·мм
MУ(Z2= а=136 )= 1937· (63 + 136) - 1160·209/2 - 1293,5·136= 88 388 Н·мм;
III участок (0<z3<71)
MУ(Z3)= R2r· z3 (уравнение наклонной прямой)
MУ(Z3=0) = 0
MУ(Z3= 2а=71)= R2r · 71 = 1244,9 · 71= 88 388 кН·м
Горизонтальная плоскость:
Определяем реакции опор:
∑М1Х = 0, 63Ft2Б + 199· Ft1Т -270R2t = 0,
63·3123 + 199· 5188,24-270R2t = 0,
270· R2t = 1 299 209, R2t = 4552,62 Н
|
|
|


∑М2Х = 0, -207Ft2Б - 71· Ft1Т +270R1t = 0,
-207·3123 - 71· 5188,24-270R1r = 0,
270· R1t = 1 014 826, R1t = 3758,62 Н
Проверка: ∑Fi(Y) = 0, R1t – Ft2Б – Ft1Т + R2t = 0
4552,62 - 3123 – 5188,24 + 3758,62 = 0
0≡0 – абсолютное тождество, те. реакции определены верно.
Строим эпюру МX
I участок ( 0<z1< 63 )
MУ(Z1)= R1t · z1 (уравнение наклонной прямой)
MУ(Z1=0) = 0,
MУ(Z1=а=65) = R1t · 63 = 3758,62 · 63= 236 793 Н·мм
II участок (0<z2< 136 )
MУ(Z2) = R1t· (63 + z2) - Ft2б z2 (уравнение наклонной прямой)
MУ(Z2= а=0 )= R1t· 63 = 236 793 Н·мм
MУ(Z2= а=136 )= 3758,62 · (63 + 136) - 3123·136= 323 237,4 Н·мм;
III участок (0<z3<71)
MУ(Z3)= R2t· z3 (уравнение наклонной прямой)
MУ(Z3=0) = 0
MУ(Z3= 2а=71)= R2t · 71 = 4552,62 · 71 = 323 237,4 кН·м
Суммарный изгибающий момент вычисляется по формуле:
![]()
МИ1= 0
МИ2 = 266 388 Н·мм
МИ3= 335 104 Н·мм
МИ4 = 0
Опасным является сечение 3 , так как в нем одновременно действует наибольший изгибающий момент М = 355 104 Н·мм и крутящий момент Т =326 345 Н·мм.
Побор диаметра вала под колесом 5 по третьей гипотезе прочности
![]() = 482 286 Н·мм
= 482 286 Н·мм
Условие прочности по III гипотезе прочности
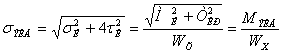 ≤[σ],
≤[σ],
![]() , отсюда
, отсюда ![]() =
= ![]() ,
,
принимаем диаметр из стандартного ряда диаметр вала под колесом 5 d=50 мм, диаметр вала под колесом 4 d=48 мм,
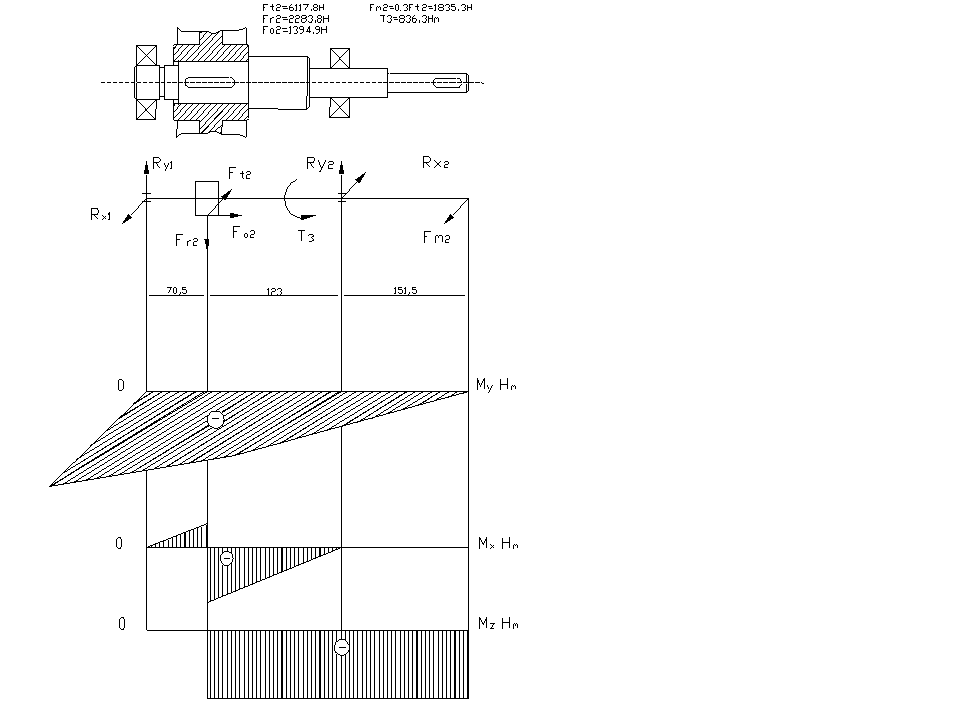
Рассмотрим вал №3:
Построение эпюр изгибающих моментов в вертикальной и горизонтальной плоскостях.
Вертикальная плоскость:
Определяем реакции опор:
∑М1У = 0, - 65· Frт - 133· R2r = 0,
65·1888,4 - 133· R2r = 0,
133· R2r = 122 746, Rr2 = 923 Н
∑М2У = 0, - 68· Frт - 133· R1r = 0,
68·1888,4 - 133· R1r = 0,
133· R1r = 128 411, Rr1 = 965,4 Н
Проверка: ∑Fi(Y) = 0, - R1r + Frт– R2r = 0
-923 + 1888,4– 965,4 = 0
0≡0 – абсолютное тождество, те. реакции определены верно.
Строим эпюру МУ
I участок ( 0<z1< 68 )
MУ(Z1)= -R2r · z1 (уравнение наклонной прямой)
MУ(Z1=0) = 0,
MУ(Z1=а=50) =-R2r· 68 = -БЬЛ 68= -65 647 Н·мм
Горизонтальная плоскость:
Определяем реакции опор:
∑М1Х = 0, -65·Ft + 133· R2t - 293·Fм = 0,
-65·5188,24 + 133· R2t - 293·4619,4 = 0,
133· R2t = 1 690 720, Rt2 = 12 712 Н
∑М2Х = 0, 68·Ft + 133· R1t - 160·Fм = 0,
68·5188,24 + 133· R2t - 160·4619,4 = 0,
133· R1t = 386 293, Rt1 = 2904,6 Н
Проверка: ∑Fi(Y) = 0, Rt1 + Ft – R2t + Fм = 0
2904,6 + 5188,24 – 12712 + 4619,4 = 0
0≡0 – абсолютное тождество, те. реакции определены верно.
Строим эпюру МX
I участок ( 0<z1< 65 )
MУ(Z1)= R1t · z1 (уравнение наклонной прямой)
MУ(Z1=0) = 0,
MУ(Z1=а=65) =R1t · 65 = 2904,6 · 65= 188 793 Н·мм
II участок (0<z2< 68 )
MУ(Z2) = R1t· (68 + z2) + FtТ z2 (уравнение наклонной прямой)
MУ(Z2= а=0 )= R1t· 65 = 188 793 Н·мм
MУ(Z2= а=68 )= 2904,6 · (63 + 68) + 5188,4·68= 739 104 Н·мм;
III участок (0<z3<160)
MУ(Z3)= Fм· z3 (уравнение наклонной прямой)
MУ(Z3=0) = 0
MУ(Z3= 2а=160)= Fм · 160 = 4619,4 · 160 = 739 104 кН·м


Суммарный изгибающий момент вычисляется по формуле:
![]()
МИ1= 0
МИ2 = 199 881 Н·мм
МИ3= 739 104 Н·мм
МИ4 = 0
Опасным является сечение 3, так как в нем одновременно действует наибольший изгибающий момент М = 739 104 Н·мм и крутящий момент Т =524 920 Н·мм.
Побор диаметра вала по третьей гипотезе прочности
![]() = 906 541 Н·мм
= 906 541 Н·мм
Условие прочности по III гипотезе прочности
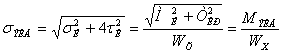 ≤[σ],
≤[σ],
![]() , отсюда
, отсюда ![]() =
= ![]() ,
,
диаметр вала под подшипники принимаем d = 60 мм
Уточненный расчет валов
Материал вала сталь 45:
σВ = 500 МПа;
στ = 280 МПа;
ττ = 150 МПа;
σ-1 = 250 МПа;
τ-1 = 150 МПа;
ψτ = 0;
Кσ = 1,6,
Кτ = 1,4,
εσ= ετ( при d=40мм)=0,73,
Входной вал (шпонка под колесом 3):
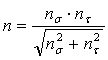 , [n] = 1,5 …3.
, [n] = 1,5 …3.
Запас прочности по напряжениям изгиба по III циклу напряжения:
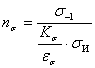
![]() ,
,
![]()
![]() = 6431мм3;
= 6431мм3;
![]() = 13 840 мм3;
= 13 840 мм3;
![]()
![]()
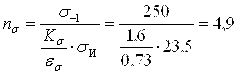
Запас прочности по напряжениям кручения
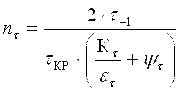
![]() ,
,
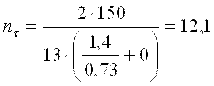 ,
,
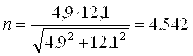 ,
,
так запас прочности больше трех, то диаметр вала можно уменьшить. По нормальному ряду
Промежуточный вал (шпонка под колесом 4):
εσ= ετ( при d=48мм)=0,7,
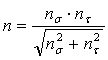 , [n] = 1,5 …3.
, [n] = 1,5 …3.
Запас прочности по напряжениям изгиба по III циклу напряжения:
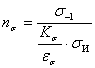
![]() ,
,
![]()
![]() = 9576,2мм3;
= 9576,2мм3;
![]() = 20 635,4 мм3;
= 20 635,4 мм3;
![]()
![]()

Запас прочности по напряжениям кручения

![]() ,
,
 ,
,
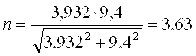 ,
,
так запас прочности больше трех, то диаметр вала можно уменьшить, следующий диаметр по стандартному ряду 45 мм.
![]() = 7744 мм3;
= 7744 мм3;
![]() = 16 890 мм3;
= 16 890 мм3;
![]()
![]()
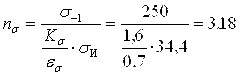
Запас прочности по напряжениям кручения

![]() ,
,
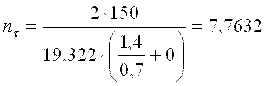 ,
,
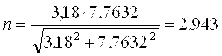 , следовательно оставляем диаметр 45 мм.
, следовательно оставляем диаметр 45 мм.
Промежуточный вал (шпонка под колесом 5):
εσ= ετ( при d=50мм)=0,7,
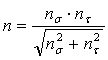 , [n] = 1,5 …3.
, [n] = 1,5 …3.
Запас прочности по напряжениям изгиба по III циклу напряжения:
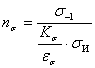
![]() ,
,
![]()
![]() = 10 976мм3;
= 10 976мм3;
![]() = 23 476 мм3;
= 23 476 мм3;
![]()
![]()
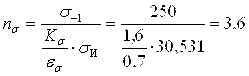
Запас прочности по напряжениям кручения

![]() ,
,
 ,
,
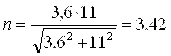 ,
,
так как запас прочности больше трех то диаметр вала можно уменьшить, принимаем следующий по нормальному ряду диаметр 48.
![]() = 9576,2мм3;
= 9576,2мм3;
![]() = 20 635,4 мм3;
= 20 635,4 мм3;
![]()
![]()
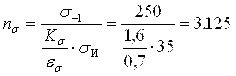
Запас прочности по напряжениям кручения

![]() ,
,
 ,
,
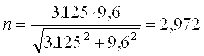 ,
,
оставляем диаметр вала 48 мм.
Выходной вал (шпонка под колесом 6):
εσ= ετ( при d=63 мм)=0,681,
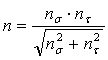 , [n] = 1,5 …3.
, [n] = 1,5 …3.
Запас прочности по напряжениям изгиба по III циклу напряжения:
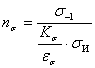
![]() ,
,
![]()
![]() = 21869мм3;
= 21869мм3;
![]() = 46873 мм3;
= 46873 мм3;
![]()
![]()
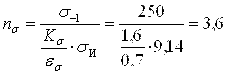
Запас прочности по напряжениям кручения

![]() ,
,
 ,
,
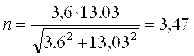 ,
,
так как мы не можем уменьшить диаметр исходя из особенности конструкции, то оставляем диаметр 63 мм.
Расчет подшипников
Для входного вала выбираем подшипники радиальные «Подшипник 408 ГОСТ 8338 - 75»:
Динамическая грузоподъемность С – 50,03 кН;
Статическая грузоподъемность С0 – 37 кН;
V = 1, при вращении внутреннего кольца;
Диаметр шарика Dw = 22,23 мм;
Частота вращения вала 483,333 об/мин;
Требуемый ресурс наработки 16704 часа;
Окружная сила Ft = 2 ·М2 / d2 =3123 H;
Радиальная сила - Fr = 1293,5 H;
Осевая сила - Fa1 = 1160H;
Rr1 = 2421,5 Н Rr2 = 2447,9 Н
Rt1 = 1765,2 Н Rt2 = 1357,8 Н
Суммарные реакции опор:
![]()
![]()
Осевая сила Fa нагружающая подшипник, равна внешней силе, действующей на вал. Осевую силу воспринимают оба подшипника на консольных концах вала, так как они ограничивают перемещение вала под действием этой силы.
Радиальная реакции подшипника приложена к оси вала в точке пересечения с ней нормали, проведенной через середины контактных площадок. Для радиальных подшипников эта точка расположена по середине ширины подшипника. Подшипник 1 наиболее нагружен так как он воспринимает большую нагрузку.
![]() /дунаев/
/дунаев/
Коэффициент осевого нагружения для радиального подшипника:
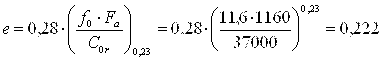 , отношение Fa/VFr = 1160/2997 = 0,387 > e. Окончательно принимаем:
, отношение Fa/VFr = 1160/2997 = 0,387 > e. Окончательно принимаем:
Х = 0,56, У = 0,44/е = 1,982.
Принимаем коэффициент динамичночти нагрузки Кб для редуктора равным 1,4, Температурный коэффициент Кт = 1 (tраб < 100°С). Тогда эквивалентная динамическая радиальная нагрузка:
Pr = (VXFr + YFa)· Кб· Кт = (1·0,56·2997 + 1,982·1160)·1,4·1 = 5569 Н.
Расчетный скорректированный ресурс подшипника при а1 = 1( вероятность безотказной работы 90%), а23 = 0,7 (обычные условия применения), к=3 (шариковый подшипник):
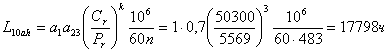 , условие выполняется.
, условие выполняется.
Для промежуточного вала выбираем подшипники радиальные «Подшипник 308 ГОСТ 8338 - 75»:
Динамическая грузоподъемность С – 31,9 кН;
Статическая грузоподъемность С0 – 22,7 кН;
V = 1, при вращении внутреннего кольца;
Диаметр шарика Dw = 15,08 мм;
Частота вращения вала 253,86 об/мин;
Требуемый ресурс наработки 16704 часа;
Осевая сила - Fa1 = 1160H;
Rr1 = 1937 Н Rr2 = 1244,9 Н
R1t = 3758,62 Н R2t = 4552,62 Н
Суммарные реакции опор:
![]()
![]()
Осевая сила Fa нагружающая подшипник, равна внешней силе, действующей на вал. Осевую силу воспринимают оба подшипника на консольных концах вала, так как они ограничивают перемещение вала под действием этой силы.
Радиальная реакции подшипника приложена к оси вала в точке пересечения с ней нормали, проведенной через середины контактных площадок. Для радиальных подшипников эта точка расположена по середине ширины подшипника. Подшипник 2 наиболее нагружен так как он воспринимает большую нагрузку.
![]() /дунаев/
/дунаев/
Коэффициент осевого нагружения для радиального подшипника:
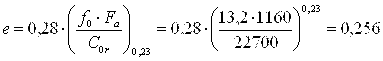 ,
,
отношение Fa/VFr = 1160/4720 = 0,246 < e. Окончательно принимаем:
Х = 1, У = 0.
Принимаем коэффициент динамичночти нагрузки Кб для редуктора равным 1,4, Температурный коэффициент Кт = 1 (tраб < 100°С). Тогда эквивалентная динамическая радиальная нагрузка:
Pr = (VXFr + YFa)· Кб· Кт = (1·1·4720 + 0·1160)·1,4·1 = 6608 Н.
Расчетный скорректированный ресурс подшипника при а1 = 1( вероятность безотказной работы 90%), а23 = 0,7 (обычные условия применения), к=3 (шариковый подшипник):
 ,
,
условие не выполняется, принимаем подшипник более тяжелой серии № 408
Динамическая грузоподъемность С – 50,3 кН;
Статическая грузоподъемность С0 – 37,0 кН;
V = 1, при вращении внутреннего кольца;
Диаметр шарика Dw = 22,23 мм;
![]() /дунаев/
/дунаев/
Коэффициент осевого нагружения для радиального подшипника:
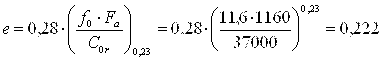 , отношение Fa/VFr = 1160/4720 = 0,246 > e. Окончательно принимаем:
, отношение Fa/VFr = 1160/4720 = 0,246 > e. Окончательно принимаем:
Х = 0,56, У = 0,44/е = 1,982.
Принимаем коэффициент динамичночти нагрузки Кб для редуктора равным 1,4, Температурный коэффициент Кт = 1 (tраб < 100°С). Тогда эквивалентная динамическая радиальная нагрузка:
Pr = (VXFr + YFa)· Кб· Кт = (1·0,56·4720 + 1,982·1160)·1,4·1 = 6919,25 Н.
Расчетный скорректированный ресурс подшипника при а1 = 1( вероятность безотказной работы 90%), а23 = 0,7 (обычные условия применения), к=3 (шариковый подшипник):
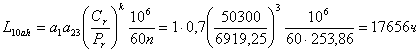 , условие выполняется.
, условие выполняется.
Для выходного вала выбираем подшипники радиальные «Подшипник 411 ГОСТ 8338 - 75»:
Динамическая грузоподъемность С – 78,7 кН;
Статическая грузоподъемность С0 – 63,7 кН;
V = 1, при вращении внутреннего кольца;
Частота вращения вала 150 об/мин;
Требуемый ресурс наработки 16704 часа;
Rr1 = 965,4 Н Rr2 = 923 Н
Rt1 = 2904,6 Н Rt2 = 12 712 Н
Суммарные реакции опор:
![]()
![]()
Радиальная реакции подшипника приложена к оси вала в точке пересечения с ней нормали, проведенной через середины контактных площадок. Для радиальных подшипников эта точка расположена по середине ширины подшипника. Подшипник 2 наиболее нагружен так как он воспринимает большую нагрузку.
Окончательно принимаем:
Х = 1, У = 0.
Принимаем коэффициент динамичночти нагрузки Кб для редуктора равным 1,4, Температурный коэффициент Кт = 1 (tраб < 100°С). Тогда эквивалентная динамическая радиальная нагрузка:
Pr = (VXFr + YFa)· Кб· Кт = 1·1·12745·1,4·1 = 17 844 Н.
Расчетный скорректированный ресурс подшипника при а1 = 1( вероятность безотказной работы 90%), а23 = 0,7 (обычные условия применения), к=3 (шариковый подшипник):
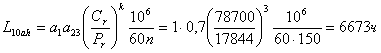 , условие не выполняется, назначем подшипник с большим диаметром №412:
, условие не выполняется, назначем подшипник с большим диаметром №412:
Динамическая грузоподъемность С – 85,6 кН;
Статическая грузоподъемность С0 – 71,4 кН;
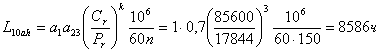 , за требуемое время эксплуатации подшипник придется поменять один раз.
, за требуемое время эксплуатации подшипник придется поменять один раз.
Похожие работы
... Для шестерни: Для колеса: Тогда расчетное контактное напряжение определяем по формуле (3.10 [1]) = 0.45(481+428)=410 МПа. 2.2 Расчет быстроходной ступени двухступенчатого зубчатого редуктора. 2.2.1 Межосевое расстояние определяем по формуле (3.7 [1]) , мм где: Ка – для косозубых колес Ка = 43; u1 – передаточное отношение первой ступени; Т2 – крутящий момент второго ...
... работы активно используется знания из ряда пройденных предметов : механики, сопротивления материалов ,технологий металлов и др. Объектом курсового проекта является привод с цилиндрическим двухступенчатым редуктором с раздвоенной быстроходной ступенью, использующие большинство деталей и узлов общего назначения. 1 Кинематический расчет 1.1 Находим момент на тихоходной ступени: РВЫХ = Тw; ...
... Муфты типа МУВП позволяют смягчать ударные нагрузки и рывки за счёт упругих элементов в составе муфты, кроме того, они допускают некоторые неточности сборки. Для соединения быстроходного вала редуктора с валом электродвигателя выбираем муфту упругую втулочно-пальцевую (МУВП) ГОСТ 21424-75. Принимаем муфту МУВП 250-40-1 У3 ГОСТ 21424-93. Номинальный крутящий момент Мкр., Н×м = 250 Частота ...
... 9.33 91.65 5 0.9653 3 194.6 20.37 9.01 442.31 3.395 0.92 4 57 5.97 8.25 1374.4 Проверка : - Условие выполняется2 Расчет передач 2.1 Расчет цилиндрических зубчатых передач 2.1. 1 Определение допускаемых напряжений По условию задания материал ...

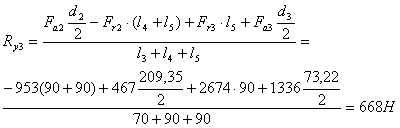
0 комментариев