Первый столбец интервал оценок, остальные – балл за выраженность качества (реализована шкала интервалов)

1.         Первый столбец интервал оценок, остальные – балл за выраженность качества (реализована шкала интервалов).

При распределении испытуемых по классам в один класс попадают сильно различающиеся по первичным оценкам испытуемые. Мы рассмотрели различные приемы перевода качественных психологических признаков в количественные выражения. Следует отметить, что при описании психологических явлений необходимо всегда отдавать себе отчет в том, какая именно шкала используется, поскольку каждый способ обработки экспериментальных данных рассчитан на определенный тип шкал.

Применение математических методов к неадекватным данным приводит к странным, а часто и ложным результатам. Квантификация сложных и далеко не однозначных психологических характеристик накладывает немало ограничений на математические операции с их измерениями.

Математик работает с простыми числами, психолог обязан помнить, что в действительности скрывается за величинами, которыми он оперирует.

1) Первое ограничение – соразмерность количественных показателей, фиксированных разными шкалами в рамках одного исследования. Более сильная шкала отличается от слабой тем, что допускает более широкий диапазон математических операций с числами. Все, что допустимо для слабой шкалы допустимо и для более сильной, но не наоборот. Поэтому, смешение в анализе мерительных эталонов разного типа приводит к тому, что не используются возможности сильных шкал.

2) Второе ограничение связано с формой распределения величины фиксированных описанными выше шкалами, которое предполагается нормальным. Для нормального распределения оценки меры рассеяния совпадают: Мо=Ме=М, в скошенном хвосты распределения не влияют на среднюю (М).

Таким образом, необходимо внимательно изучать форму распределения с точки зрения его отклонения от нормального.

II. Используя понятия интегральной функции распределения и определенного интеграла можно записать

¦ (x) = F¢ (x) или F (x) = p (x₁ < X < x₂) = .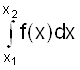

Если 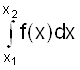 определяет заштрихованную область в соответствующих пределах, то

p (х < Х < х + Dх) » ¦ (х) Dх.

Это соотношение можно представить в виде простого геометрического толкования для каждого класса.

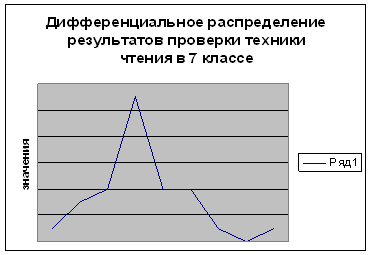
Рис. 1 График дифференциального распределения результатов проверки техники чтения в 7 классе

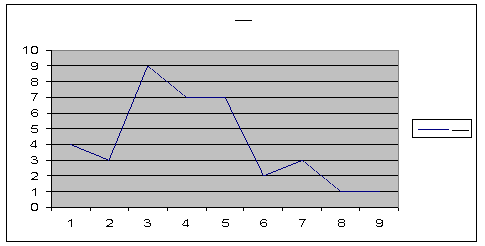
Рис. 2 Результаты дифференциального распределения результатов проверки техники чтения в 8 классе

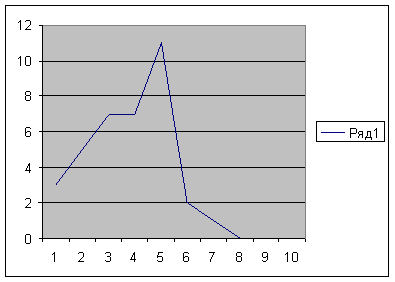
Рис. 3 Результаты дифференциального распределения результатов проверки техники чтения в 9 классе.

Для дискретной случайной величины справедливо следующее равенство:

F (x) = P (X < x) = P (-¥ < X < x) = ,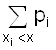

где суммирование распространяется на х_i < х.

В промежутке между двумя последовательными значениями Х функция F (х) постоянна. При переходе аргумента х через значение х_i F (х) скачком возрастает на величину p (Х = х_i).

Рассмотрим p (х₁ £ Х < х₂). Если х₂ > х₁, то очевидно, что

p (Х < х₂) = p (Х < х₁) + p (х₁ £ Х < х₂).

Тогда

p (х₁ £ Х < х₂) = p (Х < х₂) - p (Х < х₁) = F (х₂) - F (х₁),

т.е. вероятность попадания случайной величины в интервал [х₁; х₂) равен разности значений интегральной функции граничных точек.

Последнее условие можно использовать для нахождения вероятности p (Х = х₁) для непрерывной случайной величины. Для этого рассмотрим предел

p (X = x₁) = ,

т.е. если закон распределения случайной величины есть функция непрерывная, то вероятность того, что случайная величина примет заранее заданное значение, равна нулю.

Здесь видно различие между дискретными и непрерывными случайными величинами. Для дискретных случайных величин, для каждого значения случайной величины существует своя вероятность. И для него справедливо утверждение: событие, вероятность которого равна нулю, невозможно. Для непрерывной случайной величины это утверждение неверно. Как показано, вероятность того, что Х = х₁ (где х₁- заранее выбранное число) равна нулю, это событие не является невозможным.

В этой связи невозможно построение графика интегрального распределения поэтому нами будет построена кривая интегрального распределения для 7,8, 9 классов.

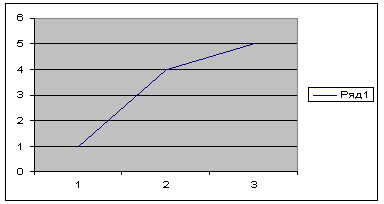
Рис. 4 График интегрального распределения результатов техники чтения для 7,8, 9 класса.

Таким образом, можно сделать следующий вывод, что наиболее достоверна дифференциальное распределение полученных результатов.

Задание №3.

Выборка объемом 30 человек, разбитая на две равные группы по признаку пола, прошла функциональную диагностику мозговой активности, в результате которой у 13 женщин и 4 мужчин было выявлено доминирование правого полушария, а у 2 женщин и 11 мужчин — доминирование левого полушария. Проверьте гипотезу о связи функциональной асимметрии головного мозга с полом.

Решение:

Поскольку в обеих выборках n₁ и n₂> 11 и диапазоны разброса значений в двух выборках не совпадают между собой, мы можем воспользоваться самым простым критерием для сопоставления двух выборок – критерием Q Розенбаума. Объемы выборок различаются менее чем на 10 человек, так, что ограничение о примерном равенстве выборок также не препятствует нам.

Таблица 1. Показатели выраженности функциональной асимметрии у мужчин и женщин

	Группа 1 – мужчины (n=15 человек)	Группа 2 – женщины (n=15 человек)
Доминирование правового полушария	4	13
Доминирование левого полушария	11	2

Данные в таблице 1 расположены по степени доминирования того или иного полушария в мужской или женской выборке. Первым более высоким является ряд значений в женской выборке.

Средняя величина в мужской и женской выборке идентична и равна 7,5.

Сформулируем гипотезы.

Формулирование гипотез систематизирует предположения исследователя и представляет их в четком и лаконичном виде [5; с. 24]. Статистические гипотезы подразделяются на нулевые и альтернативные.

Нулевая гипотеза – это гипотеза об отсутствии различий. Она обозначается как Н₀ и называется нулевой потому, что содержит число 0:

X₁-X₂ =0, где X₁, X₂ – сопоставления значение признаков. Таким образом, нулевая гипотеза – это то, что мы хотим опровергнуть, если перед нами стоит задача доказать значимость различий.

Альтернативная гипотеза – это гипотеза о значимости различий. Она обозначается как Н₁. Альтернативная гипотеза – это то, что мы хотим доказать, поэтому иногда ее называют экспериментальной гипотезой.

Сформулируем основные гипотезы:

Н₀: Функциональная асимметрия головного мозга у мужчин не выражена в большей степени, чем у женщин.

Н₁: Функциональная асимметрия головного мозга у мужчин выражена в большей степени, чем у женщин.

Сопоставим ряды значений для определения S₁ и S₂.

max 2 = 13

S₁ =0

min 1 =4

S₂ =1

Производим подсчет эмпирического значения Q_эмп = S₁+S₂ = 0+1 = 1

По таблице 1 Приложения I [5; с. 316] определяем критическое значение Q для данных n₁ и n₂. Если Q_эмп равно Q_0,05 или превышает его, Н₀ отвергается.

В данном случае Q_кр = 6

6 (p≤0,01)

Q_эмп<Q_кр

Следовательно принимается гипотеза Н₀ и отвергается гипотеза Н₁.

Функциональная асимметрия головного мозга у мужчин не выражена в большей степени, чем у женщин, следовательно, функциональная асимметрия головного мозга не зависит от признака пола.

Список используемой литературы

1.   Ермолаев О.Ю. Математическая статистика для психологов/ О.Ю. Ермолаев.- М.: МПСИ, Флинта, 2002. - 336 с.

2.   Кутейников А.Н., Математические методы в психологии/А.Н. Кутейников.- М.: Речь, 2008. - 172 с.

3.   Митина О.В., Математические методы в психологии. Практикум: Учебное пособие/О.В. Митина.- М.: Издательство Аспект – пресс, 2008. - 238 с.

4.   Наследов А.Д., Математические методы в психологии: Учебное пособие/ А.Д. Наследов.- Спб: Речь, 2004. - 232 с.

5.   Сидоренко Е.В., Методы математической обработки в психологии/ Е.В. Сидоренко.- М.: Речь, 2006. - 350 с.

6.   Суходольский Г.В., Математические методы в психологии: Учебное пособие/ Г.В. Суходольский.- М.: Гуманитарный центр, 2008. - 284 с.

7.   Титкова Л.С., Математические методы в психологии/ Л.С. Титкова.- Владивосток: Издательство ДВГУ, 2002. - 140 с.

^1. Титкова Л. С., Математические методы в психологии/ Л. С. Титкова.- Владивосток: Издательство ДВГУ, 2002.- с. 12.

² Там же, с. 12

³ Там же, с. 12