Навигация
Вычислить коэффициент полной корреляции между частями теста используя формулу
4. Вычислить коэффициент полной корреляции между частями теста используя формулу
Пирсона:
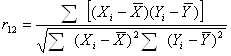 ,
,
где![]() - разность между значениями варианты и средней арифметической величиной нечетной части теста,
- разность между значениями варианты и средней арифметической величиной нечетной части теста, ![]() - разность между значениями варианты и средней арифметической величиной четной части теста.
- разность между значениями варианты и средней арифметической величиной четной части теста.
Вычисляем коэффициент полной корреляции между частями теста используя формулу
Пирсона:
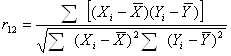 , =
, =![]() =
= ![]() = 0,795
= 0,795![]() 0,8
0,8
0,8 коэффициент полной корреляции между частями теста.
5. Вычислить коэффициенты надежности, используя следующие формулы:
а) Спирмана - Брауна: где ![]() - коэффициент корреляции по Пирсону,
- коэффициент корреляции по Пирсону, ![]() - стандартные отклонения нечетных и четных задач,
- стандартные отклонения нечетных и четных задач, ![]() - общее количество задач в тесте.
- общее количество задач в тесте.
6. Сделайте вывод о надежности теста Равена.
а) Спирмана - Брауна:
![]() =
= ![]() = 0,88
= 0,88 ![]() 0,9
0,9
б) Фланагана:
![]() =
= ![]() =
= ![]() =
= ![]()
Вывод: тест Равенна можно считать надежным, так как коэффициенты надежности приближаются к единице.
4. СТАНДАРТИЗАЦИЯ ТЕСТОВЫХ ШКАЛТеоретическая справка
Стандартизация тестовых шкал – это создание таких критериев (таблиц), по которым можно будет преобразовывать первичные результаты выполнения теста в относительные оценки.
Например, испытуемый выполнил 16 заданий теста математических достижений из 32 и получил за это 16 баллов из 32 максимально возможных. Таким образом, получается, что он выполнил половину всех заданий, - 50% . Значит ли это, что его достижения можно оценить как СРЕДНИЙ УРОВЕНЬ? Ответ на этот вопрос будет зависеть от того, с чем именно мы будем сравнивать полученный испытуемым результат, с чем будем его соотносить. Если соотносить с максимально возможным баллом, то действительно можно будет сказать, что у испытуемого средний уровень математических достижений. Ну, а сели сравнить с результатами других испытуемых? Например, одинаковых с ним по возрасту, полу, социальному положению и т.п.? Вполне может оказаться, что в этом случае наш испытуемый имеет низкий или высокий уровень достижений. Все будет зависеть от того, сколько еще людей из сравниваемой выборки набрали такие же результаты, сколько - набрали ниже, сколько - набрали выше. Таким образом, во-первых, необходимо иметь данные о результативности выполнения теста определенной выборкой испытуемых, с которой мы будем соотносить наши результаты. А во-вторых, эти данные о результативности мы должны как-то разделить на равные уровни по степени результативности. При этом количество уровней может быть разным – 5 уровней результативности, 9, 10 или 100. И затем, сравнив полученные конкретным испытуемым баллы, мы можем определить его место в той выборке, с которой его соотносим. В данной работе предлагается познакомиться с методами разделения распределения результативности выполнения теста на отдельные уровни.
1.Наиболее простым способом нормирования (разделения распределения на уровни) является шкала процентилей. Процентиль – это точка на числовой шкале, состоящей из 100 уровней. Ранг показателя в процентилях определяется процентным отношением в нормативной группе тех испытуемых, которые получили более низкий показатель. Например, 15 процентиль (Р15)означает, что 15% из нормативной выборки получили показатели ниже данного. Вычисление процентиля немногим сложнее, чем его определение. Оно выражается следующей формулой:
Pp = L + ![]() ,
,
где Pp - искомая величина на шкале процентилей, L - фактическая нижняя граница интервала оценок, содержащего частоту rn, pn - произведение общего количества данных n на относительную частоту (т.е.p/100), f cum - накопленная к L частота, f - частота оценок в интервале, содержащем оценку rn.
Расчет рекомендуется проводить по следующему алгоритму:
а) Упорядочить полученные результаты по возрастанию.
б) Каждому первичному результату приравнять его частоту, т.е.количество испытуемых получивших такой же результат;
в) Произвести накопление частот
г) Подставить значения в формулу.
ПРИМЕРПреподаватель предложил 125 учащимся контрольное задание, состоящее из 40 вопросов. В качестве оценки теста выбиралось количество вопросов, на которые были получены правильные ответы. Распределение частот различных результатов приводится в таблице № 4. Необходимо определить каков 25-й процентиль в группе 125 оценок, т.е. чему равен Р25. Р25 – это точка, ниже которой лежат 25% 125 оценок.
Таблица № 4.
Оценки по тесту и их частоты.
| оценки по тесту | частота f | накопленная частота fcum |
| 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 | 1 1 3 5 9 8 17 23 24 18 10 3 1 0 2 | 125 124 123 120 115 106 98 81 58 34 16 6 3 2 2 |
Вычисление любого процентиля упростится, если построить распределение накопленных частот. Накопленные частоты к любой заданной оценке представляют собой суммарное количество частот на этой оценке и ниже ее. В третьем столбце таблицы указаны накопленные частоты для 125 оценок контрольного задания. Так, например тестовую оценку 33 и меньше получило 106 учащихся.
Вычисление Р25 можно выполнить за 5 шагов:
Шаг 1. r= 0,25, rn = 0,25n =0,25X125 = 31,25
Шаг 2. Найти фактическую нижнюю границу разряда оценок, содержащую испытуемого с оценкой 31,25 снизу: так как 16 человек имеют оценки 28 или меньше, а 34 – оценки 29 или меньше, то частота 31,25 лежит в интервале разряда оценок 28,5- 29,5.
L = 28,5
Шаг 3. Вычесть накопленную к L частоту из 31,25
31,25 – 16 = 15,25
Шаг 4. Разделить результат 3-го шага на частоту f в интервале, содержащем оценку 31,25
![]() = 0,85
= 0,85
Шаг 5. Прибавить результат 4-го шага к L
Р25 = 28,5 + 0,85 = 29,35
Шкала процентилей позволяет оценить отдельный индивидуальный результат относительно других индивидуальных результатов в исследуемой выборке. Самым большим недостатком шкалы процентилей является то, что она не отражает формы первичного распределения результатов. Распределение процентилей всегда равномерно (прямоугольно), тогда как распределение для многих тестов приближается к нормальному и небольшие отклонения от среднего значения сильно увеличиваются процентилями, а относительно большие отклонения, наоборот, сжимаются. Процентили могут таким образом исказить результаты и поэтому их использование не рекомендуется.
2. Наиболее распространенными преобразованиями первичных оценок являются центрирование и нормирование посредством среднеквадратических отклонений (z-преобразование). Под центрированием понимается линейная трансформация величин признака, при которой средняя величина распределения становится равной нулю. Так, если при обследовании группы испытуемых с помощью вновь разрабатываемого теста, средний результат по группе равен 17 «сырых» баллов, то эта величина может быть выбрана в качестве центра отсчета шкалы, в обе стороны от которой симметрично располагаются значения больше и меньше среднего. Для z-преобразования применяется следующая формула:
![]()
где![]() - разность между первичным результатом тестового измерения и средней арифметической величиной,
- разность между первичным результатом тестового измерения и средней арифметической величиной, ![]() - стандартное отклонение для данной выборки.
- стандартное отклонение для данной выборки.
Неудобство дальнейшей работы со стандартной шкалой состоит в том, что приходится оперировать отрицательными и положительными величинами, а также нулем.
От стандартной z-шкалы легко осуществить переход к любой другой, более удобной шкале. Для этого используется линейное преобразование типа
![]() ,
,
где a>0,0, константы a и b – произвольные действительные числа, выбор которых определяется исключительно удобством дальнейшей работы со шкалой.
В практике психологического тестирования используют ряд так называемых нормализованных шкал: T-шкала, шкала Векслера, шкала Амтхауэра, шкала стенов, шкала станайнов и др.
Задание № 4 Стандартизация тестовых шкал
Оценки по тесту и их частоты
| оценки по тесту | частота f | накопленная частота fcum |
| 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 | 1 1 3 5 9 8 17 23 24 18 10 3 1 0 2 | 125 124 123 120 115 106 98 81 58 34 16 6 3 2 2 |
На основе данных таблицы рассчитываем процентили: Pp = L + ![]() ,
,
Шаг 1. Рр =5/100х125=6,25
Шаг 2. Находим нижнюю границу разряда оценок содержащую испытуемого с оценкой 6,25 снизу: так как 6 человек имеют оценки 27 или меньше, а 16 человек – оценки 28 или меньше, то частота 6,25 лежит в интервале (27-28) следовательно, L=(27+28)/2=27,5.
Шаг 3. Вычитаем накопленную к L частоту из 6,25 6,25-6=0,25,где 6= f cum
Шаг 4. Разделим результаты третьего шага на частоту f в интервале, содержащим оценку 6,25 0,25/10=0,05, где f = 10.
Шаг 5.Р5=27,5+0,025=27,525![]() 27,53
27,53
Таким, образом, 5 % испытуемых имеют оценку 27,53 и ниже
Р10=27,5+(12,5-6)/10=27,5+0,65=28,15
Р20=28,5+(25-16)/18=28,5+0,5=29
Р30=29,5+(37,5-34)/24=29,5+0,145![]() 29,65
29,65
Р40=29,5+(50-34)/24=29,5+0,66![]() 30,17
30,17
Р50=30,5+(62,5-58)/23=30,5+0,195![]() 30,7
30,7
Р60=30,5+(75-58)/23=30,5+0,74![]() 31,24
31,24
Р70=31,5+(87,5-81)/17=31,5+0,38![]() 31,88
31,88
Р80=32,5+(100-98)/8=32,5+0,25= 32,75
Р90=33,5+(112,5-106)/9=33,5+0,72= 34,2
Р95=34,5+(118,75-115)/5=34,5+0,75= 32,25
Р100=38
Задание 4. Построение шкалы процентилей
Цель задания: овладение приемами стандартизации тестовых шкал на примере построения шкалы процентилей.
Оснащение: микрокалькулятор, таблица первичных результатов (таблица № 4).
Порядок работы:
1. На основе данных таблицы № 4, рассчитать P1, P5, P10, P20, P30, P40, P50, P60, P70, P80, P90, P95, P100.
2. На основе полученных данных построить шкалу процентилей.
24 38
P1 P100
Задание 5. Построение нормализованных шкал
Цель: овладение приемами преобразования первичных результатов в нормализованные шкалы.
Оснащение: микрокалькулятор, таблица первичных результатов (таблица №4).
Порядок работы:
1. Произвести линейное преобразование первичных результатов (z-трансформацию):
1) вычислить среднюю арифметическую величину (![]() );
);
2) рассчитать среднеквадратическое (стандартное) отклонение по формуле:
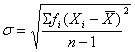 ,
,
где ![]() - разность между значениями варианты и средней арифметической величиной,
- разность между значениями варианты и средней арифметической величиной, ![]() - частота варианты,
- частота варианты, ![]() - количество вариант.
- количество вариант.
1. Произвести линейное преобразование первичных результатов (z-трансформацию):
| Частота |
|
|
|
|
| 1 | 38 | 7 | 49 | 49 |
| 1 | 37 | 6 | 36 | 36 |
| 3 | 36 | 5 | 25 | 75 |
| 5 | 35 | 4 | 16 | 80 |
| 9 | 34 | 3 | 9 | 81 |
| 8 | 33 | 2 | 4 | 32 |
| 17 | 32 | 1 | 1 | 17 |
| 23 | 31 | 0 | 0 | 0 |
| 24 | 30 | -1 | 1 | 24 |
| 18 | 29 | -2 | 4 | 72 |
| 10 | 28 | -3 | 9 | 90 |
| 3 | 27 | -4 | 16 | 48 |
| 1 | 26 | -5 | 25 | 25 |
| 0 | 25 | -6 | 36 | 0 |
| 2 | 24 | -7 | 49 | 98 |
![]() = 465/15=31
= 465/15=31 ![]() = 727
= 727
2) рассчитаем среднеквадратическое (стандартное) отклонение по формуле:
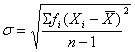 ,
,
где ![]() - разность между значениями варианты и средней арифметической величиной,
- разность между значениями варианты и средней арифметической величиной, ![]() - частота варианты,
- частота варианты, ![]() - количество вариант.
- количество вариант.
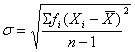 =
=![]() =
=![]() =
=![]() =7,206
=7,206
2) произвести линейное преобразование по формуле:
![]() ,
,
где![]() - разность между первичным результатом тестового измерения и средней арифметической величиной,
- разность между первичным результатом тестового измерения и средней арифметической величиной, ![]() - стандартное отклонение для данной выборки.
- стандартное отклонение для данной выборки.
Результаты вычислений занести в таблицу.
|
| z | T | IQ | Z |
| 38 | 0,96 | 59,6 | 114,4 | 109,6 |
| 37 | 0,83 | 58,3 | 112,5 | 108,3 |
| 36 | 0,69 | 56,9 | 110,4 | 106,9 |
| 35 | 0,55 | 55,5 | 108,3 | 105,5 |
| 34 | 0,41 | 54,1 | 106,2 | 104,1 |
| 33 | 0,28 | 52,8 | 104,2 | 102,8 |
| 32 | 0,14 | 51,4 | 102,1 | 101,4 |
| 31 | 0 | 50 | 100 | 100 |
| 30 | -0,14 | 48,6 | 97,9 | 98,6 |
| 29 | -0,28 | 47,2 | 95,8 | 97,9 |
| 28 | -0,41 | 45,9 | 93,8 | 95,9 |
| 27 | -0,55 | 44,5 | 91,7 | 94,5 |
| 26 | -0,39 | 43,1 | 89,6 | 93,1 |
| 25 | -0,83 | 41,7 | 87,5 | 91,7 |
| 24 | -0,96 | 40,4 | 85,6 | 90,4 |
1) T-шкала ![]() ;
;
2) Шкала Векслера ![]() ;
;
3) Шкала Амтхауэра ![]() .
.
[1] 6,63 – это критическое значение критеря хи-квадрат с 1 степенью свободы и при ρ = 1%.
Похожие работы
... задач: задачи с предписанными ответами, так называемые закрытые задачи, и задачи со свободными ответами, так называемые открытые задачи. В большинстве нормированных и стандартизированных, то есть психометрически обоснованных, психологических методик используются задачи первого класса. Это относится не только к тестам способностей, интеллектуального развития и др., но и к стандартизированным ...
... по тесту Роршаха Дж. Экснера, печальным следствием этих дискуссий явилось образование пропасти между психологами, занимающимися изучением личности, что отразилось в укоренившемся за рубежом делении психодиагностических методик на объективные и проективные. В соответствии с такой классификацией объективные методики считаются созданными на основе фундаментальных принципов измерения, неодократно ...
... , не выходя из дома, извлекая необходимую информацию из всемирной паутины, а также получить интернет-консультацию от психотерапевта. 3. Правила и ограничения в применении компьютеров в психологической диагностике Несмотря на то, что компьютеры, бесспорно, открывают путь для беспрецедентных усовершенствований всех аспектов психологической диагностики, в некоторых случаях их применение ...
... нарушения имеются с такого раннего периода, как только это могло быть обнаружено, без предшествующего периода нормального развития. 3. ДИАГНОСТИЧЕСКАЯ ПРОГРАММА ОБСЛЕДОВАНИЯ ДЕТЕЙ ДОШКОЛЬНОГО ВОЗРАСТА С НАРУШЕНИЕМ ПСИХОЛОГИЧЕСКОГО РАЗВИТИЯ Цель: анализ психического развития ребенка дошкольного возраста с нарушением психологического развития. Задачи: 1. Установление ...

0 комментариев