Суждение как логико-структурная форма мышления

МИНИСТЕРСТВО ВНУТРЕННИХ ДЕЛ РОССИЙСКОЙ ФЕДЕРАЦИИ

БЕЛГОРОДСКИЙ ЮРИДИЧЕСКИЙ ИНСТИТУТ

Кафедра гуманитарных и социально-экономических дисциплин

Дисциплина: "Логика"

ЛЕКЦИЯ

 

по теме: " Суждение как логико-структурная форма мышления "

Подготовил:

Слушатель 555 группы

факультета юриспруденция

Моргунов И.Т.

Белгород – 2008

Содержание

Вопрос № 1. Простые категорические суждения и их структура. Отношения между простыми суждениями.................................................................................... 3

Вопрос № 2. Сложные суждения и их виды. Методика анализа сложных суждений 11

Вопрос № 3. Понятие модальности суждения. Классификация видов суждений по модальности.................................................................................................. 31

Список используемой литературы............................................................... 39

Вопрос № 1. Простые категорические суждения и их структура. Отношения между простыми суждениями

Мир вещей не только су­ществует как реальность, но вещи в мире всегда находятся во взаимной свя­зи друг с другом. В этом смысле форма мышления, отражающая связи вещей, называется суждением. Логически связи вещей выражаются в том, что в суждении они либо утверждаются, либо отрицаются. Таким образом, суж­дение есть форма мышления, в которой утверждается или отрицается сам факт су­ществования предмета, а также утверждаются или отрицаются от­ношения между предметами. При этом данные высказывания могут выступать как истинные или ложные. Предметно суждения выражаются с помощью повествовательных предложений (не вопросительных и не восклицатель­ных!).

Нетрудно увидеть, что любая связь есть как минимум связь двух предметов. Следовательно, суждение есть как минимум связь двух понятий, одно из которых называется субъектом суждения S (от лат. subjectum – то, о чем говорится в предложении),[1] а другое – предикатом суждения P (от лат. praedicatum – то, что характеризует субъект суждения).[2] В субъекте суждения, таким образом, отражается сам целостный предмет, а в предика­те – признак предмета. Субъект суждения и предикат суждения называются терминами суждения. Термины суждения соединяются друг с другом при помощи связки, назначение которой состоит либо в утверждении ("есть", "является"), либо в отрицании ("не есть", "не является") факта отношения между субъектом и предикатом суждения. Такие суждения принято называть простыми.

Пример:

Высказывание "Всякое преступление есть противоправное дея­ние" представляет собой суждение. Действительно, здесь в повествова­тельной форме предложения утверждается некоторое отноше­ние: "Все преступления являются противоправными деяниями". Субъектом суждения в данном случае выступает словосочетание "Все преступления" ("Кто", "Что" является?), а предикатом суждения – словосочетание "Противоправные деяния" ("Кем", "Чем" является?). Следовательно, субъект суждения всегда вы­ражен в предложении логическим подлежащим, находящимся в именитель­ном падеже ("Кто?", "Что?").

Пример:

Высказывание "Белеет парус одинокий в тумане моря голубом" также представляет собой суждение. Однако это высказывание целесообразно предварительно перефразировать: "Одинокий парус является предметом, белеющим в голубом тумане моря". И тогда субъект будет выражен словосочетанием "Одинокий парус", предикат – словосочетанием "Предмет, белеющий в голубом тумане моря", а связка – словом "Является".

Пример:

Высказывание "Нет повести печальнее на свете, чем повесть о Ромео и Джульетте" представляет собой суждение. Отрицание "Нет" свидетельствует о том, что данное суждение отрицательное. Следовательно, в нем наличествует отрицание, которое может быть выражено словосочетанием "Не является". Отсю­да исходное высказывание можно перефразировать так: "Все повес­ти на свете не являются повестями более печальными, чем по­весть о Ромео и Джульетте". Субъект суждения здесь – "Все повести на све­те", предикат суждения – "Все повести более печальные, чем повесть о Ромео и Джульетте" [3], а связка суждения – "Не являются".

Как видим, предложения, выраженные средствами русского языка, могут быть самыми разнообразными, однако логический строй (логическая форма) суждения является всегда одним и тем же: субъект (логическое подлежащее), предикат (логическое сказуемое) и логическая связка (утверждение или отрицание). Поэтому прежде чем осущест­влять какие-либо логические операции с тем или иным суждением, необходимо перевести исходное высказывание в логическую форму суждения с явно выраженным субъектом (логическим подлежащим) в именительном падеже ("Кто?", "Что?"), с явно обозначенным предикатом (логическим сказуемым), выраженным предметно через соответ­ствующее имя существительное, и с фиксированной, словесно выраженной, связкой ("Является", "Не является"). Такое простое суждение символически можно выразить или (S есть P), т.е. (S – P); или (S не есть P), т.е. (ù (S – P)).

Все приведенные выше примеры суждений являются примерами так называемых атрибутивных суждений, канонической формулой которых и является как раз формула (S – P). Однако надо иметь в виду, что наряду с простыми атрибутивными суждениями в логике существуют также простые суждения об отно­шениях (или реляционные) и простые суждения существования (или экзистенциальные) (см. наст. изд., схема 9, стр. 52). Ответственной за форму простого суждения является в каждом данном случае форма предиката суждения.

Заметим, что в суждениях об отношениях обычно фиксируются отношения равенства, неравенства, родства, про­странственные, временные, причинно-следственные и др.

Пример:

Высказывание "Семен – отец Ивана" представляет собой суждение с отношени­ем родства, а высказывание "Москва старше Петербурга" – суждение с временным отношением.

В суждениях существования (экзистенциальных) выражается суще­ствование или несуществование чего-либо.

Пример:

"Преступник был вооружен"; "Нельзя объять необъятное".

Нетрудно заметить, что любой вид простого суждения в принципе может быть сведен к простому атрибутивному суждению за счет изменения формы предиката, что конкретизируется в виде словесной перефразировки исходного высказывания, ибо любой вид суждения – это всегда или утверждение, или отрицание. В силу этого утверждение и отрицание называются в логике качествами суждения. Непо­средственными выразителями качества суждения всегда выступает связка суждения, обычно выражаемая словами "является" или "не является". Вместе с тем, наряду с качеством, суждениям присуще и количество, что выражается словами "все" и "некоторые". Слова "все" и "некоторые" называются в логике кванторными словами. Кванторные слова применяются в суждении только вместе с субъектом и относятся только к последнему.

Суждения, количественно фиксируемые кванторным словом "Все", называются определенными ("Все слушатели БЮИ МВД РФ изучают логику"); суждения, количественно фиксируемые кванторным словом "Некоторые", называются неопределенными ("Некоторые слушатели БЮИ МВД РФ – отличники").

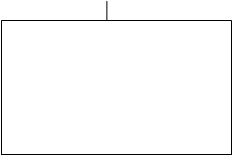
Особый случай простых суждений представляют так называемые выделяющие и исключающие суждения, так или иначе объединяющие в себе одновременно утверждение и отрицание. Выделяющими называются суждения, отображающие тот факт, что рассматриваемый признак принадлежит только данному предмету и не принадлежит всем прочим предметам этого рода. Исключающие суждения есть суждения, в которых сказуемое утверждает что-либо обо всех предметах за исключением известных определенных случаев.

Таким образом, суждения подразделяются по качеству (утвердительные и отрицательные) и по количеству (единичные, частные и общие).

Вместе с тем, суждения могут подразделяться по форме существования, – безусловные (категорические), условные и разделительные, – и по степени достоверности отношения к истине, – ассерторические (констатирующие), аподиктические (необходимо достоверные) и проблематические (вероятностные).

Примеры:

"Только те курсанты БЮИ МВД РФ, которые успешно освоили полный объем учебной дисциплины, имеют основания получить оценку "Отлично"(выделяющее суждение).

"Все первокурсники БЮИ МВД РФ, за исключением троих отсутствовавших, получили зачет по логике" (исключающее суждение).

"Все курсанты БЮИ МВД РФ изучают логику" (безусловное суждение).

"Тяжело в учении, легко – в бою" (А.В. Суворов) (условное суждение).

"Или пан, или пропал" (разделительное суждение).

"Каждый год БЮИ МВД РФ производит выпуск профессионально подготовленных специалистов для системы МВД" (ассерторическое суждение).

"Каждый солдат должен знать свой маневр" (А.В. Суворов)

(аподиктическое суждение).

"По-видимому, существует определенная зависимость между процессами социального реформирования общества и уровнем жизнеобеспечения населения" (проблематическое суждение).

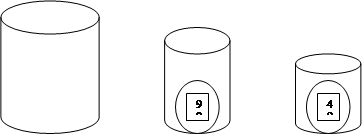
Учитывая, что в суждении могут быть только два качества и только два количества, можно легко прийти к заключению, что существуют только четыре вида атрибутивных суждений: общеутвердительные (обозначаются "A"), частноутвердительные (обозначаются "I"), общеотри­цательные (обозначаются "E") и частноотрицательные (обозначаются "O").

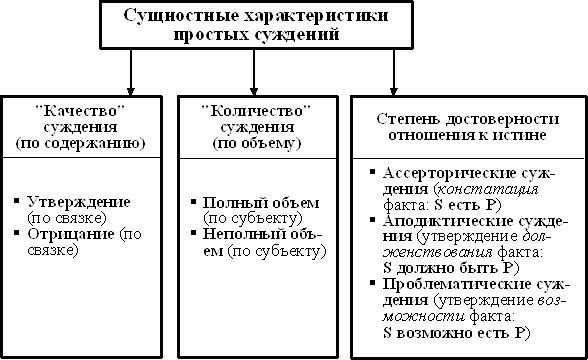
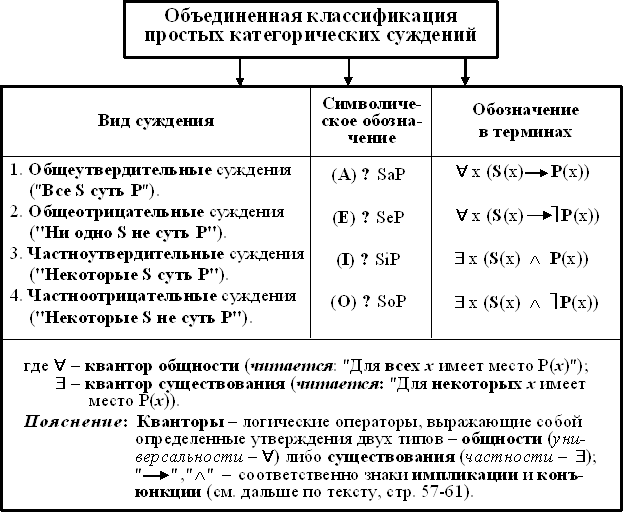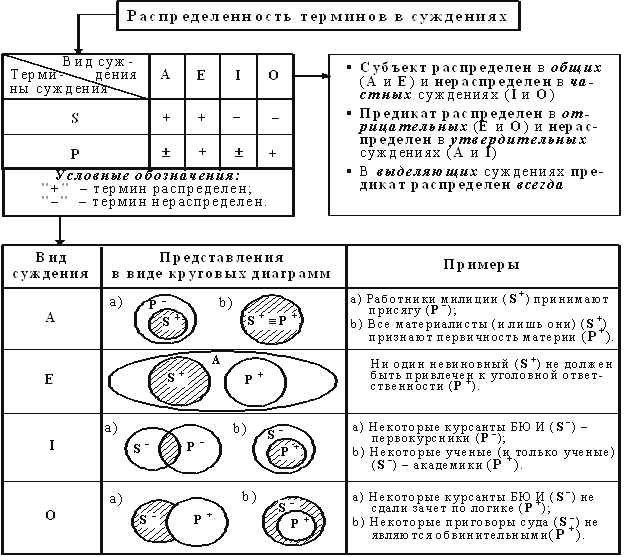
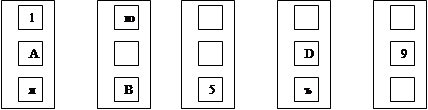
Применительно к суждениям надо учесть еще одну важную характе­ристику терминов суждения – субъекта и предиката: распределенность. Здесь термин считается распределенным, если он взят в полном объеме, и нераспределенным, если он взят не в полном объеме. Можно сказать, что субъект распределен в общих ("A" и "E") и не распределен в частных сужде­ниях ("I" и "O"). Предикат распределен в отрицательных ("Е" и "О") и не распределен в утвердительных суждениях ("A" и "I").
 

Примечание:

Происхождение символов "A", "I", "E" и "O" основано на следующем соглашении: "A" и "I" есть первые гласные буквы термина Affirmo (лат. "утверждаю"), а "E" и "O" – первые гласные буквы термина Nego (лат. "отрицаю").

Вопрос № 2. Сложные суждения и их виды. Методика анализа сложных суждений

До сих пор мы рассматривали только суждения, обра­зованные одним-единственным субъектом и одним-единственным предика­том. Такие суждения, как было сказано выше, называются простыми. Если же теперь связать между со­бой ряд простых суждений, то полученные в результате этого новые суждения будут уже сложными (сложенными). В логике сложные суждения подразделяют­ся на виды: соединительные, раздели­тельные, условные и эквивалентные.

Соединительные суждения иначе называются конъюнктивными (от лат. conjuncto - объединение). Соединение простых суждений друг с другом осуществляется здесь посредством союза "и". Однако в этом же смысле используются и другие выражения, например, "а", "но", "а также", "как и", "хотя", "однако", "несмотря на", "одновременно" и др. Записывается соединение двух суждений как p Ù q, что и на­зывается логической операцией "конъюнкция".

Пример:

Все люди рождаются свободными и равными в своем достоинстве и правах (Всеобщая декларация прав человека).

Нетрудно видеть, что в приведенном сложном суждении конъюнктивно объединены четыре простых суждения:

1)         Все люди рождаются свободными в своем достоинстве (p);

2)         Все люди рождаются свободными в своих правах (q);

3)         Все люди рождаются равными в своем достоинстве (r);

4)         Все люди рождаются равными в своих правах (t).

Таким образом, указанное сложное суждение с учетом выявленных простых суждений может быть записано в виде следующей формулы:

p Ù q Ù r Ù t.

Обратим внимание, что не всякое соединение суждений дает непременно истин­ный результат. В каком случае мы получаем истину (И), а в каком – ложь (Л), мы можем обнаружить на основании таблицы истинности конъюнктивных суждений:

"и" p "и" q		"то" (p Ù q)
И	И	И
И	л	Л
Л	и	л
Л	л	л

Образно отношение в конъюнктивном суж­дении можно выразить высказыванием: "В огороде бузина (p), в Киеве дядька (q)" (p Ù q).

Разделительные суждения иначе называются дизъюнктивными (от лат. disjunctio – разделяю). Разделение здесь осуществляется посредством союза "или". Записывается разделение как p Ú q, что и называется логи­ческой операцией "дизъюнкция". Дизъюнкция при этом бывает как строгая (сильная), так и нестрогая (слабая). Строгая дизъюнкция (записывается как p q) употребляется только в разделительном смысле. Члены строгой дизъюнкции называются в логике альтернативами.

Пример:

"Преступления могут быть либо неумышленными, либо умышленными".

Нетрудно видеть, что в приведенном сложном суждении дизъюнктивно связаны два простых суждения:

1)   Преступления могут быть неумышленными (p);

2)   Преступления могут быть умышленными (q).

Здесь две альтернативы.

Таким образом, указанное сложное суждение с учетом выявленных простых суждений может быть записано в виде следующей формулы:

p q.

Вновь обратим внимание, что не всякое строгое разделение суждений дает устойчиво истинный результат. Как это выглядит, видно из приведенной ниже таблицы:

"или" p "или" q		"то" (p q)
И	И	Л
И	л	И
Л	и	И
Л	л	л

Образно отношение в строгом дизъюнктивном суж­дении можно выразить высказыванием: "Или пан (p), или пропал (q)" (p q).

Нестрогая дизъюнкция (записывается как p Ú q) употребляется уже не в чисто разделительном, а в раз­делительно-соединительном смысле.

Пример:

"В уголовном праве ошибка может быть обозначена либо как фактическая, ли­бо как логическая".

Нетрудно видеть, что в приведенном сложном суждении дизъюнктивно объединены два простых суждения, что по отдельности дает три смысла:

1)   В уголовном праве ошибка может быть обозначена как фактическая (p);

2)   В уголовном праве ошибка может быть обозначена как логическая (q).

3)   В уголовном праве ошибка может быть обозначена как одновременно фактическая и логическая (p Ùq).

Таким образом, указанное сложное суждение с учетом выявленных простых суждений может быть записано в виде следующей формулы:

p Ú q.

Обратим внимание, что не всякое нестрогое разделение суждений дает устойчиво истинный результат. Как это выглядит, видно из приведенной ниже таблицы:

p "или" ("и") q		"то" (p Ú q)
И	И	И
И	л	И
Л	и	И
Л	л	л

Образно отношение в нестрогом дизъюнктивном суж­дении можно выразить высказыванием: "То ли дождик (p), то ли снег (q)" (p Ú q).

Обратите особое внимание на то, что нестрогая дизъюнкция на практике встречается гораздо чаще, чем строгая!!!

Перейдем к суждениям условного типа. Условные суждения иначе называются импликативными (от лат. implicatio – сплетение, переплетение). Само условие в суждениях записы­вается посредством союза "если, то...". Суждение, выражающее в условном суждении само условие, называется антецедентом, суждение же, выра­жающее в условном суждении лишь результат, – консеквентом. Связь между ан­тецедентом и консеквентом и есть импликация, что записывается как p → q, а читается так: "Если p, то q".

Пример:

"Лес рубят – щепки летят".

Перепишем приведенную пословицу в соответствующей логической форме: "(Если) лес рубят, (то) щепки летят".

Обратим внимание здесь на то, что союз "если..., то..." может быть и не выражен в явном виде, а обозначен только контекстуально.

Нетрудно видеть, что в приведенном сложном суждении импликативно объединены два простых суждения:

1)   Лес рубят (антецедент – p);

2)   Щепки летят (консеквент – q).

Таким образом, указанное сложное суждение с учетом выявленных простых суждений может быть записано в виде следующей формулы:

p → q.

Подобно конъюнкции и дизъюнкции, не всякая импликация сужде­ний дает истинный результат. Отношения истинности и ложности суждений при импликации можно увидеть из нижеприведенной таблицы истинности.

"если" p "то" q		"то" (p → q)
И	И	И
И	л	Л
Л	и	И
Л	л	И

Образно отношение в суждениях импликации можно выразить высказыванием: "Лес рубят (p) – щепки летят (q)" (p → q).

Заметим, что при импликации антецедент выполняет функцию основания сужде­ния, но только достаточного, а не необходимого, ибо и при ложном основа­нии могут быть истинные следствия!!!

Пример:

Рассмотрим высказывание: "Если использовать метод уголов­ных репрессий, то можно ликвидировать преступность".

Дей­ствительно, борьба с преступностью в этом случае может быть успеш­ной, однако сами по себе репрессии направлены все же не против самой преступности, а лишь против преступников. Так что ре­прессии все же "ликвидируют" не преступность, а преступников.

В условных суждениях союз "если..., то..." может быть заменен на другие союзы, выполняющие ту же функцию условия. Среди последних наибольшее распространение получили союзы "там..., где...", "тогда..., когда...", "поскольку..., постольку...", "при наличии..., следует...", "в случае..., следует...", "при условии..., наступает... " и др.

В завершении рассмотрения этого вопроса подчеркнем, что во всех случаях условного суждения связка "антецедент – консеквент" выполняет функцию логического следования.

И, наконец, рассмотрим эквивалентные суждения, которые иначе называются суждениями с двойной импликацией. Эквиваленция, или двойная имплика­ция, записывается посредством союза "если и только если..., то...". Символически это выглядит так: p ↔ q.

Пример:

"Если содержание понятия увеличивается, его объем умень­шается" (p); "Если объем понятия уменьшается, его содержание увеличивается" (q).

Таким образом, указанное сложное суждение с учетом выявленных простых суждений может быть записано в виде следующей формулы:

p ↔ q.

Таблица истинности при эквиваленции выглядит так:

"если и только если" p "то" q		"то" (p ↔ q)
И	И	И
И	л	Л
Л	и	Л
Л	л	И

Образно отношение в суждениях эквиваленции можно выразить высказыванием: "Если хочешь быть здоров (p) – закаляйся (q)" (p ↔ q).

Названные выше логические связки, на основе которых образуются сложные суждения, – конъюнкция (Ù), дизъюнкция (Ú, ), импликация (→) и эквиваленция (↔), – называются пропозициональными связками, или пропозициональными союзами (от лат. propositio – предложение).

 
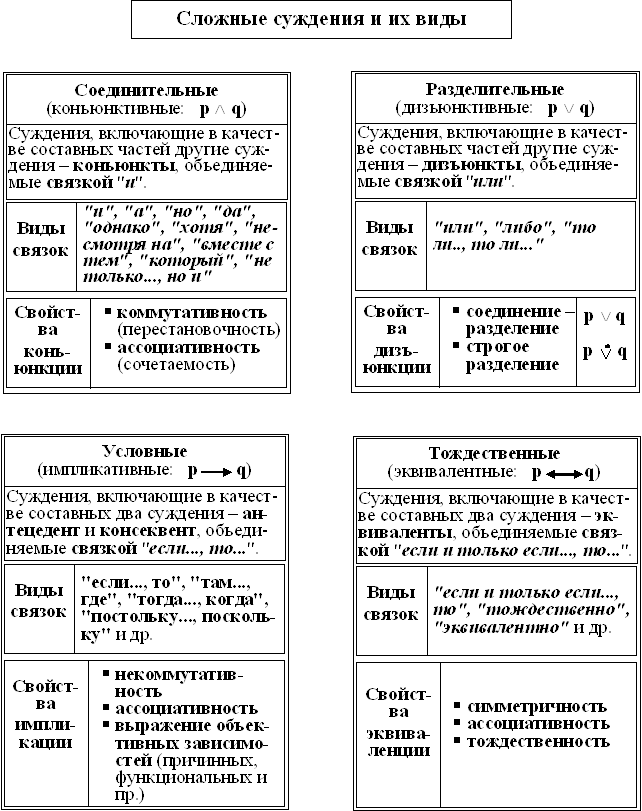
Важное практическое значение для сложных суждений имеет операция логического отрицания. В случае сложных суждений логическое отрицание может быть применено к конъюнкции, дизъюнкции и импликации.

Логическое отрицание конъюнктивного суждения может быть произведено на основе закона де Моргана. В результате мы получим логический закон дизъюнкции (нестрогая дизъюнкция):

ù (p Ù q) ↔ (ù p Ú ù q).

Пример:

Исходное суждение: "Все сотрудники ОВД России должны обладать высокими профессиональными и нравственными качествами".

Логическое отрицание: "Неверно, что все без исключения сотрудники ОВД России обладают высокими профессиональными и нравственными качествами" ↔ "Верно, что все без исключения сотрудники ОВД России не могут обладать высокими профессиональными или высокими нравственными качествами".

Логическое отрицание дизъюнктивного суждения (нестрогая дизъюнкция) производится также на основе закона де Моргана, в результате чего получаем логический закон конъюнктивного вида: ù (p Ú q) ↔ (ù p Ù ù q).

Пример:

Исходное высказывание: "Природа преступности, по-видимому, заложена либо в биологической, либо в социальной природе человека".

Логическое отрицание: "Неверно, что природа преступности заложена либо в биологической, либо в социальной природе человека" ↔ "Верно, что природа преступности заложена не в биологической и не в социальной природе человека".

Логическое отрицание импликативного суждения приводит к логическому закону следующего вида: ù (p → q) ↔ (p Ù ù q).

Пример:

Исходное высказывание: "Если сотрудник ОВД России имеет высшее образование, то он является классным специалистом".

Логическое отрицание: "Неверно, что если сотрудник ОВД России имеет высшее образование, то он является классным специалистом" ↔ "Верно, что если сотрудник ОВД России может иметь высшее образование и не быть классным специалистом".

Суждения, как и понятия, делятся на сравнимые (имеют общий субъект или предикат) и несравнимые (не имеют ничего общего). Сравнимые суждения в свою очередь делятся на совместимые и несовместимые.

Совместимые суждения выражают одну и ту же мысль полностью или в некоторой ее части. В логике рассматриваются следующие отношения совместимости суждений: эквивалентность, логическое подчинение, частичное совпадение (субконтрарность).

Пример:

1. "Юрий Гагарин – первый в мире космонавт" (эквивалентность);

2. "Кража, поскольку она является противоправным деянием, уголовно наказуема" (логическое подчинение);

3. "Не всякий генерал от природы полный" (Козьма Прутков) (частичное совпадение).

Наряду с отношениями совместимости, суждения вступают в отношения и несовместимости друг с другом. Два высказывания p и q называются несовместимыми, если из истинности одного из них необходимо следует ложность другого, т.е. p и q никогда не могут оказаться одновременно истинными.

Такими отношениями являются противоположность (контрарность) и противоречивость (контрадикторность).

Пример:

1. "Логическое определение любого качества через его противоположность является непродуктивным" (противоположность);

2. "Невозможно в одно и то же время находиться и не находиться в одном и том же месте" (противоречивость).

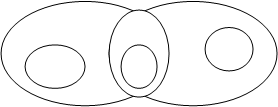
Совместимые и несовместимые отношения между двумя суждениями принято схематически изображать в виде так называемого "Логического квадрата":

Наряду с формами мышления формальная логика рассматривает в качестве своего предмета также и законы правильного мышления. Напомним, что традиционно под законами мышления понимаются необходимые, существенные, устойчивые, повторяющиеся связи между мыслями.

Наиболее фундаментальные связи между мыслями выступают здесь как основные формально-логические законы. К ним относятся законы: тождества, непротиворечия, исключенного третьего, достаточного основания.

Формально-логический закон тождества выступает как исходный принцип процесса правильного мышления, ибо соблюдение требований этого закона гарантирует определенность и ясность как основополагающие качества мышления. Сущностной характеристикой этого закона является тождественность развивающейся мысли. Иначе говоря, суть данного закона сводится к тому, чтобы в процессе определенного рассуждения всякие понятия и суждения оставались бы тождественными самим себе. Это требование к мышлению, выраженное законом тождества, выступает как нормативное правило (принцип) всякого правильного мышления.

Обратим внимание в этой связи на то, что понятие "тождественность" равносильно понятию "тожественность", т.е. понятию "быть тем же самым" (то же самое). Поэтому очевидно, что в точном смысле этого слова абсолютно тождественных объектов не бывает, и любой объект может быть абсолютно тождественным только самому себе, причем в одно и то же время и в одном и том же отношении!

Отсюда логика говорит лишь об относительном тождестве, т.е. о тождестве только определенных отношений между сходными объектами.

Закон тождества закладывает основы сохранения правильного мышления. Определяет же границы правильного мышления другой закон – закон непротиворечия, смысл которого сводится к тому, чтобы в процессе мышления не было взаимно исключающих друг друга мыслей. Это означает, что если закон тождества концентрирует внимание на принципе тождества развивающейся мысли, то закон непротиворечия – на принципе запрета противоречия в процессе этого развития.

Специфическими (особенными) проявлениями общих принципов логического мышления, – закона тождества и закона непротиворечия, – являются закон исключенного третьего и закон достаточного основания. Действительно, закон исключенного третьего вполне выводится по формальным основаниям (в соответствии с законом де Моргана) из закона непротиворечия:

[ ù (A Ù ù A) ] º [ ù A Ú ù (ù A) ] º [ ù A Ú A ] º [ A Ú ù A ].

Приведенная "логическая цепочка" свидетельствует о том, что закон исключенного третьего есть в действительности тот же самый закон непротиворечия, но который в данном случае проявляет себя при отсутствии "посредника" ("посредствующего звена"), связывающего "противоположности". Например, смысл и прочность семьи определяется наличием детей как "посредников".

Специфической же конкретизацией закона тождества выступает закон достаточного основания.

Особенностью проявления закона достаточного основания является то, что устойчивость мышления, в целом постулируемую законом тождества, закон достаточного основания переносит именно на сущностные (достаточные) основания, лежащие в основе любого конкретного процесса мышления.

Первые три из названных выше основных законов (принципов) формально-логического мышления, – закон тождества, закон непротиворечия и закон исключенного третьего, – сформулированы Аристотелем, закон (принцип) достаточного основания сформулирован Лейбницем.

Законы логики, – как основные, так и неосновные, – функционируют в мышлении в качестве принципов именно правильного рассуждения в ходе доказательства истинных и опровержения ложных высказываний. Последнее особенно важно, ибо из лжи, как это может показаться ни парадоксальным, логически могут следовать какие угодно высказывания, так как ложь фактически ни за какое логическое следование не отвечает.

Как было подчеркнуто выше, исходным в ряду формально-логических законов выступает закон тождества. Суть этого закона Аристотель выразил так: "Невозможно что-либо мыслить, если не мыслят что-то одно". Из закона тождества, таким образом, следуют два требования: