Навигация
Визначення показників зв’язку при прямій парній залежності
3.1 Визначення показників зв’язку при прямій парній залежності
Кореляційний аналіз – це метод кількісної оцінки взаємозв’язку між статистичними ознаками, що характеризують окремі соціально-економічні процеси.
Кореляційний зв'язок проявляється не в кожному окремому випадку соціально-економічних процесів, а при великій кількості спостережень та порівнянні середніх значень взаємопов’язаних ознак. Цей зв'язок існує на законі великих чисел, який реалізується в масовому процесі як тенденція до зростання або зниження результативної ознаки в залежності від відповідної зміни факторної ознаки.
З математичної точки зору кореляційна залежність – це функціональне співвідношення між середніми значеннями визначених ознак. За допомогою методу кореляційного аналізу вирішуються 2 основні задачі:
1.Визначення форми зв’язку
2.Вимірювання тісноти зв’язку
Перша задача вирішується знаходженням рівняння зв’язку і визначенням параметрів. Це рівняння регресії.
Друга – за допомогою розрахунку показників тісноти зв’язку (коефіцієнта кореляції, кореляційного відношення та ін.). Схематично кореляційний метод аналізу можна поділити на 5 етапів:
1. Визначення задачі, встановлення наявності зв’язку між вивчаємими ознаками.
2. Відбір найбільш суттєвих факторів для аналізу.
3. Визначення характеру зв’язку, його направлення і форму, підбір математичного рівняння для вираження існуючих зв’язків.
4. Розрахунок числових характеристик кореляційного зв’язку (визначення параметрів рівняння і показників тісноти зв’язку).
5. Статистична оцінка вибіркових показників зв’язку
В статистичних дослідженнях часто приходиться мати справу з прямолінійною формою зв’язку, котра виражається рівнянням прямої лінії
![]()
де: ![]() – вирівняне значення результативної ознаки,
– вирівняне значення результативної ознаки,
х – значення факторної ознаки,
а – початок відліку,
в – коефіцієнт регресії.
При вивченні кореляційного зв’язку виникає необхідність поряд з вирішенням рівнянь регресії вимірювати також ступінь тісноти зв’язку між ознаками. При парній лінійній залежності тіснота зв’язку визначається за допомогою лінійного коефіцієнта кореляції;
![]()
де: ![]() ,
, ![]() ,
, ![]()
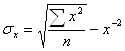 ,
, 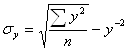
Коефіцієнт знаходиться в межах від - 0 до +,- 1. Якщо коефіцієнт кореляції дорівнює нулю, то зв’язок відсутній, якщо одиниці, то зв’язок функціональний. Знак + ,– біля коефіцієнта кореляції вказує на направлення зв’язку (+ - пряма, – обернена). Чим ближче коефіцієнт кореляції к одиниці, тим зв’язок між показниками тісніший. Квадрат коефіцієнта кореляції називається коефіцієнтом детермінації (г2). Він показує, яка частина сукупній варіації ознаки визначається вивчаємим фактором. Якщо коефіцієнт детермінації виражений у %, то його потрібно читати наступним чином: варіація залежної змінної на стільки то відсотків обумовлена варіацією фактора. При наявності криволінійної залежності тіснота зв’язку між ознаками визначається за допомогою кореляційного відношення:
h=![]()
де: ![]() – міжгрупова дисперсія
– міжгрупова дисперсія
![]() – загальна дисперсія
– загальна дисперсія
Кореляційне відношення знаходиться в інтервалі від 0 до 1 і може бути використано для вимірювання тісноти зв’язку довільної форми.
Використовуючи дані про урожайність цукрових буряків і її факторах проведемо регресійно-кореляційний аналіз зв’язку між двома ознаками – урожайністю та якістю ґрунту. Для характеристики цього зв’язку необхідно визначити: 1) форму зв’язку і математичне рівняння зв’язку, для чого побудуємо графік кореляційної залежності між урожайністю (у – результативна ознака) і якістю ґрунту (х – факторна ознака);
2) параметри рівняння регресії;
3) тісноту зв’язку (коефіцієнти кореляції і детермінації).
Для визначення форми зв’язку між урожайністю (у) і якістю ґрунту (х) побудуємо графік – кореляційне поле. На осі абсцис нанесемо значення факторної ознаки (незалежної змінної – якість ґрунту), а на осі ординат – результативної ознаки (залежної змінної - урожайності). Графік показує, що зв’язок в даному випадку близький до прямолінійного і його можна виразити рівнянням прямої.
![]()
Ця лінія показує зміну урожайності під впливом якості ґрунту при виключенні випадкових відхилень ознаки. Параметри рівняння прямої а і б знайдемо із системи нормальних рівнянь:
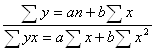
Всі необхідні дані для вирішення системи запишемо у таблицю 15.
Таблиця 15. Дані для розрахунку показників кореляційного зв'язку Отримані дані підставимо в систему рівнянь| № п/п | Урожайність, ц/га У | Якість ґрунту, балівх | Розрахункові величини | |||
| Ух | у2 | х2 | Очікуване значення урожайності | |||
| 1. | 142,4 | 50 | 7120 | 20277,8 | 2500 | 109,6 |
| 2. | 54,7 | 54 | 2953,8 | 2992,1 | 2916 | 119,9 |
| 3. | 57,2 | 40 | 2288 | 3271,8 | 1600 | 83,7 |
| 4. | 129,4 | 43 | 5564,2 | 16744,4 | 1849 | 91,5 |
| 5. | 125,3 | 61 | 7643,3 | 15700,1 | 3721 | 138,1 |
| 6. | 184,2 | 46 | 4347 | 8930,3 | 2116 | 99,2 |
| 7. | 94,5 | 56 | 10315,2 | 33929,6 | 3136 | 125,2 |
| 8. | 112,1 | 53 | 5941,3 | 12566,4 | 2809 | 117,4 |
| 9. | 171,2 | 63 | 10785,6 | 29309,4 | 3969 | 143,3 |
| 10. | 225,1 | 67 | 15081,7 | 50670 | 4489 | 153,7 |
| 11. | 97,9 | 58 | 5979,8 | 10629,6 | 3364 | 130,3 |
| 12. | 103,1 | 42 | 4111,8 | 9584,4 | 1764 | 88,7 |
| 13. | 127,6 | 62 | 7911,2 | 16281,8 | 3844 | 140,7 |
| 14. | 43,7 | 63 | 2753,1 | 1909,7 | 3969 | 143,3 |
| 15. | 135,1 | 65 | 8807,5 | 18360,3 | 4225 | 148,5 |
| 16. | 162,8 | 53 | 8628,4 | 26503,8 | 2809 | 117,4 |
| 17. | 203,1 | 56 | 11373,6 | 41249,6 | 3136 | 125,2 |
| 18. | 78,8 | 53 | 4176,4 | 6009,4 | 2809 | 117,4 |
| 19. | 95,8 | 53 | 5077,4 | 9177,6 | 2809 | 117,4 |
| 20. | 68,4 | 46 | 3146,4 | 4678,6 | 2116 | 99,2 |
| 21. | 151,5 | 60 | 9090 | 22952,3 | 3600 | 135,5 |
| 22. | 108,1 | 66 | 7134,6 | 11685,6 | 4356 | 151,1 |
| 23. | 93,2 | 59 | 5498,8 | 8686,2 | 3481 | 132,9 |
| 24. | 118,5 | 52 | 6162 | 14042,3 | 2704 | 114,8 |
| 25. | 200,6 | 62 | 12437,2 | 40240,4 | 3844 | 140,7 |
| Разом | 3084,7 | 1383 | 174328,3 | 436383,5 | 77935 | 3084,7 |
| В середньому | 137 | 55,3 | 6973,1 | 17455,3 | 3117,4 | 123,38 |
174328,3=1383а+77935b 1383
Поділимо рівняння на коефіцієнт при а: 123,38=а+55,32b126,05=a+56,35b
Візьмемо перше рівняння із другого:
2,67=1,03b
Звідси: ![]() ц/га на 1 бал
ц/га на 1 бал
Підставивши значення b в І рівняння, знайдемо а:
123,38=а+55,32b123,38=а+55,32*2,59
![]() ц/га
ц/га
Рівняння регресії, яке виражає зв’язок між урожайністю та якістю ґрунту, матиме вигляд:
![]()
Коефіцієнт регресії b=2,59 показує, що з підвищенням якості ґрунту на 1 бал урожайність зернових культур у середньому для даної сукупності ТОВ зростає на 2,59 ц/га.
Перевіримо правильність розрахунків системи, виходячи із рівності:
123,38=– 19,89+2,59*55,32 ; 123,38 = 123,38
За рівнянням регресії можна визначити очікувані значення урожайності при різних значеннях якості ґрунту. Для цього замість х підставимо його конкретні значення:
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
![]() ц/га
ц/га
Усі обчислені дані запишемо в останню графу таблиці 15
Перевіримо правильність усіх розрахунків, зіставивши суми фактичної і розрахункової урожайності:
![]() ; 3084,7=3084,7
; 3084,7=3084,7
Визначимо тісноту зв’язку між досліджуваними ознаками (урожайністю та якістю ґрунту).
![]() ;
; ![]() ;
; ![]()
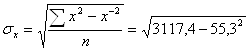 =59,31=7,70
=59,31=7,70
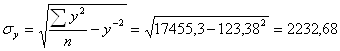 =47,2
=47,2
![]()
Коефіцієнт кореляції можна розрахувати і за іншою формулою:
![]()
Нами визначений коефіцієнт кореляції показує, що між собівартістю і урожайністю існує обернений зв’язок, тому що r рівний від’ємному значенню. Також він показує, що даний зв’язок є слабким.
Коефіцієнт детермінації r² = 0,0051 показує, що 0,51% загальних коливань урожайності обумовлено якістю ґрунту, а інша частина загальних коливань собівартості зумовлена іншими факторами, які в даному випадку не були враховані.
На основі таблиці 15 можемо побудувати кореляційне поле залежності урожайності цукрових буряків від якості ґрунту та теоретичну лінію регресії (рис.4).
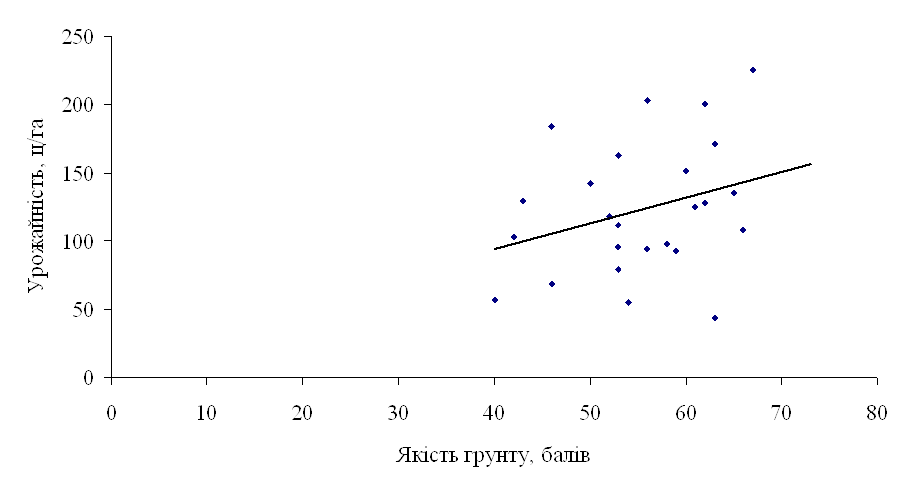
Рис 4. Кореляційне поле залежності урожайності цукрових буряків від якості ґрунту
Розділ IV. Динаміка та прогнозування урожайності цукрових буряків
0 комментариев