Анализ динамики и структуры посевных площадей и урожайности зерновых культур

3. Анализ динамики и структуры посевных площадей и урожайности зерновых культур

Далее мы проведем анализ динамики и структуры посевных площадей и урожайности зерновых культур, что является одной из основных задач статистики. Он заключается в изучении процесса изменения социально-экономических явлений во времени, поскольку все явления находятся в непрерывном развитии. Показатели рядов динамики могут быть рассчитаны цепным и базисным методами. Базисный способ заключается в том, что каждый последующий (отчетный) уровень сопоставляется с одним постоянным уровнем, принятым за базу сравнения, обычно – первым приведенным периодом.

При цепном способе каждый последующий уровень сопоставляется со смежным (предыдущим) т.е. база берется не постоянная, а переменная.

Изучение уровня развития производства осуществляется путем вычисления следующих показателей: абсолютного прироста, темпов роста, темпов прироста, и значение 1 % прироста. Кроме того, для всего ряда динамики рассчитывается среднегодовой абсолютный прирост, среднегодовой темп роста.

1. Абсолютные приросты вычисляются как разность между каждым последующим уровнем и базой сравнения.

Базисный:  Цепной:

Y_i – Y₀  Y_i – Y_i-1

2. Темпы роста исчисляются как отношение последующего уровня динамики к базе сравнения и выражающегося в процентах.

Базисный: Цепной:

(Y_i/Y_o)*100% (Y_i/Y_i-1)*100%

3. Темп прироста есть отношение соответствующего абсолютного прироста к первому или предыдущему уровню динамики, выраженное в процентах.

Базисный: Цепной:

(A/Y_o)*100% (A/Y_i-1)*100%

Или по формуле: Тпр – Тр*100%.

4. Абсолютное значение одного процента прироста можно получить как частное от деления абсолютного прироста на темп прироста:

Апр/Тпр.

5. В целях обобщения интенсивности развития изучаемого явления за весь период, рассчитывается для всего ряда динамики среднегодовой коэффициент или темп роста по формуле:

Тр=

Под корнем дано произведение цепных темпов роста в коэффициентах, а степень корня равна числу сомножителей под корнем.

Если неизвестны коэффициенты роста, а известны уровни, то среднегодовой темп роста можно рассчитать по формуле:

Тр=,

где У₁ и У_п – уровни первого и последнего периодов, а и в степени корня равно количеству лет, включая пропущенные.

6. Среднегодовой абсолютный прирост равен частному от деления суммы всех цепных абсолютных приростов на их число:

Апр=,

где n – число слагаемых в числителе.

Эта величина может быть также рассчитана по формуле:

Апр=,

где n – число уровней, включая пропущенные;

У_о  – уровень первого периода.

Все вычисления мы производили исходя из данных, представленных в таблице 3. №9.

Таки образом анализ скорости и интенсивности увеличения или уменьшения площади, используемой для посева сельскохозяйственных культур во времени осуществляется с помощью статистических показателей, которые получаются в результате сравнения уровней между собой. К таким показателям относятся, как уже было сказано выше: абсолютный прирост, темп роста и прироста, абсолютное значение 1% прироста. В нашем случае базисом (уровень с которым происходит сравнение) является 2000 г.

 Таким образом, анализируя полученные данные можно сказать, что по отношению к предыдущему периоду площадь с/х угодий в 2001 г. на 10 га меньше, чем в 2000 г., в 2002 г на 311 га больше, чем в 2001 г; в 2003 г. площадь меньше на 511 га, чем в 2002 г.; в 2004 г. площадь больше на 658 га, чем в 2003 г. и в 2005 г. площадь меньше на 369 га, чем в 2004 г. Так в 2004 г. самая большая площадь посева, а в 2003 г. самая маленькая, по сравнению со всеми остальными анализируемыми годами.

По отношению же к базисному периоду (2000 г.) в 2001г. площадь меньше на 10 га; 2002г. больше на 301 га; 2003г. на 210 га меньше; 2004г. на 448 га больше, и в 2005г. на 79 га больше, чем посеянная в базисном году. В итоге площадь с/х угодий в 2005 году в целом увеличилась на 79 га по сравнению с базисом.

Формой выражения интенсивности изменения уровня являются коэффициент роста и темп роста. Коэффициент роста показывает, во сколько раз данный уровень больше базисного (если он больше единицы) или какую часть базисного уровня составляет уровень текущего периода за некоторый промежуток времени (если он меньше единицы). Так 2002г. в 1,67 раз; 2004г. в 3,52 раза больше 2000 года. А 2001 г. составляет 0,98 часть, 2003 г. 0,34 часть и 2005 г. 0,60 часть базисного периода.

Таким образом, видно, что увеличение и уменьшение посевных площадей неравномерно чередуются от года к году.

	Показатели динамики посевных площадей под зерновыми и зернобобовыми культурами за последние 6 лет в ГУП ОПХ "Орошаемое"
								Таблица 3. №9
№ п/п	Годы	Площадь, га	Абсолютный прирост, га		Темп роста, % Коэффициент роста		Темп прироста, %		Абсолютное значение 1% прироста (только по цепному).
			цепной	базисный	цепной	базисный	цепной	базисный
1	2	3	4	5	6	7	8	9	10
1	2000	471	-	-	-	-	-	-	-
2	2001	461	-10	-10	98	98	-2	-2	4,71
3	2002	772	311	301	167	164	67	64	4,61
4	2003	261	-511	-210	34	55	-66	-45	7,72
5	2004	919	658	448	352	195	252	95	2,61
6	2005	550	-369	79	60	117	-40	17	9,19
ИТОГО:		3 434	79	608	711	629	211	129	28,84
Среднегодовой темп роста Т роста =				1,005*100%=100,5%
Среднегодовой темп прироста Т прироста =				100,5-100%= 0,5%
Абсолютный среднегодовой прирост А прирост =				15,8
Абсолютный среднегодовой прирост через уровни А прирост =						15,8

Относительную скорость изменения уровня ряда в единицу времени характеризует темп прироста.

Темп прироста показывает, на какой процент уровень данного периода или момента времени больше (или меньше) базисного уровня. Так 2001 и 2003гг. меньше базисного на -2% и -45% соответственно, а 2002, 2004 и 2005 ггг. больше на 64%, 95% и 17% соответственно.

Абсолютное значение 1% прироста представляет собой сотую часть базисного уровня и в то же время – отношение абсолютного прироста к соответствующему темпу роста. Он показывает, сколько физических единиц приходится на 1% прироста. Так большинство физических единиц 9,19 приходится на 1% прироста в 2005 году, меньшинство – в 2004 году – 2,61.

Обобщающим показателем скорости изменения площади посевов во времени является среднегодовой абсолютный темп прироста. Этот показатель дает возможность установить, насколько в среднем за единицу времени должен увеличиваться уровень ряда (в абсолютном выражении), чтобы, отправляясь от начального уровня за данное число периодов (лет), достигнуть конечного уровня. В нашем случае он составляет 15,8, следовательно, в этом исчислении должен увеличиваться уровень ряда за 1 год, чтобы достигнуть конечного уровня.

Обобщающей характеристикой интенсивности изменения уровней ряда динамики служит среднегодовой темп роста, показывающий во сколько раз в среднем за единицу времени изменился уровень динамического ряда. Таким образом, у нас он изменился в 100,5 раз.

Среднегодовой же темп прироста в нашем случае увеличился лишь на 0,5%.

Одним из методов анализа и обобщения динамических рядов является выявление его основной тенденции или сокращению Тренда.

Т.е. влияние эволюционного характера – это изменения, определяющие некое общее направление развития, как бы многолетнюю эволюцию, которая пробивает себе дорогу через другие систематические и случайные колебания. Такие изменения динамического ряда называются тенденцией развития или трендом.

Тренд – это долговременная компонента ряда динамики. Она характеризует основную тенденцию его развития, при этом остальные компоненты рассматриваются только как мешающие процедуре его определения.

После того как установлено наличие тенденции в ряду динамики, производится ее описание с помощью методов сглаживания.

В статистической практике выявление основной тенденции развития производится тремя способами (т.е. методами сглаживания):

– способом скользящей средней;

– способом наименьших квадратов;

– выравниванием по среднегодовому абсолютному приросту.

Выравнивание по среднегодовому абсолютному приросту исчисляется по формуле:

У_п  = У₁+Аср*п,

где Аср – среднегодовой абсолютный прирост;

п – порядковый номер уровня.

Наиболее эффективным способом выявления тенденции является аналитическое выравнивание (способ наименьших квадратов) по прямой, параболе 2-го порядка или гиперболе. Выравнивание по прямой имеет выражение:

У_t= a+в_t,

где t – условное обозначение времени, т.е. порядковый номер года;

а и в – параметры уравнения.

Цифровое уравнение параметров уравнения прямой находится в результате решения системы уравнений:

∑У=nа+в∑t,

∑ Уt=а∑ t+ в∑t²,

где у – фактические уровни, за 10-летний период времени;

n – число членов ряда (число лет);

t – порядковый номер года.

Исследование динамики социально-экономических явлений и выявление их основных черт в прошлом дают основания для экстраполяции – определения бедующих размеров уровня экономического явления. Экстраполяцию можно использовать для прогнозирования показателей, при обобщении выводов и предложений.

Чаще всего экстраполяцию связывают с аналитическим выравниванием тренда. При этом для определения уровня в любом бедующем году, для которого найдена зависимость от времени, достаточно подставить порядковый номер года в аналитическое уравнение и определить уровень на перспективу (таблица 3. №10).

104=8а+36в,

510=36а+204в.

а=

36*(,

4,5(104-36в)+204в=510,

468-162в+204в=510,

42в=510-468,

42в=42/42,

в=1.

а=

Следовательно, уравнение прямой будет иметь следующий вид:

У_t= 8,5+1_t,

	Выявление тенденции за 8 последних лет в ГУП ОПХ "Орошаемое"
Анализ урожайности зерновых культур, в том числе озимых и яровых в динамике за 8 -10 лет
									Таблица 3. №10.
	Годы	Порядковый номер года, t		Уровни ряда, у		Расчетные величины				Теоретическое значение уравнений уt=a+вt			(Уi-Уср)2		(Уt-Уt)2
						t2		уt
	1	2		3		4		5		6			7		8
	1998	1		8,1		1		8		9,50			24,01		1,96
	1999	2		8,5		4		17		10,50			20,25		4,00
	2000	3		12,6		9		38		11,50			0,16		-12,44
	2001	4		18,6		16		74		12,50			31,36		37,21
	2002	5		11,5		25		58		13,50			2,25		4,00
	2003	6		14,2		36		85		14,50			1,44		0,09
	2004	7		14,4		49		101		15,50			1,96		1,21
	2005	8		16,1		64		129		16,50			9,61		0,16
	-	9
	-	10
	ИТОГО:		36		104,0		204		510		104,00	91,04		36,19

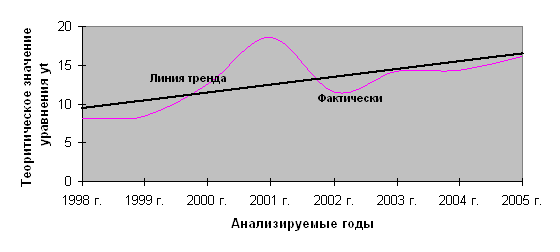
рис. 3. №2

По графику (рис. 3. №2) видно, что развитие ряда стремится к возрастанию.

В таблице приведен ряд динамики за 8 последних лет, по которому найдено уравнение прямой линии, выражающий тренд: уt=a+вt. Данный ряд ограничен последним годом, для которого t=8. Для следующего года t=9, тогда уровень будет равен уt=a+в₉. Это можно использовать для прогноза урожайности в бедующие года.

Параметр «а» (в нашем случае он равен 8,5) трактуется как характеристика средних условий ряда динамики, параметр «в» – изменение ускорения (в нашем случае он равен 1).

Для характеристики влияния факторов на динамику урожайности определяют общую, случайную и факторную дисперсии.

=11,38; =3,37.

=4,524; _случ==2,13.

=6,856; =2,62.

Тогда коэффициент детерминации равен:

К_детер.==6,856/11,38=0,603.

Коэффициент случайной дисперсии равен:

=4,524/11,38=0,397.

Полученные результаты означают, что динамика урожайности в изучаемом периоде на 39,7% объяснялась влиянием различных признаков. От фактора признака (в данном случае фактор времени ассоциируется с влиянием научно-технического прогресса в сельском хозяйстве, улучшением технологии и повышением культуры производства) зависит 60,3% колебания урожайности.