Грузооборот отдельных видов транспорта общего пользования в РФ (в процентах к грузообороту ж/д транспорта) представлен в табл. 3.1

1. Грузооборот отдельных видов транспорта общего пользования в РФ (в процентах к грузообороту ж/д транспорта) представлен в табл. 3.1.

Таблица 3.1

Виды транспорта	Грузооборот, %
ж/д	100,0
морской	23,12
речной	8,75
трубопроводный	24,11
автомобильный	10,76
воздушный	0,08

Определите удельный вес видов транспорта в грузообороте и постройте секторную структурную диаграмму.

Какие относительные величины приведены в условии задачи? Какие относительные величины вы вычислили?

2. Промышленное предприятие перевыполнило план по валовой продукции на 4,3%. Увеличение объема выпуска валовой продукции предприятия по сравнению с прошлым годом составило 8,4%.

Определите плановую динамику по росту валовой продукции на этом предприятии.

3. Укажите относительные величины динамики:

а) производство чугуна увеличилось по сравнению с прошлым годом на 3 млн. т;

б) производство синтетических смол и пластмасс увеличилось по сравнению с прошлым годом в 1,1 раза.

Решение:

1) Определим суммарный грузооборот по отношению к грузообороту железнодорожного транспорта по всем элементам и найдем долю каждого элемента в общем грузообороте.

Таблица 3.2 Расчет структуры грузооборота

№ п/п	Виды транспорта	Грузооборот в % к грузообороту ж/д транспорта	Доля в общем грузообороте, %
1	ж/д	100	59,94
2	морской	23,12	13,86
3	речной	8,75	5,25
4	трубопроводный	24,11	14,45
5	автомобильный	10,76	6,45
6	воздушный	0,08	0,05
	Итого грузооборот:	166,82	100

Построим секторную диаграмму:

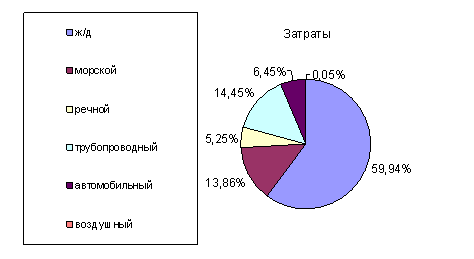
Рис. 3.1. Структура грузооборота по видам транспорта.

В таблице 3.1 приведены относительные величины сравнения. Т.е. грузооборот по какому-то виду транспорта сравнивался с грузооборотом по железнодорожному транспорту.

В таблице 3.2 рассчитаны относительные показатели структуры. Они характеризуют долю, которую каждый транспорт составлял в общем грузообороте.

2) Относительная величина выполнения плана – отношение фактического значения показателя к плановому его значению выраженное в процентах.

Для валовой продукции эта формула выглядит так:

%Вып. плана _ВП = ВП_факт / ВП_план * 100%

Соответственно процент перевыполнения плана будет равен:

Перевыполнение плана _ВП % = (ВП_факт – ВП_план) / ВП_план * 100%

Индекс выполнения планового задания равен:

I_ВПЗ = ВП_факт / ВП_план = Перевыполнение плана _ВП %/ 100 % + 1

I_ВПЗ = 4,3 / 100 + 1 = 1,043

Процент прироста валовой продукции характеризуется формулой:

Прирост _ВП = (ВП_факт – ВП_баз) / ВП_баз * 100%

Индекс роста валовой продукции равен:

I_ВП = ВП_факт / ВП_баз = Пррирост_ВП %/ 100 % + 1

I_ВП = 8,4 / 100 + 1 = 1,084

Плановый прирост валовой продукции определяется по формуле:

Прирост _{ВП план} = (ВП_план – ВП_баз) / ВП_баз * 100%

Индекс планового задания равен:

I_ПЗ = ВП_план / ВП_баз = Прирост _{ВП план} %/ 100 % + 1

Три перечисленных индекса связаны соотношением:

I_ВП = ВП_факт / ВП_баз = (ВП_факт / ВП_план) * (ВП_план / ВП_баз) = I_ВПЗ * I_ПЗ

Найдем индекс планового задания:

I_ПЗ = I_ВП / I_ВПЗ = 1,084 / 1,043 = 1,0393

Т.е. плановое задание составляло 103,93 % от базисного значения выпуска валовой продукции.

Прирост выпуска планировался на уровне 3,93%.

3) Укажите относительные величины динамики:

а) производство чугуна увеличилось по сравнению с прошлым годом на 3 млн. т;

Этот показатель называется абсолютным приростом.

б) производство синтетических смол и пластмасс увеличилось по сравнению с прошлым годом в 1,1 раза.

Этот показатель называется индексом (коэффициентом) роста.

Практическая работа №4

По трем районам города имеются следующие данные на конец года (табл. 4.1).

Таблица 4.1

Район города	Сумма вкладов в сбер. кассы, млн. руб.	Средний размер вклада, тыс. руб.	Среднее число вкладов на 1 сбер. кассу
1	5400	600	1500
2	3900	650	1000
3	8000	800	2000

Определить:

а) средний размер вклада;

б) среднее число вкладов в сберкассы;

в) среднее число сберкасс на 1 район города;

г) среднюю сумму вкладов.

Решение:

Средний размер вклада () находиться как отношение суммы вкладов (S_сумм) к числу вкладов (n).

Средний размер вклада по трем районам найдем по формуле средней геометрической взвешенной. Весом в данном случае будет выступать сумма вкладов.

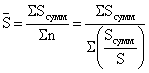
 = (5400 + 3900 + 8000) / (5400 / 600 + 3900 / 650 + 8000 / 800) =

= 17300 / (9 + 6 + 10) = 17300 / 25 = 692 тыс. руб.

Среднее число вкладов в сберкассы по всем районам города найдем как среднее арифметическое из числа вкладов в каждом районе:

 = 25 / 3 = 8,333 тыс. шт.

Зная число вкладов в каждом районе города (n) и среднее число вкладов на одну сберкассу (n_ед) можем найти число сберкасс (N):

N = n / n_ед

Найдем для каждого района города:

N₁ = 9000 / 1500 = 6 сберкасс

N₂ = 6000 / 1000 = 6 сберкасс

N₃ = 10000 / 2000 = 5 сберкасс

Найдем среднее число сберкасс в районе по формуле среднего арифметического:

 = (6 + 6 + 5) / 3 = 5,667 сберкасс.

Средняя сумма вкладов на район города находиться по формуле средней арифметической:

 = (5400 + 3900 + 8000) / 3 = 5766,667 млн. руб.

Средняя сумма вкладов на одну сберкассу находиться по формуле:

 = (5400 + 3900 + 8000) / (6 + 6 + 5) = 1017,647 тыс. руб.

Практическая работа №5

В соответствии с макетом по данным табл. 2.1 постройте группировку предприятий по признакам: X – объем продукции, Y – производительность труда.

Вычислите общую, внутригрупповые и межгрупповую дисперсии производительности труда; среднюю из внутригрупповых. Проверьте сложением дисперсий правильность Ваших расчетов.

Вычислите коэффициент детерминации.

Сделайте краткие выводы.

Решение:

Рассчитаем производительность труда для каждого завода.

Таблица 5.1

Заводы, п/п	Годовой объем продукции, млн. руб.	Производительность труда, тыс. руб. / чел.
1	1,7	6,07
2	4,8	10,00
3	3,7	8,81
4	6,1	12,08
5	9,4	13,24
6	9,6	9,41
7	2,1	4,29
8	2,6	5,20
9	4,5	7,26
10	8,4	8,48
11	9,7	10,43
12	2,3	5,35
13	3,4	6,07
14	6,3	10,33
15	9,8	10,83
16	7,3	9,86
17	1,8	4,62
18	2,6	6,05
19	4,8	9,41
20	16,1	12,88
21	1,3	3,82
22	2,3	5,90
23	1,3	5,20
24	3,4	6,94
25	5,6	12,87
26	2,2	8,46
27	1,9	8,44
28	6,1	8,65
29	8,2	13,23
30	3,6	11,61
31	4,6	11,22
32	2,5	10,64
Заводы, п/п	Годовой объем продукции, млн. руб.	Производительность труда, тыс. руб. / чел.
33	3,4	8,61
34	6,4	16,20
35	2,3	6,57
36	1,8	9,00
ИТОГО:	173,9	318,0

Разделим выборку на 5 классов. Величины интервалов определим из формул:

 , .

 , .

Составим корреляционную таблицу

Таблица 5.2

y			х
			3,82	6,30	6,30	8,78	8,78	11,25	11,25	13,73	13,73	16,20	Итого
1,30	4,26	10			5		3		1		0		19	2,78
4,26	7,22	0			2		4		2		1		9	5,74
7,22	10,18	0			1		4		2		0		7	8,70
10,18	13,14	0			0		0		0		0		0	11,66
13,14	16,10	0			0		0		1		0		1	14,62
Итого		10			8		11		6		1		36	-
		5,06			7,54		10,01		12,49		14,96		-	-

Значения в строке  и столбце  задают последовательность точек, которая иллюстрирует зависимость среднего значения результативного признака (у) от факторного признака (х) – эмпирическую линию регрессии.

Общая и межгрупповая дисперсии находятся по формулам :

 

где  - межгрупповая дисперсия;  - общая дисперсия.  - групповые средние;  - общая средняя; n_i - частота i-ой группы; y_i – i-й вариант признака; f_i – частота i-го варианта.

Общая дисперсия показывает вариацию результативного признака под воздействием всех факторов. Межгрупповая дисперсия показывает вариацию результативного признака, обусловленную вариацией группировочного. Средняя из внутригрупповых показывает вариацию результативного признака под воздействием факторов неучтенных при группировке. Средняя из внутригрупповых находиться по формуле средневзвешенной.

Все три вида дисперсий связаны правилом сложения трех дисперсий

 = +

Таблица 5.3 Вспомогательные расчеты для расчета межгрупповой дисперсии

Группа	ni	i	i –	(i – )2	ni · (i – )2
1	19	6,93	-1,91	3,63	69,00
2	9	10,89	2,06	4,23	38,09
3	7	10,78	1,95	3,80	26,60
4	0	0,00	-8,83	78,05	0,00
5	1	12,88	4,05	16,37	16,37
Итого	36	-	-	-	150,06

 = 150,06 / 36 = 4,168

Таблица 5.4 Вспомогательные расчеты для расчета общей дисперсии

Группа	ni	yi	yi –	(yi – )2	ni · (yi – )2
1	19	5,06	-3,8	14,2	270,5
2	9	7,54	-1,3	1,7	15,1
3	7	10,01	1,2	1,4	9,7
4	0	12,49	3,7	13,4	0,0
5	1	14,96	6,1	37,6	37,6
Итого	36	-	-	-	310,25

 = 310,25 / 36 = 8,864

Найдем внутригрупповую дисперсию по первой группе

Таблица 5.5 Расчетная таблица для расчета дисперсии по первой группе

№ п/п	y	y –	(y – )2
1	6,07	-0,86	0,735
2	8,81	1,88	3,538
3	4,29	-2,64	6,985
4	5,20	-1,73	2,988
5	5,35	-1,58	2,496
6	6,07	-0,86	0,735
7	4,62	-2,31	5,351
8	6,05	-0,88	0,778
9	3,82	-3,11	9,642
10	5,90	-1,03	1,063
11	5,20	-1,73	2,988
12	6,94	0,01	0,000
13	8,46	1,53	2,350
14	8,44	1,52	2,298
15	11,61	4,68	21,942
16	10,64	3,71	13,761
17	8,61	1,68	2,819
18	6,57	-0,36	0,128
19	9,00	2,07	4,290
Сумма	-	-	84,887

 = 84,887 / 19 = 4,468

Найдем внутригрупповую дисперсию по второй группе

Таблица 5.6 Расчетная таблица для расчета дисперсии по второй группе

№ п/п	y	y –	(y – )2
1	10,00	-0,50	0,245
2	12,08	1,58	2,509
3	7,26	-3,24	10,480
4	10,33	-0,17	0,028
5	9,41	-1,08	1,174
6	12,87	2,38	5,656
7	8,65	-1,84	3,396
8	11,22	0,72	0,524
9	16,20	5,71	32,572
Сумма	-	-	56,584

 = 56,584 / 9 = 7,073

Найдем внутригрупповую дисперсию по третьей группе

Таблица 5.7 Расчетная таблица для расчета дисперсии по третьей группе

№ п/п	y	y –	(y – )2
1	13,24	2,46	6,031
2	9,41	-1,37	1,882
3	8,48	-2,30	5,284
4	10,43	-0,35	0,125
5	10,83	0,05	0,002
6	9,86	-0,92	0,844
7	13,23	2,44	5,964
Сумма	-	-	20,133

 = 20,133 / 7 = 1,83

Внутригрупповая дисперсия по четвертой группе будет равна нулю, т.к. в этой группе нет ни одного завода.

 = 0

 Внутригрупповая дисперсия по пятой группе будет равна нулю, т.к. в этой группе только один завод.

 = 0

Найдем среднюю из внутригрупповых :

= (4,468 * 19 + 7,073 * 9 + 1,83 * 7 + 0 * 0 + 0 * 1) / 36 = 161,359 / 36 = 4,482

Проверим правило сложения дисперсий

 + =

4,168 + 4,482 = 8,865

 = 8,864

Т.е. правило сложения дисперсий выполняется.

Эмпирический коэффициент детерминации равен :

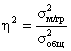
η² = 4,168 / 8,864 = 0,47

Т.е. 47 % вариации результативного признака объясняется вариацией факторного признака.

 

Практическая работа №6

На основе данных табл. 5.1 об объемах продукции () и расчетов показателей производительности труда  выполните следующие операции по расчету линии регрессии :

- нанесите данные объемов производства и производительности труда на корреляционное поле;

- сделайте вывод о возможной форме связи между объемом продукции и производительностью труда;

- для выбранной формулы с помощью метода наименьших квадратов рассчитайте величины коэффициентов;

- нанесите на график корреляционного поля уравнение регрессии;

- рассчитайте для данной формы связи необходимые показатели, характеризующие тесноту связи производительности труда с объемами продукции.

Решение:

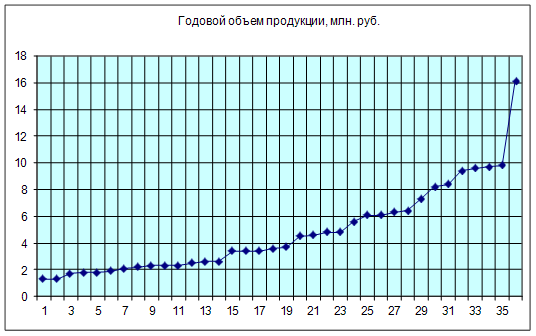
Построим корреляционное поле

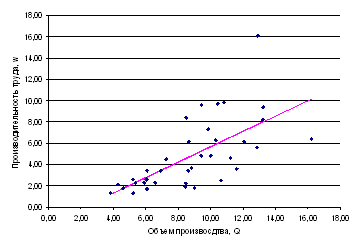
По графику можно предположить линейный характер связи между объемом производства (х) и производительности труда (у).

Рассчитаем параметры уравнения линейной парной регрессии.

Для расчета параметров a и b уравнения линейной регрессии у = а + bx решим систему нормальных уравнений относительно а и b :

По исходным данным рассчитываем Sх , Sу, Sух , Sх² , Sу².

Таблица 6.1

t	y	x	yx	x2	y2
1	1,70	6,07	10,3	36,86	2,9
2	4,80	10,00	48,0	100,00	23,0
3	3,70	8,81	32,6	77,61	13,7
4	6,10	12,08	73,7	145,91	37,2
5	9,40	13,24	124,5	175,28	88,4
6	9,60	9,41	90,4	88,58	92,2
7	2,10	4,29	9,0	18,37	4,4
8	2,60	5,20	13,5	27,04	6,8
9	4,50	7,26	32,7	52,68	20,3
10	8,40	8,48	71,3	71,99	70,6
11	9,70	10,43	101,2	108,79	94,1
12	2,30	5,35	12,3	28,61	5,3
13	3,40	6,07	20,6	36,86	11,6
14	6,30	10,33	65,1	106,66	39,7
15	9,80	10,83	106,1	117,26	96,0
16	7,30	9,86	72,0	97,32	53,3
17	1,80	4,62	8,3	21,30	3,2
18	2,60	6,05	15,7	36,56	6,8
19	4,80	9,41	45,2	88,58	23,0
20	16,10	12,88	207,4	165,89	259,2
21	1,30	3,82	5,0	14,62	1,7
22	2,30	5,90	13,6	34,78	5,3
23	1,30	5,20	6,8	27,04	1,7
24	3,40	6,94	23,6	48,15	11,6
25	5,60	12,87	72,1	165,73	31,4
26	2,20	8,46	18,6	71,60	4,8
27	1,90	8,44	16,0	71,31	3,6
28	6,10	8,65	52,8	74,87	37,2
29	8,20	13,23	108,5	174,92	67,2
30	3,60	11,61	41,8	134,86	13,0
31	4,60	11,22	51,6	125,88	21,2
32	2,50	10,64	26,6	113,17	6,3
33	3,40	8,61	29,3	74,09	11,6
34	6,40	16,20	103,7	262,52	41,0
35	2,30	6,57	15,1	43,18	5,3
36	1,80	9,00	16,2	81,00	3,2
Итого	173,9	318,0353303	1760,9	3119,87	1217,5
Среднее	4,83	8,83	48,9	86,7	33,8
Обозначение среднего

Найдем дисперсию переменных

= 86,7 – 4,83² = 8,62

= 33,8 – 8,83² = 10,48

Найдем параметры a и b уравнения линейной регрессии :

0,724

8,83 – 0,724 · 4,83 = – 1,57

Уравнение регрессии :

= – 1,57 + 0,724 · х

С увеличением среднего объема производства на 1 млн. руб. производительность труда увеличивается на 0,724 тыс. руб. / чел.

Нанесем линию регрессии на график корреляционного поля.

Рассчитаем линейный коэффициент парной корреляции:

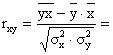
 0,656

Т.к. коэффициент от 0,3 до 0,7 связь средняя, прямая.

Практическая работа №7

 

Имеются данные об изменении себестоимости продукции в процессе освоения нового производства (табл. 7.1).

Таблица 7.1

Квартал	1	2	3	4	5	6	7	8	9	10
Себестоимость единицы, руб.	290	250	310	230	240	210	220	200	210	210

Рассчитайте для данного ряда динамики:

а) величины абсолютных изменений уровней ряда;

б) темпы изменения (%).

Постройте график и выберете формулу для аналитического выравнивания.

Рассчитайте ее параметры и нанесите теоретическую линию регрессии на график.

Решение:

Рассчитаем показатели динамики по следующим формулам:

Абсолютный прирост базисный:

D_iбаз = Y_i – Y₁ ,

где Y₁ – размер показателя в первом году, Y_i – размер показателя в i-ом году. Абсолютный прирост цепной:

D_{i цеп} = Y_i – Y_i-1 ,

где Y_i–1 – размер показателя в предшествующий i-му год.

Темп роста базисный:

Т_{р баз} = (Y_i / Y₁)·100 .

Темп роста цепной:

Т_{р цеп} = (Y_i / Y_i–1)·100 .

Темп прироста базисный:

Т_{пр баз} = Т_{р баз} – 100 .

Темп прироста цепной:

Т_{пр цеп} = Т_{р цеп} – 100 .

Рассчитанные показатели сведем в таблицу

Таблица 7.2 Показатели динамики себестоимости продукции

Квартал	Себестоимость единицы, руб.	Абсолютный прирост		Темп роста, %		Темп прироста, %
		базисный	цепной	базисный	цепной	базисный	цепной
1	290,0	–	–	100,0	–	0,0	–
2	250,0	– 40,00	– 40,00	86,2	86,2	– 13,8	– 13,8
3	310,0	20,00	60,00	106,9	124,0	6,9	24,0
4	230,0	– 60,00	– 80,00	79,3	74,2	– 20,7	– 25,8
5	240,0	– 50,00	10,00	82,8	104,3	– 17,2	4,3
6	210,0	– 80,00	– 30,00	72,4	87,5	– 27,6	– 12,5
7	220,0	– 70,00	10,00	75,9	104,8	– 24,1	4,8
8	200,0	– 90,00	– 20,00	69,0	90,9	– 31,0	– 9,1
9	210,0	– 80,00	10,00	72,4	105,0	– 27,6	5,0
10	210,0	– 80,00	0,00	72,4	100,0	– 27,6	0,0

Нанесем данные на график динамики :

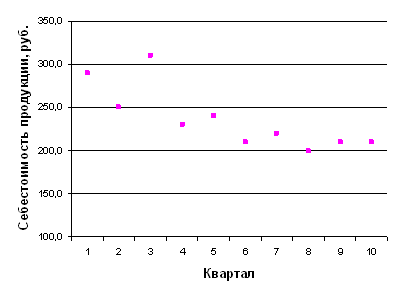
Рис. 7.1. Исходные данные.

По графику динамики можно предположить параболическую или обратную гиперболическую зависимость.

Для определения основной тенденции ряда произведем выравнивание ряда динамики с помощью уравнения параболической кривой.

Найдем оценки параметров параболической регрессии и составим уравнение линии регрессии.

Для этого необходимо решить систему из трех линейных уравнений :

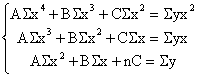
где А, В и С параметры параболической кривой :

у* = Ах² + Вх + С

Для расчетов будем использовать данные таблицы 7.3.

Таблица 7.3

i	yi	xi	x2	x3	x4	уx2	уx
1	290	1	1	1	1	290	290
2	250	2	4	8	16	1000	500
3	310	3	9	27	81	2790	930
4	230	4	16	64	256	3680	920
5	240	5	25	125	625	6000	1200
6	210	6	36	216	1296	7560	1260
7	220	7	49	343	2401	10780	1540
8	200	8	64	512	4096	12800	1600
9	210	9	81	729	6561	17010	1890
10	210	10	100	1000	10000	21000	2100
Итого	2370	55	385	3025	25333	82910	12230

Решая данную систему получим следующие значения коэффициентов

А = 0,985 ;В = – 20,591 ; С = 312,33

Т.е. уравнение параболической кривой будет выглядеть так :

у* = 0,985х² – 20,591х + 312,33

В данном случае х – это кварталы с 1 по 10.

Построим график изменения показателя и полученной тенденции.

Рис. 7.2. Исходный и выровненный ряды

По графику видно, что полученная параболическая функция достаточно точно совпадает с исходными данными.

Практическая работа №8

 

Данные о реализации товаров в магазине за два квартала приведены в табл. 8.1.

Таблица 8.1

Товары	Товарооборот в фактических ценах, млн. руб.		Изменения цен в % к базисному периоду
	базисный период	отчетный период
А	141,5	262,6	+4
Б	122,5	121,0	– 2
В	136,0	148,8	без изменений

На основе приведенных данных вычислите:

а) общий индекс товарооборота в фактических ценах;

б) индивидуальные и общий индексы цен;

в) индивидуальные и общий индексы физического объема;

г) абсолютные изменения товарооборота в целом и по факторам (влияние цен и влияние физического объема продаж) как по отдельным товарам, так и в целом.

Результаты расчетов сведите в таблицу и сделайте выводы.

Решение:

Рассчитаем недостающие и суммарные значения поставок базисного периода, отчетного периода и отчетного в ценах базисного для всех товаров.

Индивидуальные индексы цен найдем через приросты:

i_p = (100 + Δp%) / 100%

i_{p А} = (100 + 4) / 100 = 1,04

i_{p Б} = (100 – 2) / 100 = 0,98

i_{p В} = (100 + 0) / 100 = 1,0

Показатели сведем в таблицу:

Таблица 8.2 Расчет суммарных товарооборотов

Товарные группы	Товарооборот, млн. руб.		Индивидуальный индекс цен, ip	Товарооборот в отчетном периоде по ценам базисного периода, p0q1 =- p1q1 / ip
	Базисный период, p0q0	Отчетный период, p1q1
А	141,5	262,6	1,065	246,6
Б	122,5	121,0	0,98	123,5
В	136,0	148,8	1,0	148,8
Итого	400	532,4		518,9

Общий индекс объема товарооборота в фактических ценах найдем по формуле :

I_R = 523,4 / 400 = 1,3085 или 130,85 %

где R₁ , R₀ – товарооборот отчетного и базисного периодов соответственно; R_0,1– товарооборот отчетного периода в ценах базисного; p₁ , р₀ – цены отчетного и базового периода соответственно; q₁ , q₀ – объем товаров отчетного и базового периода соответственно.

Общий индекс цен по формуле :

I_p = 523,4 / 518,9 = 1,0087

Т.е. цены в среднем возросли на 0,87 %.

Найдем общую сумму перерасход (+) или экономии (–) средств в результате изменения цен.

Э = R₁ – R_0,1

Э = 523,4 – 518,9 = 4,5 млн. руб.

В результате роста цен население при покупке товаров перерасходовало 4,5 млн.руб.

Индивидуальные индексы товарооборота найдем по формуле:

i_q = q₁ / q₀ = p₀q₁ / p₀q₀

i_{q A} = 246,6 / 141,5 = 1,743

i_{q Б} = 123,5 / 122,5 = 1,008

i_{q В} = 148,8 / 136,0 = 1,094

Общий индекс объема товарооборота в сопоставимых ценах (физического объема товарооборота) найдем по формуле:

I_R,q = 518,9 / 400,0 = 1,2973 или 129,73%

Найдем абсолютное изменение объема товарооборота:

ΔR = R₁ – R₀

ΔR = 532,4 – 400,0 = 132,4 млн. руб.

Найдем изменение объема товарооборота за счет изменения физического объема продаж товаров:

ΔR_(q) = Sp₀q₁ – Sp₀q₀ = R_0,1 – R₀

ΔR_(q) = 518,9 – 400,0 = 118,9 млн. руб.

Т.е. за счет роста физического объема продаж товарооборот возрос на 118,9 млн. руб.

Найдем изменение объема товарооборота за счет изменения цен:

ΔR_(p) = Sp₁q₁ – Sp₀q₁ = R₁ – R_0,1

ΔR_(p) = 532,4 – 518,9 = 13,5 млн. руб.

Т.е. за счет роста цен товарооборот возрос на 13,5 млн. руб.

Сведем результаты в таблицу:

Таблица 8.3

Товарные группы	Товарооборот, млн. руб.		Индекс цен	Индекс физического объема
	Базисный период, p0q0	Отчетный период, p1q1
А	141,5	262,6	1,065	1,743
Б	122,5	121,0	0,98	1,008
В	136,0	148,8	1,0	1,094
Итого	400	532,4	1,0087	1,2973