Показатели расслоения

2. Показатели расслоения

Условие разложимости - это определение разложимого функционала J: функционал J называется разложимым, когда он, после подходящего монотонного преобразования, может быть представлена в виде уже приведенной суммы, где F₀ - смесь функций распределения F_i в группах. В этом определении сразу дано такое представление функции J, которое могло бы быть дано в два этапа, первый - определение разложимости как некоторой зависимости от функций распределения в группах и на их центрах, и второй - приведение к аддитивной зависимости после монотонного преобразования. Если далее определить показатель (или меру) расслоения (или неравенства) I как разложимый функционал J, удовлетворяющую условиям 1-7, то может быть доказана следующая теорема.

Теорема. Непрерывно дважды дифференцируемая разложимая мера расслоения удовлетворяет условиям передачи и однородности тогда и только тогда, кода она имеет вид

 

для некоторого a³0, где m(F) - центр распределения F, а w_a(x) - решение уравнения x(d²w(x)/dx²)+(1-a)(dw/dx)=b.

Если учесть, что решения w(x) дифференциального уравнения xw”+(1-a)w’=b и соответствующие им p(F_l) имеют вид

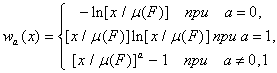 и p_a(F_l)=[l/m(F)]^a,

то общим видом показателя расслоения будет следующий

.

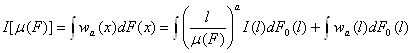Смешивающая функция для дискретных величин F₀(l) в точке l=m(F_i) имеет скачёк величины l_i, для непрерывного случая аналогично.

Результат теоремы состоит, во-первых, в том, что мера расслоения не зависит от численности общества (или групп), а зависит лишь от функции распределения. Во-вторых, характеристических (существенных) свойств всего два - однородности и передачи.

Все остальные следуют из них. Таким образом, не было необходимости приводить и описывать все свойства расслоения, хотя они многое проясняют. Более того теорема показывает, что меру расслоения можно искать в виде  и функция w(x) связана с множеством решений уравнения xw”(x)+(1-a)w’(x)=b.

 

3. Частные показатели

 

Осталось привести лишь частные случаи. При a=0 имеем

 

I(F)=,

при a=1 получается мера расслоения Тайла (Theil):

 

I(F)=,

наконец, при a=2 имеем квадрат коэффициента вариации:

 

I(F)=,

множители перед интегралом опущены в соответствии с определением разложимости.

Рассмотрим общество, заданное функцией распределения F, состоящее из m групп, каждая из которых определяется своей функцией распределения F_i (). В этом случае F=, где l_i³0, и Sl_i=1. Кроме того, чтобы F была функцией распределения всего общества необходимо представление распределения центров групп в виде F₀(x)=S_iH(x-x_i)l_i, где H(x) - функция Хевисайда, т.е. она равна 1 при x³0 и 0 в других случаях, а l_i=n_i/n и x_i=m(F_i).

Остается привести лишь разложения уже приведенных показателей расслоения.

Для первого показателя - логарифмической меры расслоения - имеем функцию w(x)=-ln[x/m(F)], которая дает название меры. Для нее весовая функция p имеет вид p[m(F_i)]=1. а показатель расслоения

 

I[m(F)]=,

или, в более общем виде для распределения F(x)=, где F(x/l)=F_i(x) при l=m(F_i),

.

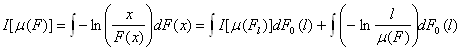Для меры неравенства Тейла функция w(x)=[x/m(F)]ln[x/m(F)], весовая функция p[m(F_l)]=[l/m(F)], поэтому,

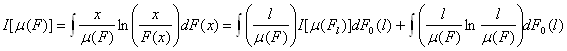
Для квадрата коэффициента вариации функция w(x)=[x/m(F)]²-1, весовая функция p[m(F_l)]=[l/m(F)]² и

.

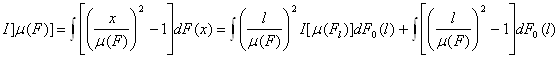В самом общем виде для функции w(x)=[x/m(F)]^a-1 весовая функция p[m(F_l)] будет равна [l/m(F)]^a, а разложимый показатель расслоения для любого a имеет вид

.

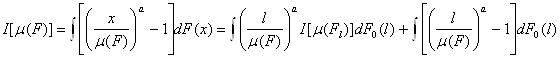Для того, чтобы убедиться в неотрицательности любого из приведенных показателей бедности следует проделать следующее. Во-первых, все представленные в показателях расслоения весовые функции w(x) выпуклы. Во-вторых, все функции распределения F_l таковы, что их средние значения равны единице. В-третьих, для выпуклых функций w справедливо неравенство Йенсена Ew(X)³w(EX). Теперь, применив неравенство Йенсена к весовой функции w[x/m(F)] получаем требуемый результат.

Последнее обстоятельство, на которое необходимо обратить внимание, заключается в том, что функция Лоренца разложима в смысле уже данного определения. Действительно, пусть F(w)=Sl_IF_i(w). Тогда справедливо равенство L(w)=(1|W)Sl_iW_iL_i(w), которое следует из определения функции Лоренца после вынесения из-под знака интеграла Sl_i и умножения каждого слагаемого на W_i/W_i. Легко убедиться, что сумма весов (l_IW_i/W) последнего соотношения равна 1. Однако коэффициент Джини неразложим. Наконец, энтропия распределения, представляющего собой функцию Лоренца, это разложимая мера расслоения Тейла.

ЗАДАЧИ

1. Получите с помощью таблицы из приложений к гл. 3 логарифмическую меру расслоения.

2. Получите с помощью таблицы из приложений к гл. 3 меру расслоения Тейла.

3. Получите с помощью таблицы из приложений к гл. 3 меру расслоения, основанную на квадрате коэффициента вариации.

Справки и ссылки

Глава базируется в основном на известных работах о разложимых показателях Fracois Bourguignon’а и Antony F.Shorrocks’а. В этих работах, по-видимому, впервые был поставлен вопрос о показателях со свойством разложимости. Само это свойство было подмечено ранее, как явствует из названия показателя Тейла, ссылка на которую имеется в уже упомянутых работах. Однако сами работы замечательны не только постановкой задачи, но и её решением. Более того, именно в них сформулированы предположения, изложенные в это главе. Вывод самих показателей имеется в упомянутой работе Шорокса.

Литература

 

1.     Бартоломью Д. Стохастические модели социальных процессов. Изд. “Финансы и статистика”, Москва, 1985 г.

2.     Бедность: альтернативные подходы к определению и измерению. Cornegie Endowment for International Peace. М. 1998 г.

3.     Белкина Т.А., Лёвочкина М.С. Исследование модели оптимального управления негосударственным пенсионным фондом. В сборнике «Математические модели экономики». Изд. МГИЭМ, 2002

4.     Борокин Ф.М., С.В. Соболева. Прогнозирование миграции и численности населения системой дифференциальных уравнений. Сборник Математические методы в социологии. Новосибирск, 1974 т.

5.     Бреев Б.Д. Староверов О.В. Об одном методе учёта факторов в движении населения. «Экономика и математические методы», №1, 1979 г.

6.     Гаврилец Ю.Н. Компромисс интересов и справедливость в оплате труда (модельный анализ). «Экономика и математические методы», том 28, выпуск 1. 1992 г.

7.     Гаврилец Ю.Н. Модель равновесного функционирования экономики с переменной структурой населения. «Экономика и математические методы», том 30, вып. 2, 1994 г.

8.     Гегель Г. Политические произведения, Изд. "Наука". М. 1978г