Навигация
Распределения и меры расслоения доходов
18516
знаков
3
таблицы
0
изображений
Реферат
на тему:
"Распределения и меры расслоения доходов"
Москва, 2008
Введение
Душевой доход, как уже стало ясно, варьирует довольно значительно, поэтому во всех странах стараются иметь сравнительно малые доходные группы (слои) с доходами, скажем, от 200 до 300, от 300 до 400 и т.д. и основную роль начинает играть доля людей, принадлежащих к каждой из них. Поэтому изучение вопросов распределения членов общества по доходам (или доходов по людям) имеет богатую историю и много граней. Но далее будет рассматриваться лишь один аспект этой большой проблемы: каково расслоение общества и какова мера этого расслоения. Часто вместо термина «расслоение» употребляют аналогичные, например, «дифференциация», «рассеяние» и даже «неопределенность» доходов или термины противоположного смысла, скажем, «концентрация», «сосредоточение», «определенность» и т.п.
1. Меры расслоения
Из ранее сказанного ясно, что мера расслоения должны быть тесно связаны с долей людей, имеющих доход меньший x рублей. Эта доля изучается теорией вероятностей и обычно там обозначается F(x). Кроме того, мера расслоения должна удовлетворять некоторым требованиям:
1. Мера расслоения минимальна, когда доходы всех людей одинаковы (расслоения нет);
2. Мера расслоения увеличивается при увеличении разброса доходов;
3. Мера расслоения не зависит от единицы измерения доходов.
Требование 1 выполняется тогда, когда при одинаковых доходах значение меры минимально (удобнее, когда оно равна 0). Тогда мера расслоения положительна и тем больше, чем больше отличаются доходы разных людей друг от друга.
Наиболее полно меры расслоения изучаются теорией вероятностей, где обычно говорят не просто о мерах расслоения, а о рассеянии. Мерой рассеяния в теории вероятностей служит энтропия E распределения F(x), которая задаётся так:
E=-MlnF’ (x)
где x – случайная величина, распределенная по закону F(x). Для случайных величин, душевых доходов отдельного человека, на которого в домохозяйстве приходится x1, x2,…, или xn денежных единиц, с вероятностями p1, p2,…, pn (
), энтропия E вычисляется с помощью следующего соотношения:
Для непрерывных случайных величин, имеющих плотность f(x)=F’ (x), энтропия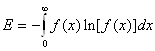 
.
Очевидно, что для дискретных случайных величин энтропия E удовлетворяет неравенству 0£E£Em, где Em – максимальное значение энтропии. Распределение, соответствующее Em, можно найти, как впрочем, можно найти и распределения, соответствующие другим мерам расслоения.
2. Примеры
Пример 1. Рассмотрим доходы xi =a+(i‑1) h, где a – минимальный доход, а h – шаг дискретности, скажем, равный денежной единице. Если среднедушевые доходы ограничены величиной b, то всего градаций доходов будет n, где n=m+1, а m=(b-a)/h, т.е. x1=a, x2=a+h, x3=a+2h,…, xn =b. Если верхнюю границу указать трудно, то будем считать, что последовательность x1, x2,…, xn,… не ограничена. Пусть каждому xi соответствует вероятность pi (доля людей, имеющих среднедушевой доход, равный xi).
а) Доходы ограничены и нужно найти такие pi, чтобы 
достигала максимума. Очевидно, что . Таким образом, получена задача на условный экстремум. После дифференцирования функции Лагранжа 
по pi имеем систему уравнений – lnpi -1-l 
. Откуда получаем, что pi =e-1-l, т.е. одинаковы для любого i. Из уравнения 
получаем выражение lnn‑1-l=0 для величины l и l=lnn‑1, следовательно, pi =e-1-lnn+1=e-lnn=1/n. Теперь легко получить, что в этом случае, когда все величины доходов равновероятны, Em =lnn.
б) Банковские проценты, под которые можно вложить свой капитал, если они вполне разумны, не поддаются обоснованному ограничению сверху. Но в этой ситуации, как правило, заданы минимальные проценты – r, а также среднее значение всех процентов – b. Теперь появляется задача: найти такие pi, которые давали бы максимум 
при ограничениях 
и 
, где первые m значений pi=0, а значения xi=ih, когда i=m, m+1,…. С учетом всех ограничений функция Лагранжа будет равна
.
Принимая во внимание, что первые p1, p2,… pm – равны 0, так как минимум процента r=hm=xm, то можно найти (см. задачу 1)
,
где 
. В этом случае
=lnx/(1‑x).
в) Рассмотрим задачу из пункта а) этого примера, но в качестве меры расслоения возьмем не энтропию, а дисперсию. Попытка решить задачу так же, как в пункте а) приводит к выводу, что экстремума внутри области (симплекса 
и 
) нет. Следовательно, задачу нужно решить на границе симплекса. Для простоты, рассмотрим какие-либо точки душевых доходов, x (не обязательно =a) c, и y (не обязательно =b) и соответствующие им доли людей (вероятности) обозначим p и q, оставшиеся на остальные точки xi вероятности обозначим через 
(g=p+q), т.е. 1-g=
. По сути дела задача свелась к следующей: пусть заданы три величины среднедушевого дохода x£c£y, которые случайно выбранный из популяции человек имеет с вероятностями p, (1-g) и q. В этом случае, дисперсия равна D=x2p+y2q+c2(1-g) – [xp+yq+c (1-g)]2. Можно показать (см. задачу 2), что
D=p (1‑p) (y-x)2 – (1-g) [2y (y-x)+g(y2-c2)+2c (xp+yq)].
Поэтому последнее слагаемое неотрицательно и оно равно 0 при p+q=1, т.е. при 1-g=0. Отсюда следует, что maxD=p (1‑p) (b-a)2 при заданном p, maxD=p (1‑p) (y-x)2 при заданных x и y и 
при всех (x, y, p) свободных параметрах.
Рассматривать аналог пункта б) для дисперсий не имеет смысла, так любое распределение, имеющее математическое ожидание при несуществующей дисперсии дает ответ.
Замечание 1 к примеру 1б. Все выведенные распределения имеют непрерывные аналоги; так для пункта а) таким аналогом будет равномерное распределение на отрезке [a, b]. Для пункта б) аналогом будет показательное распределение с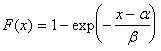 
и плотностью 
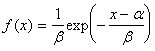, отличными от 0 при x³a.
Замечание 2 к примеру 1б. Представляет интерес получить распределение с наибольшей энтропией не только при заданном среднем значении, но и заданной дисперсии. Для дискретного случая задача не решена, а для непрерывной случайной величины с неограниченным в обе стороны диапазоном ответ известен: распределение будет нормальным.
Пример 1 показывает, что всякое расслоение в том числе и в обществе из-за различных среднедушевых доходов можно мерить и дисперсией и энтропией, так как и та и другая мера равна 0 при равенстве среднедушевых доходов и растет при расслоении. Однако необходимо привести недостатки приведенных мер.
Похожие работы
... , Для квадрата коэффициента вариации функция w(x)=[x/m(F)]2-1, весовая функция p[m(Fl)]=[l/m(F)]2 и . В самом общем виде для функции w(x)=[x/m(F)]a-1 весовая функция p[m(Fl)] будет равна [l/m(F)]a, а разложимый показатель расслоения для любого a имеет вид . Для того, чтобы убедиться в неотрицательности любого из приведенных показателей бедности следует проделать следующее. Во- ...
... роста. Однако их прирост в каждом следующем году относительно предыдущего замедляется: в 2005 г. он составил 11,1%, в 2006 г. – 11,0%, в 2007 г. – 10,4%. Сократилась межрегиональная дифференциация доходов – например, среднедушевые доходы населения в г. Москве, были в 2007 г. в 6,1 раза выше соответствующего показателя, рассчитанного для Ивановской области (минимальный размер душевых доходов среди ...
... домашними хозяйствами для собственного конечного потребления; - потребление продуктов, полученных домашними хозяйствами в натуральной форме в качестве оплаты труда; - услуги по проживанию в собственном жилище. Статистические методы изучения доходов, потребления и социальной защиты Основными источниками данных о доходах и расходах населения являются данные государственной и ...
... начнут проводить общую политику, то их совместная рыночная власть и вовсе приблизится к той, которой обладает монополия. 3. Дифференциация заработной платы при социализме Дифференциация заработной платы – установление неодинаковых уровней заработной платы для различных категорий работников в отдельных отраслях народного хозяйства и районах страны. Отражает различие в продолжительности и ...
0 комментариев