Пример решения задачи по механике

Рассчитать закрытую не реверсивную цилиндрическую косозубую передачу по ниже следующим данным:

N=95000 Вт=95 кВт; ;  

Принимаем предварительный коэффициент К=1,4 (зубчатые колёса расположенны у середины пролёта, но нагрузки на разных концах валов могут дополнительно изгибать валы).

Зная мощность цилиндрической косозубой передачи, мы можем найти момент на зубчатом колесе.

где

Теперь определяем передаточное число передатки:

По ГОСТу 8032-56 принимаем передаточное число i=7,1

Так как материалы для шестерни и для зубчатого колеса не заданы нам, то ма выбираем их в справочнике. Так для шестерни принимаем улучшенную сталь 40ХА с НВ285, которая имеет контактную прочность зуба  и

Для зубчатого колеса принимаем улучшенную сталь 50, с твёрдостью НВ280 и допускаемые напряжения  

В справочнике по графику ;   (для материала зубчатого колеса), и К=1,4 для косозубых колёс межосевое расстояние

Зная межосевое расстояние принимаю число зубьев шестерни , далее находим число зубьев зубчатого колеса. .

Принимая число зубьев зубчатого колеса равное 170

После этого назначаю предварительно угол наклона зубьев , тогда. Далее беру значения  и определяем нормальный модуль передач по формуле:

В соответствии ГОСТом 9563-60, принимаю нормальный модуль равный

Зная нормальный модуль, межосевого расстояния и числу зубьев шестерни

Угол наклона зубьев.

Тогда по таблице Брадиса находим, что

Однако, мы можем сделать другую последовательность расчёта.

По этому принимаю нормальный модуль по соотношению

По ГОСТу 9563-60 можно принять нормальный модуль

Чтобы определить суммарное число зубьев назначу предварительно угол наклона зубьев . Тогда . Остановимся предварительно на значении равном , тогда суммарное число зубьев . Отсюда следует, что число зубьев шестерни равно:

Следовательно принимаю число зубьев шестерни

Теперь определяю число зубьев колеса

Принимаю число зубьев колеса

Окончательное суммарное число зубьев

Тогда значение ; Угол наклона зубьев

После основных подсчётов, мы определяем размеры шестерни колеса, т.к. нам известнымодуль и

Зная размеры шестерни колеса проверяем соблюдение условия:

 т.е. в нашем случае

Теперь получаем другие размеры колеса и шестерни необходимые для изготовления.

Зная коэффициент ширины колеса равные  и межосевое расстояние, находим ширину колеса:

, а ширина шестерни в свою очередь:

Нам уже известно  и , поэтому мы можем определить окружную скорость:

В справочнике по таблице при данной скорости для косозубых зубьев цилиндрической передачи мы можем принять  степень точности, но для уменьшения динамической нагрузки выбираем  степень точности.

Так как мы предварительно принимали коэффициент ширины колеса, то теперь мы его уточняем по таблице в справочнике в зависимости от того, что

U  степени точности, для колёс находим . Мы знаем  и по этому определяем  по формуле

В справочнике по таблице для скорости 6,1 м/с при твёрдости до НВ350 для восьмой степени точности находим

Нам уже известно, что  и , по этому находим окончательный коэффициент нагрузки по формуле:

Так как нам известны все значения для проверки расчётного контактного напряжения, то это именно мы и выполним по формуле:

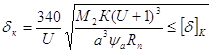
После подстановки получаем

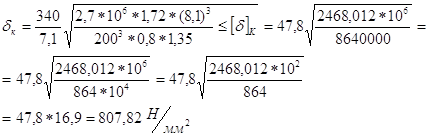
Далее смотрим есть ли у нас перенапряжение:

 что допустимо

Проверка прочности зубьев на изгиб

Для шестерни

Для колеса

Зная, что мы нашли  и  исходя из этого находим коэффициенты формы зуба в справочнике.

Для  коэффициент будет равен 0,404.

Для  коэффициент будет равен 0,4881.

Так как мы нашли коэффициенты формы зуба, то теперь можем сделать сравнительную оценку прочности на изгиб зубьев шестерни и колеса.

Так же следует проверить на изгиб зубья колёса, т.к. их прочность ниже, чем прочность шестерни;

Теперь находим расчётное напряжение изгиба в опасном сечении зуба колеса по формуле:

 - коэффициент учитывающий повышенную нагрузочную способность косозубых передач по сравнению с прямозубыми передачами за счёт увеличения контактных линий. Для прямозубых колёс , а для косозубых и конических от 1,15 до 1,35

Список литературы

Для подготовки данной работы были использованы материалы с сайта http://goldref.ru/