М(Koy) Koy

35000 М(Koy) Koy

Согласно [1] составим систему уравнений:

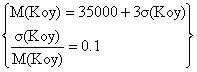
  Koy=50000±30%

Аналогично определяем Rbx .Получаем Rbx=430 кОм±30%.

Т.о. получили Koy=50000±30% Rbx=430 кОм±30%

10) На основе данных, приведённых в [2] получили стабильность Koy и Rbx :

а)Температурная : a Koy= ±25×10^-2 %  при Т = -60°…+100° С;

a Rbx = ±7,5×10^-3 %  при Т = -60°…+100° С;

б)Временная: С Koy= ±3×10^-3%; С Rbx= ±5×10^-4 % ;

11) Коэффициент корреляции между Koy и Rbx: r =0.8

1.2 Пояснение решаемой задачи

В курсовом проекте необходимо произвести оценку параметрической надёжности РЭС, с использованием моделирования на ЭВМ постепенных отказов элементов.

Оценка параметрической надёжности - определение основных количественных показателей сохранения рабочих функций при возможных постепенных изменениях параметров комплектующих элементов в условиях эксплуатации.

Оценку параметрической надежности будем проводить следующим способом: Подсчитав по формуле (1.1) выходной параметр K (коэффициент передачи) и установив допуск на выходной параметр DK, смоделируем n РЭУ. РЭУ будем считать работоспособным, если значение коэффициента передачи лежит в диапазоне установленного допуска, т.е. K±DK. Таким образом, найдём вероятность отсутствия параметрического отказа (см. раздел 2).

2. ВЫБОР МЕТОДА РЕШЕНИЯ ПОСТАВЛЕННОЙ ЗАДАЧИ

Метод решения задачи состоит в следующем. Определяем выходной параметр по формуле (1.1) по значениям параметров элементов, не учитывая производственные допуска, корреляцию, воздействия температуры и времени. Назовем полученный таким образом коэффициент передачи “идеальным” -- K_и. После чего задаемся допуском на выходной параметр DK_и, в пределах которого РЭУ считается исправным.

При помощи ЭВМ моделируем n различных реализаций РЭУ с параметрами элементов, распределенных либо по нормальному закону, либо по равномерному закону. Затем пересчитываем значения параметров элементов при воздействии на них температуры и времени. При этом предполагаем, что температурный коэффициенты a_R, а также коэффициенты старения С_R распределены по нормальному закону, а температура окружающей среды Т_раб – по равномерному. В связи с тем, что закон распределения температуры окружающей среды был неизвестен, и не было возможности попытаться подобрать закон распределения экспериментально, то была принята гипотеза о том, что температура распределена по равномерному закону, так как эта модель на практике является предельным (наихудшим) случаем разброса параметра. Определяем выходной параметр по формуле (1.1) – этот коэффициент передачи назовем “реальным”(K_р).

По способу, изложенному в подразделе 1.2, вероятность отсутствия параметрического отказа определим следующим образом:

Р (K_н £ K_р £K_вt_зад)= , (2.1)

где n_исп – число исправных РЭУ на момент времени t_зад;

N – общее число смоделированных РЭУ;

K_н – нижнее значение коэффициента передачи K_н = K_и - DK_и;

K_в – верхнее значение коэффициента передачи K_в = K_и + DK_и.

Определяем математическое ожидание выходного параметра М*(K_р) и его среднеквадратичное отклонение s*(K_р) по формулам [1]:

М*(K_р) = , (2.2)

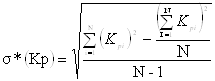 (2.3)

3. РЕШЕНИЕ ЗАДАЧИ НА ЭВМ

 

3.1 Описание вычислительного алгоритма моделирования температурных и временных изменений параметров

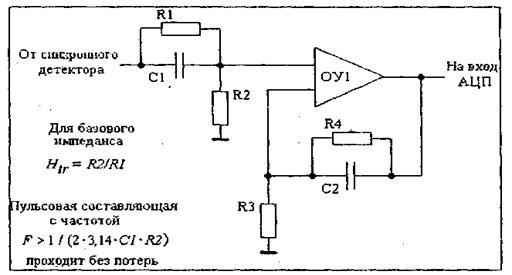
R1, R2, R3 - сопротивления 1-го, 2-го и 3-го резисторов;

Rbx - входное сопротивление, Koy - коэффициент усиления.

1. При помощи стандартной функции Random генерируем равномерно распределённое значение температуры: temp.

Здесь вычислительный алгоритм разделяется на 2 части:

а) Если температура попала в положительную область диапазона рабочих температур т.е  20,

то, используя формулу (3.1) [1] генерируем нормально распределённые значения температурных коэффициентов a_R+, a Rbx : dx1,dx2,dx3,dx 4.

a_R+ - температурный коэффициент для резисторов в полож-й области температур;

a Rbx - температурный коэффициент для входного сопротивления.

dx1, dx2, dx3, dx4 – сгенерированные значения температурных коэффициентов для

1-го, 2-го, 3-го резисторов и входного сопротивления соответственно.

б)Если температура попала в отрицательную область диапазона рабочих температур т.е  20,

то, используя формулу (3.1) [1] генерируем нормально распределённые значения температурных коэффициентов a_R+ , a Rbx : dx1,dx2,dx3,dx4.

a_R- - температурный коэффициент для резисторов в отриц-й области температур;

a Rbx - температурный коэффициент для входного сопротивления.

dx1, dx2, dx3, dx4 – сгенерированные значения температурных коэффициентов для

1-го, 2-го, 3-го резисторов и входного сопротивления соответственно.

x = s×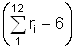+ m, (3.1)

где x – нормально распределённое случайное число;

m – математическое ожидание;

s – среднеквадратичное отклонение;

r_i – стандартное равномерно распределенное случайное число в диапазоне 0..1. (r_i получаем при помощи стандартной функции Random).

Далее пересчитываем значения первичных параметров (R1,R2, R3, Rbx) с учётом воздействия температуры. Для этого воспользуемся формулами [1]:

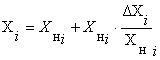 (3.2)

где – номинальные значения i-го первичного параметра;

–приращения значений i-го первичного параметра под действием температуры;

Согласно [1] относительное изменение i-го первичного параметра под воздействием температуры (старения) можно выразить следующим образом:

 (3.3)

(3.4)

где – температурный коэффициент i-го первичного параметра;

°C,

где t_ср – температура окружающей среды;

с_i – коэффициент старения i-го первичного параметра;

– рассматриваемый интервал времени.

В качестве t_ср для положительной области диапазона рабочих температур примем

наибольшую из возможных температур - Tv, а для отрицательной области примем наименьшую из возможных температур - Tn. С учётом этого и формул (3.3) и (3.4) формула (3.2) примет вид:

для ‘‘+‘‘ -ой области температур:

 (3.5)

С учётом этой формулы получаем:

;; ;;

для ‘‘-‘‘ -ой области температур:

 (3.6)

С учётом этой формулы получаем:

;;

;;

где Rtemp1, Rtemp2, Rtemp3 - значения сопротивлений 1-го, 2-го и 3-го резисторов соответственно с учётом действия температуры.

RWtemp – значение входного сопротивления под действием температуры.

SR1, SR2, SR3 – номинальные значения 1-го, 2-го и 3-го резисторов соответственно.

SRW – номинальное значение входного сопротивления.

Для получения значений коэффициента усиления (Koy) производим смещение параметров m = m(z) и s = s(z) его температурного коэффициента (a Koy) с учётом коэффициента парной корреляции , а затем, воспользовавшись подпрограммой формирования случайных нормально распределённых чисел с параметрами m = m(z/x) и s = s(z/x) генерируем нормально распределённое значение его температурного коэффициента(a Koy):dx5.

dx5 - сгенерированное значение температурного коэффициента для коэффициента усиления.

Воспользовавшись формулой (3.5) (для положительной области температур) или (3.6) (для отрицательной области температур) пересчитываем значения коэффициента усиления (Koy) с учётом воздействия температуры:

для ‘‘+‘‘ -ой области температур:

;

для ‘‘-‘‘ -ой области температур: ;

где KOUtemp – значение коэффициента усиления под действием температуры.

SKOU – номинальное значение коэффициента усиления.

В отрицательной и положительной области температур по формуле (1.1) определяем значение выходного параметра - коэффициента передачи (Kexit).

2. Используя формулу (3.1) генерируем нормально распределённые значения коэффициентов старения С_R, С Rbx :dx1,dx2,dx3,dx4.

С_R – коэффициент старения для резисторов;

С Rbx – коэффициент старения для входного сопротивления;

dx1, dx2, dx3, dx4 – сгенерированные значения коэффициентов старения для

1-го, 2-го, 3-го резисторов и входного сопротивления соответственно.

Воспользовавшись формулой:

 (3.7)

пересчитываем значения первичных параметров (R1,R2, R3, Rbx) с учётом воздействия старения:

;;

;;

где Rtime1, Rtime2, Rtime3 - значения сопротивлений 1-го, 2-го и 3-го резисторов соответственно с учётом действия старения.

RWtime – значение входного сопротивления под действием старения.

SR1, SR2, SR3 – номинальные значения 1-го, 2-го и 3-го резисторов соответственно.

SRW – номинальное значение входного сопротивления.

Для получения значений коэффициента усиления (Koy) производим смещение параметров m = m(z) и s = s(z) его коэффициента старения(С Koy) с учётом коэффициента парной корреляции , а затем, воспользовавшись подпрограммой формирования случайных нормально распределённых чисел с параметрами m = m(z/x) и s = s(z/x) генерируем нормально распределённое значение его коэффициента старения(С Koy):dx5.

Воспользовавшись формулой (3.7) пересчитываем значения коэффициента усиления (Koy) с учётом воздействия старения:

;

где KOUtime – значение коэффициента усиления под действием температуры.

SKOU – номинальное значение коэффициента усиления.

По формуле (1.1) определяем значение выходного параметра: коэффициента передачи (Kexit).

3.2 Пояснение процедур и функций, используемых в программе

В написанной программе формула (3.1) реализована через функцию:

Function Generator(m:Real;s:Real):Real;

Label L1;

BEGIN

L1:x:=0;

FOR i:=1 TO 12 DO

BEGIN

k:=Random;

x:=x+k;

END;

x:=x-6;

if (x>3) or (x<-3) then goto L1;

m:=m+s*x;

Generator:=m;

END;

Таким образом, введя Generator(m,s)получим случайное число, распределенное по нормальному закону с параметрами m = m и s = s.

В соответствии с [1] формула получения случайных чисел, распределенных по равномерному закону с параметрами a и b следующая:

x = ×r+ a, (3.8)

где a, b – параметры равномерной модели;

r –стандартное равномерно распределенное случайное число в диапазоне 0..1.

В написанной программе формула (3.8) реализована через функцию:

Function Generator2(m:real;s:real):Real;

BEGIN

k:=Random;

m:=(s-m)*k+m;

Generator2:=m;

end;

Таким образом, введя Generator2(m, s)получим случайное число, распределенное по равномерному закону с параметрами a=m и b = s.

Пусть случайное число x, имеющее нормальное распределение с параметрами m = m(x) и s = s(x), уже получено. Тогда для получения случайного числа z, имеющего нормальное распределение с параметрами m = m(z) и s = s(z) и коррелированного с x, необходимо произвести смещение параметров m = m(z) и s = s(z) с учётом коэффициента парной корреляции, а затем воспользоваться подпрограммой формирования случайных нормально распределённых чисел с параметрами m = m(z/x) и s = s(z/x):

(3.9)

(3.10)

Определение величины смещения параметров m = M(z) и s = s(z) с учётом коэффициента парной корреляции в соответствии с формулами (3.9) и (3.10) в программе реализовано следующим образом:

Procedure Corr(x1,mx,mz,sx,sz:real; Var mzx,szx:real);

BEGIN

mzx:=mz+rxz*(sz/sx)*(x1-mx);

szx:=sz*sqrt(1-sqr(rxz));

END;

Таким образом, введя Corr(x1,mx,mz,sx,sz,mzx,szx) получим случайное число, распределенное по нормальному закону с параметрами m = mzx и s = szx.

3.3 Обоснование выбора числа реализаций