Методы контроля параметров полупроводниковых материалов: проводимости, концентрации, подвижности, ширины запрещенной зоны

3. Методы контроля параметров полупроводниковых материалов: проводимости, концентрации, подвижности, ширины запрещенной зоны

 

3.1 Проводимость полупроводников

При приложении электрического поля к однородному полупроводнику в последнем протекает электрический ток. При наличии двух типов свободных носителей – электронов и дырок – проводимость σ полупроводника будет определяться суммой электронной σn и дырочной σp компонент проводимости σ=σn+σp.

Величина электронной и дырочной компонент в полной проводимости определяется классическим соотношением:

 (3.1)

где  и  – подвижности электронов и дырок соответственно.

Для легированных полупроводников концентрация основных носителей всегда существенно больше, чем концентрация неосновных носителей, поэтому проводимость таких полупроводников будет определяться только компонентой проводимости основных носителей. Так, для полупроводника n-типа:

 (3.2)

Величина, обратная удельной проводимости, называется удельным сопротивлением:

 (3.3)

Здесь ρ – удельное сопротивление, обычно измеряемое в единицах [Ом·см]. Для типичных полупроводников, используемых в производстве интегральных схем, величина удельного сопротивления находится в диапазоне ρ = (1 ÷ 10) Омсм.

В отраслевых стандартах для маркировки полупроводниковых пластин обычно используют следующее сокращенное обозначение типа: КЭФ – 4,5. В этих обозначениях первые три буквы обозначают название полупроводника, тип проводимости, наименование легирующей примеси. Цифры после букв означают удельное сопротивление, выраженное во внесистемных единицах, – Ом·см. Например, ГДА – 0,2 – германий, дырочного типа проводимости, легированный алюминием, с удельным сопротивлением ρ = 0,2 Ом·см; КЭФ – 4,5 – кремний, электронного типа проводимости, легированный фосфором, с удельным сопротивлением ρ = 4,5 Ом·см.

3.1.1 Преимущества и недостатки методов исследования проводимости полупроводников

При определении электропроводности методом термозонда в отличие от метода Холла нельзя вычислить подвижности дырок и электронов, т.е. методом термозонда невозможно определить какие-нибудь точные значения. Но метод термозонда уступает методу Холла в простоте определения типа электропроводности, нет сложных просчетов и сам опыт не предоставляет собой довольно сложные лабораторные исследования. Недостатком метода вольтамперной характеристики является то, что при определении проводимости этим методом желательно, чтобы поверхность образца полупроводника была шероховатой (шлифованной), а не полированной, т. к. при шлифованной поверхности осциллограмма более четко выражена и по ней легче определить тип проводимости образца.

 

3.2 Определение подвижности

Под действием внешнего электрического поля носители заряда приобретают некоторую скорость направленного движения (скорость дрейфа) и создают электрический ток. Отношение средней установившейся скорости направленного движения к напряженности электрического поля называют подвижностью носителей заряда:

μ = . (3.4)

В полупроводниках следует различать подвижность электронов μ_п и подвижность дырок μ_р. С учетом двух типов носителей заряда выражение плотности тока принимает вид:

 

J = en₀μ_пE+ ep₀μ_pE, (3.5)

где п₀ и р₀ – равновесные концентрации электронов и дырок в полупроводнике.

С помощью закона Ома из (1) легко получить формулу для удельной проводимости полупроводника:

γ = en₀μ_п + ep₀μ_p. (3.6)

В примесных полупроводниках, как правило, одним слагаемым из выражения (2) можно пренебречь. Например, при достаточно большой концентрации доноров в полупроводнике вклад дырок в электропроводность ничтожно мал. В большинстве случаев подвижность дырок меньше подвижности электронов.

3.2.1 Факторы, определяющие подвижность

Согласно экспериментальным данным у некоторых полупроводников подвижность носителей заряда может быть на несколько порядков больше, чем у металлов, то есть электроны в плохо проводящих кристаллах могут двигаться более свободно, чем в металлах.

Дрейфовая скорость, а значит и подвижность носителей заряда, тесно связаны с их длиной свободного пробега в кристалле:

μ =·τ₀ = ·, (3.7)

где m* – эффективная масса носителей заряда;  – тепловая скорость.

Большая подвижность может быть обусловлена малой эффективной массой носителя заряда m* и большим значением временем свободного пробега или точнее времени релаксации τ₀. В полупроводниках эффективная масса носителей заряда может быть как больше, так и меньше массы свободного электрона.

Время релаксации, характеризующее уменьшение тока после снятия поля, определяется процессами рассеяния движущихся в полупроводниках электронов. Чем больше частота столкновений и чем они интенсивнее, тем меньше время релаксации, а следовательно, и подвижность.

При комнатной температуре средняя скорость теплового движения свободных электронов  в невырожденном полупроводнике около 10⁵ м/с.

Причинами рассеяния носителей заряда в полупроводниках, по-разному влияющими на температурную зависимость подвижности, являются:

1.  тепловые колебания атомов или ионов кристаллической решетки;

2.  примеси в ионизированном или нейтральном состоянии;

3.  дефекты решетки (пустые узлы, искажения, вызванные атомами внедрения, дислокации, трещины, границы кристаллов и т.д.).

3.3 Концентрация собственных носителей

В полупроводнике при любой температуре в результате процессов тепловой генерации и рекомбинации устанавливается некоторая равновесная концентрация электронов n₀ и дырок p₀.

У собственных полупроводников:

 

n_i=p_i, n_i+p_i=2n_i (3.8)

Единица измерения концентрации – штук в единице объема.

Классическое распределение Больцмана для молекул газа в единице объема и статистика Максвелла – Больцмана, если Е_i – полная энергия частицы, дают следующую формулу для определения концентрации этих частиц:

(3.9)

В квантовой теории вероятность заполнения энергетического уровня электронами подчиняется статистике Ферми-Дирака и определяется функцией Ферми:

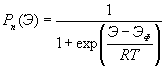(3.10)

где Э – энергия уровня, вероятность заполнения которого определяется T – температура, k=1.3810^-23 (Дж/К) = 0.8610^-4 (Эв/К) – постоянная Больцмана.

Э_ф – энергия уровня Ферми, вероятность заполнения которого равна 0.5 и относительно которого кривая вероятности симметрична.

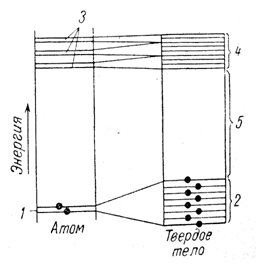
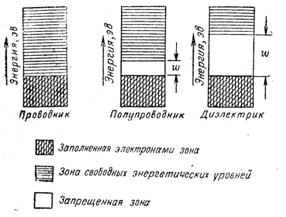
Для полупроводников:

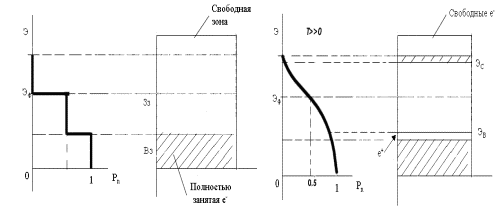
Рисунок 3.1 – Положение энергетических зон в полупроводнике

При Т=0⁰К функция Ферми обладает следующими свойствами:

P_n(Э)=1 если Э<Э_ф

P_n(Э)=0 если Э>Э_ф

Величина Э_ф – уровень Ферми [Эв] [Дж] или энергия электрохимического потенциала

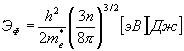 (3.11)

где n – концентрация электронов валентной зоны.

В системах частиц, описываемых антисимметричными волновыми функциями, осуществляется распределение Ферми-Дирака. Этой статистикой описывается поведение систем фермионов (электронов, протонов, нейтронов) частиц, подчиняющихся принципу Паули и имеющих полуцелый спин (± 1/2).

Находясь на уровне Э_ф при T=0⁰К электрон обладает максимальной энергией.

Таким образом величина Э_ф определяет максимальное значение энергии, которую может иметь электрон в твердом теле при температуре абсолютного нуля, т.е. при T=0⁰К в металле нет электронов с энергией > Э_ф. То есть энергия уровня Ферми соответствует верхней границе электронного распределения при T=0⁰К, а также средней энергии «диапазона размытия» при любой другой температуре. Энергия Ферми или энергия электрохимического потенциала – работа, которую необходимо затратить для изменения числа частиц в системе на единицу при условии постоянства объема и температуры.

Симметрия кривой вероятности заполнения относительно уровня Ферми означает одинаковую вероятность заполнения уровня электроном с энергией, большей на величину Э-Э_ф, и вероятность освобождения уровня от электрона с энергией на столько же меньшей энергии уровня Ферми.

Потенциал φ_ф, соответствующий уровню Э_ф

φ_ф=Э_ф/е [Дж / Кл] (3.13)

где e=1.6*10^-19 (Кл) – заряд электрона.

Электроны в статистике Ферми-Дирака неразличимы. Статистика Ферми-Дирака справедлива для частиц с полуцелым спином, которые называются фермионами.

С помощью функции Ферми можно определять заполнение электронами зоны проводимости или валентной зоны полупроводника. Для валентной зоны удобнее говорить о дырках – пустых энергетических уровнях в валентной зоне.

Любой энергетический уровень может либо занят электроном, либо свободен от электрона (занят дыркой). Поэтому сумма вероятностей

 

P_n(Э)+P_p(Э)=1 (3.14)

Тогда вероятность заполнения энергетического уровня дыркой

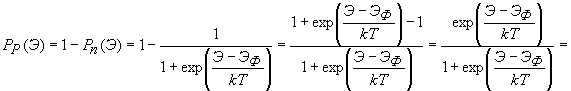
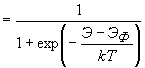
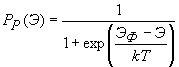 (3.15)

Как видно из последнего выражения функция вероятности для дырок совершенно аналогична функции вероятности для электронов. Различие состоит в том, что для дырок энергия возрастает при движении вниз от уровня Ферми, т.е. чем «глубже» находится дырка, тем дольше ее энергия.

Уровень Ферми обычно расположен в запрещенной зоне энергетической диаграммы относительно далеко (в единицах энергии) от зоны проводимости и от валентной зоны по сравнению с энергией (энергия, сообщаемая кристаллу при нагревании, при комнатной температуре kT0.025ЭВ).

Поэтому, пренебрегая единицей в знаменателе функции Ферми вероятность распределения электронов по энергетическим уровням зоны проводимости может определяться уже не квантовым распределением Ферми-Дирака, а классической статистикой Максвелла – Больцмана:

 (3.16)

Однако нужно иметь ввиду, что в микросистемах у которых N – число частиц,

 (3.17)

а G‑число возможных состояний для них, когда вероятность заполнения всех возможных состояний 1, т.е. при N/G1 наступает «вырожденность».

Если же, N/G<<1, то это невырожденная система.

Системы микрочастиц в металлах, поведение которых описывается статистикой Ферми-Дирака, являются вырожденными. В состоянии вырождения средняя энергия электронного газа (металлическая связь) практически не зависит от температуры.

Электронный газ в металле остается выраженным до тех пор, пока любой из электронов не сможет обмениваться энергией с кристаллической решеткой, а это, а свою очередь, возможно лишь тогда, когда средняя энергия тепловых колебаний станет близкой к энергии уровня Ферми.

В отличие от металлов электронный газ у большинства полупроводников является невыраженным, т. к. у них в зоне проводимости много свободных состояний, а для невырожденных полупроводников (их большинство) можно пользоваться статистикой Максвелла-Больцмана и только в некоторых случаях для вырожденных полупроводников необходимо использовать статистику Ферми-Дирака.

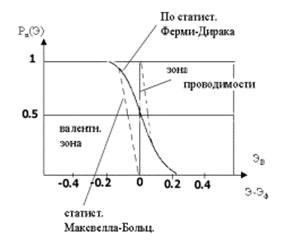
Рисунок 3.2 – Разница в двух функциях распределения электронов по энергиям

Вывод

В данной курсовой работе были рассмотрены полупроводниковые материалы кремний и германий. Описаны основные сведения о кристаллическом строении, процессах получения, физико-химических и электрофизических свойствах, применении в полупроводниковых приборах и ИС. Следует сказать, что техника получения монокристаллов германия высокой чистоты разработана в настоящее время достаточно надежно и обеспечивает выпуск монокристаллического германия в промышленном масштабе. Требования к свойствам материалов по мере развития техники непрерывно растут, причём подчас необходимо получить труднореализуемые либо даже несовместимые сочетания свойств.

Были проанализированы температурные зависимости концентрации, подвижностей носителей заряда в полупроводниках, а также охарактеризованы методы контроля полупроводниковых материалов.

 

Список использованной литературы

1.  Пасынков В.В., Сорокин В.С. Материалы электронной техники – М.: Высш. шк., 1986.

2.  Н.И. Слипченко, В.А. Антонова, О.В. Бородин, Ю.О. Гордиенко. Материалы электронной техники. Учеб. пособие – Х.: ХТУРЭ, 2001.

3.  Бонч-Бруевич В.Л, Калашников С.Г. Физика полупроводников. – М.: Наука, 1977

4.  Пасынков В.В., Чиркин Л.К. Полупроводниковые приборы. М.: Высшая школа, 1987.

5.  Сайт интернета http://www.techno.edu.ru

6.  Методичні вказівки до курсової работи студентів з дисципліни «Матеріали електронної техніки»/ Упоряд.: М.І. Сліпченко, О.М. Рибін – Харків: ХНУРЕ, 2005.

7.  Богородицкий Н.П., Пасынков В.В., Тареев Б.М. Электротехнические материалы. – Л.: Энергоатомиздат, 1985.

8.  Воробьев Ю.В., Добровольский В.Н., Стриха В.И. Методы исследования полупроводников. – Киев: Высш. шк., 1988.