Типові системи радіоавтоматики

3. Типові системи радіоавтоматики

На практиці найчастіше використовуються такі типи систем РА: системи автоматичного визначення напрямку на джерело радіохвиль (системи АСН), системи автоматичного спостереження за частотою і фазою радіосигналу (системи АПЧ і ФАП), системи автоматичного спостереження за часовим положенням одного або кількох радіо- і відеоімпульсів (системи АСД), системи автоматичного регулювання підсилення (системи АРП).

Системи АСН поширені у радіолокації, радіонавігації, радіокеруванні. Вони призначені для виміру кутових координат об'єктів, що рухаються, і спостереження за їх просторовим положенням.

Системи АПЧ застосовуються у радіоприймальних пристроях з метою підтримки постійної проміжної частоти сигналу і як демодулятори частотно-модульованих коливань. Також системи АПЧ використовуються для стабілізації частоти коливань, що генеруються і як вузькосмугові фільтри, які перебудовуються по частоті. Системи ФАП використовуються для тих самих цілей, що й АПЧ, але відрізняються тим, що забезпечують підстроювання не тільки по частоті, але й по фазі коливань, тобто є чутливішими і точнішими системами.

Системи АСД широко застосовуються у радіолокації і радіонавігації для виміру дальності до обраної цілі і спостереження за її радіальними переміщеннями у просторі. Також ці системи здійснюють просторово-часову селекції декількох об'єктів.

Системи АРП застосовуються у радіоприймальних пристроях різних видів для стабілізації рівня сигналу на виході підсилювачів при великому динамічному діапазоні вхідного сигналу.

 

4. Математичний опис автоматичних систем

Будь-яка система радіоавтоматики (РА) складається з ряду елементів (ланок). Для кожного елемента характерний зв'язок між його входом і виходом. Він виражається диференціальним рівнянням. Система РА описується системою диференціальних рівнянь.

4.1 Складання диференціального рівняння елемента автоматичної системи

Конкретний вид диференціального рівняння залежить від фізичної природи і властивостей елемента.

Розглянемо як приклад інерційну RC- ланку (рис. 2):

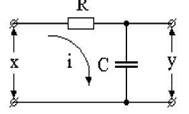
Рисунок 2 – Схема інерційної ланки

Якщо визначити х та y як відповідно вхідну і вихідну напруги цієї ланки, то згідно з теорією електричних кіл можна записати таке рівняння:

З урахуванням того, що

 

отримаємо таке рівняння:

Позначимо RC=T, тоді можна записати:

Уведемо до розгляду символ диференціювання за часом

 

Цей штучний (але по суті вірний) прийом дозволяє переписати отримане диференційне рівняння у формі:

Винесемо вихідну напругу y за дужки і остаточно отримаємо:

.

Відзначимо, що вираз

 

називається операторним коефіцієнтом передачі інерційної (у даному випадку) ланки.

 

4.2 Статичні і динамічні властивості елементів

Після подачі на вхід елемента деякого впливу на його виході виникає перехідний процес, по закінченні якого настає стаціонарний стан.

Статична характеристика - це залежність, що зв'язує між собою стаціонарні вхідну і вихідну величини.

Прикладом статичної характеристики може служити залежність між напругою на виході частотного дискримінатора і відхиленням частоти сигналу від його номінального значення (рис.3).

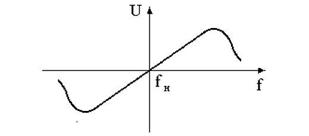
Рисунок 3 – Статична характеристика дискримінатора

Динамічна характеристика - це залежність, що зв'язує між собою зміни вхідної і вихідної величин у перехідному режимі.

 

4.3 Перетворення Лапласа

Перетворення Лапласа має дві взаємозалежні форми – пряму і зворотну.

Пряме перетворення описується так:

 ,

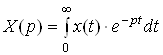де x(t) – оригінал функції, тобто функційна залежність у часовому вимірі;

x(p) – зображення функції x(t) за Лапласом, тобто у вимірі комплексної змінної

.

Зворотне перетворення вводиться у розгляд так:

,

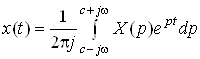що дозволяє відшукати оригінал функції x(t) по її зображенню X(p).

Існують такі методи відшукання оригіналу x(t): табличний та метод інтегрування у комплексній площині.

Глибинний сенс перетворення Лапласа полягає у тому, що за його допомогою стає можливим здійснити перехід від вихідних диференційних рівнянь, що описують систему РА у просторі комплексної змінної р .

На рис. 4 наведено загальну структурну схему ланки системи РА, яка описується коефіцієнтом передачі R(p). На цьому рисунку G(p) та x(p) – відповідно сигнали у операторній формі на вході і виході ланки.

Рисунок 4 – Загальна структурна схема ланки системи РА з коефіцієнтом передачі R(p) у операторній формі.

Наприклад, якщо ланка є диференціатором, то R(p)=p.

Тоді  Якщо ланка є інтегратором, то

Тоді

4.4 Перетворення Фур'є

Якщо в перетворенні Лапласа замінити оператор р на змінну jw отримаємо перетворення Фур'є, яке також поділяється на пряме та зворотне.

Для прямого перетворення Фур'є маємо вираз

,

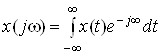де x(jω) – спектральна функція дії x(t).

Зворотне перетворення Фур'є має вид:

.

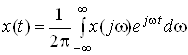4.5 Передатна функція

Передатною функцією N(s) елемента (системи) РА називається відношення зображення вихідної величини елемента (системи) Y(s) до зображення ) вхідної величини X(s) при нульових початкових умовах

Формально передатну функцію отримуємо з диференціального рівняння елемента (системи) РА у символічній формі шляхом заміни в ньому символу р на комплексну змінну s і розділення утвореного в такий спосіб багаточлена правої частини рівняння на многочлен лівої частини.

Наприклад, якщо диференціальне рівняння інерційного RC- елемента має вигляд.

;

звідки

.

Тоді

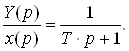
Тепер при виконанні заміни оператора p на комплексну змінну S отримаємо:

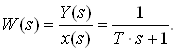
У цьому виразі комплексні величини x(s) і Y(s) є зображенням за Лапласом часових величин x(t) і y(t).

4.6 Перехід від передатної функції до частотної характеристики

У загальному виді передатна функція записується так:

,

де Q(s) - багаточлен у чисельнику, P(s) – багаточлен у знаменнику, к – постійний множник.

Замінимо комплексну перемінну s на комплексну частоту jw - одержимо амплітудно-фазо-частотну характеристику елемента (системи):

 .

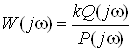Наприклад, передатна функція послідовного з'єднання безінерційного підсилювача з коефіцієнтом підсилення к-го інерційного RС- ланцюга має вигляд

 .

Замінимо s на jw:

 

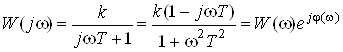
це модуль комплексного виразу, або ж, амплітудо-частотна характеристика даного елемента;

 

- це аргумент комплексного виразу, або ж, фазочастотна характеристика елемента.

Запишемо W(jw) в алгебраїчній формі:

.

Тут U(w) – реальна частотна характеристика. V(w) - уявна частотна характеристика.

У випадку замкнутої системи РА передатна функція позначається через Ф(s),а амплітудно-фазо-частотна характеристика – через

,

де P(w) і Q(w) – відповідно реальна і уявна частотні характеристики замкнутої системи.

4.7 Логарифмічні частотні характеристики

У реальних автоматичних системах модуль частотної характеристики змінюється в дуже широких межах при зміні частоти. Тому графічне зображення їх у звичайному масштабі неможливо. У цих випадках зручно скористатися логарифмічними частотними характеристиками: амплітудною і фазовою.

Логарифмічна амплітудно-частотна характеристика визначається співвідношенням

,

де L(w) – у децибелах, а частота w відкладається в декадах чи октавах. Логарифмічна фазо-частотна характеристика f(w) відображається в градусах, а частота – у декадах чи в октавах (рис.5).

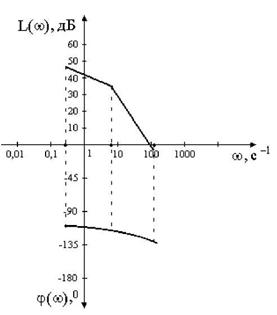
Рисунок 5 – Логарифмічні амплітудно-фазо-частотні характеристики