Навигация
Проектирование двухстепенного манипулятора с самонастройкой
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Контрольная работа
по курсу «Проектирование автоматических систем»
Проектирование двухстепенного манипулятора с самонастройкой
Выполнила: Губарева О.Е.
Заочная форма обучения
Курс V
Специальность 210100
№ зачетной книжки 607932
Проверил преподаватель: Воронин Ю.Ю.
Москва 2010 г.
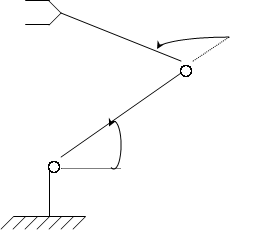
1. Уравнение динамики исполнительного механизма двухстепенного манипулятора
|
|
|
|
Параметры манипулятора для 2-го варианта
М1,(кг)= 10
М2,(кг)=15
l1,(м)=1,8
l1,(м)=3
Входными сигналами манипулятора служат управляющее напряжение на приводе. Выходными сигналами служат обобщенные координаты q.
М1, М2 – масса первого и второго звена;
l1, l2 – длины приводов.
Динамика данного исполнительного механизма описывается уравнением:
А(q)![]() + B(q,
+ B(q,![]() ) + G(q) =
) + G(q) = ![]() [H•м]
[H•м]
q = ![]() - обобщенные координаты манипулятора;
- обобщенные координаты манипулятора;
![]() =
= ![]() - управление (момент нагрузки приводов всех подвижностей).
- управление (момент нагрузки приводов всех подвижностей).
А(q) – матрица инерции (2×2);
G(q) – матрица гравитационных сил;
B(q,![]() ) – матрица моментов скоростных сил;
) – матрица моментов скоростных сил;
![]() - ускорение ротора.
- ускорение ротора.
B(q,![]() ) =
) = ![]()
![]()
B1(q) и B2(q) – симметричные матрицы 2×2;
G(q) – моменты гравитационных сил (сил тяжести).
Выражения для матриц1. Для матрицы А(q) = ![]() , где
, где
Элемент А11 определяет момент инерции нагрузки на первый привод манипулятора
А11 = Н1+Н2+Н3+М2 · l1 ·l2 · Cos q2, где
Н1 = ![]()
Н1 = (10 · 1,82 )/4= 8,1
Н2 = М2 l12
Н2 = 15 · 1,82 = 48,6
Н3 = ![]()
Н3 = (15 · 32 ) / 4 = 33,75
А11 = 8,1 + 48,6 + 33,75 + 15 ·1,8 ·3 · Cos q2 = 90,45 + 81 Cos q2
А12 = А21 = Н3 + ½М2 l1 l2 Cosq2 – определяют взаимовлияние друг на друга двух степеней подвижности.
А12 = А21 = 33,75 + ½(15 · 1,8 · 3) · Cos q2 = 33,75 +40,5 Cos q2
А22 = Н3 – определяет момент инерции на второй привод;
А22 = 33,75
А(q) = ![]()
2. Для матрицы B1(q) и B2(q):
B1(q) = ![]() ,
,
где
![]() = -½ М2 l1 l2 Sin q2
= -½ М2 l1 l2 Sin q2
![]()
![]() =
= ![]() = - ½ (15 ·1,8 ·3) Sin q2 = - 40,5 Sin q2
= - ½ (15 ·1,8 ·3) Sin q2 = - 40,5 Sin q2
B1(q) = ![]() ,
,
B2(q) = ![]() ,
,
![]() = ½ М2 l1 l2 Sinq2
= ½ М2 l1 l2 Sinq2
![]() = 40,5 Sin q2
= 40,5 Sin q2
B2(q) = ![]()
При расчете управления потребуются собственные числа:
![]() матриц В1(q) и В2(q). Эти матрицы симметричные.
матриц В1(q) и В2(q). Эти матрицы симметричные.
Собственные числа ![]() находят из уравнения:
находят из уравнения:
det ![]() = 0
= 0
B1(q) - ![]() E =
E = ![]() -
- ![]()
![]() =
=
![]() -
-
- 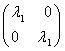 =
= 
![]()
![]() =
= 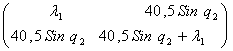
det ![]() =
= 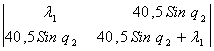 =
= ![]() (40,5 Sin q2 +
(40,5 Sin q2 + ![]() ) –
) –
1640,25 Sin2q2 = ![]() +40,5 Sinq2
+40,5 Sinq2![]() - 1640,25 Sin2q2
- 1640,25 Sin2q2
Решим уравнение:
![]() +40,5 Sinq2
+40,5 Sinq2![]() - 1640,25 Sin2q2 = 0
- 1640,25 Sin2q2 = 0
![]() = 25 Sinq2
= 25 Sinq2
![]() = -65,5 Sinq2
= -65,5 Sinq2
Таким образом найдены собственные числа для матрицы В1(q).
B2(q) - ![]() E =
E = ![]() -
- ![]()
![]() =
= ![]() -
- 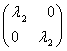 =
=
![]()
![]() =
= ![]()
det ![]() =
= 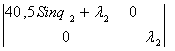 =
= ![]() (40,5 Sinq2 +
(40,5 Sinq2 + ![]() )
)
![]() (40,5Sinq2 +
(40,5Sinq2 + ![]() ) = 0
) = 0
40,5 Sinq2 + ![]()
![]() = - 40,5 Sinq2
= - 40,5 Sinq2
![]() = 0
= 0
![]() = - 40,5 Sinq2
= - 40,5 Sinq2
Таким образом найдены собственные числа для матрицы В2(q).
Для моментов всех тяжестей матрица моментов гравитационных сил G(q):
а) для первого привода:
G1(q) = ![]() - момент тяжести для первого привода
- момент тяжести для первого привода
G1(q) = ![]()
=352,8·Cosq1+220,5·Cos(q1+q2)
G2(q) = ![]() = 220,5Cos (q1 + q2)
= 220,5Cos (q1 + q2)
Выразим частные производные:
![]()
![]()
![]()
![]()
0 комментариев