Определение удельного сопротивления эпитаксиального слоя

2. Определение удельного сопротивления эпитаксиального слоя

Величина удельного сопротивления эпитаксиального слоя (ЭС) определяется с учетом заданного значения пробивного напряжения V_КБ.

Известно [1], что величина пробивного напряжения плоского резкого p-n-перехода определяется следующим соотношением:

, (2.1)

где N_ЭС – концентрация примеси в ЭС, в котором формируется p-n-переход коллектор–база.

Для планарного p-n-перехода справедливо следующее выражение [1]:

, (2.2)

где U_{пр.плоск.} – пробивное напряжение плоского p-n-перехода; n = 1 для цилиндрического и n = 2 для сферического p-n-перехода.

, (2.3)

где r – радиус кривизны p-n-перехода, равный глубине залегания этого p-n-перехода; W₀ – ширина области объемного заряда (ООЗ) резкого p-n-перехода при напряжении пробоя плоского p-n-перехода:

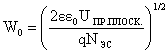. (2.4)

Проведем расчет для случая сферического p-n-перехода, т.е. n = 2.

Зададим значение глубины залегания p-n-перехода x_jК-Б = 3 мкм, тогда r = x_jК-Б =3 мкм.

Зададим приблизительное значение N_ЭС. Для этого воспользуемся графиком зависимости напряжения лавинного пробоя p-n-перехода с различной геометрией переходов рис. 9.3 [1]: N_ЭС(15 В) = 5_*10¹⁶ см^-3.

Используя полученное из графика значение N_ЭС, рассчитаем пробивное напряжение плоского p-n-перехода. Согласно формуле (2.1):

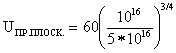= 17,944 В.

Определяем величину W₀ в соответствии с (2.4):

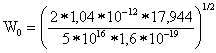= 6,826_*10^-5 см = 0,6826 мкм.

Находим

.

По формуле (2.2) определяем точное значение пробивного напряжения p-n-перехода коллектор–база при N_ЭС = 5_*10¹⁶ см^-3:

U_{пр.план.} = 17,944_*{[(2+1+4,395) _*4,395²]^1/3-4,395} = 14,937 В.

Сравниваем полученное нами точное значение пробивного напряжения (14,937 В), с заданным в задании на курсовой проект значением пробивного напряжением коллектор–база (15 В). Отмечаем, что разница не превышает 10%. Поэтому оставляем выбранное нами значение концентрации эпитаксиального слоя N_ЭС = 5_*10¹⁶ см^-3. С помощью рис. 6.4 [1] найдем удельное сопротивление ЭС _ЭС = 0,4 Ом_*см.

3. Определение толщины эпитаксиального слоя

Толщина ЭС определяется исходя из соотношения:

h_ЭСmin = x_jК-Б+W₀+сс, (3.1)

где x_jК-Б – глубина залегания p-n-перехода коллектор–база; W₀ – ширина ООЗ p-n-перехода при рабочем напряжении (напряжении пробоя); сс – величина расплывания СС в ЭС, отсчитываемая от границы раздела подложка–ЭС. Зададим глубину залегания x_jК-Б = 3 мкм и величину расплывания сс = 3 мкм.

Определим ширину ООЗ p-n-перехода по формуле (2.4)

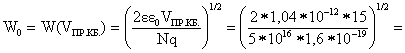 6,241_*10^-5 см = 0,624 мкм.

Согласно (3.1) толщина ЭС h_ЭС будет равна:

4. Определение режимов эпитаксии

Температура эпитаксии обычно равна 11501200 ⁰С. Зададим температуру эпитаксии Т_Э=1150 ⁰С.

Скорость наращивания ЭС соответствует диапазону v_ЭН = 0,10,3 мкм/мин. Выбираем v_ЭН = 0,2 мкм/мин.

Следовательно, длительность эпитаксиального наращивания:

5. Определение режимов разделительной диффузии

Разделительные дорожки (РД) формируются путем диффузии бора В⁺ с поверхности ЭС вглубь до смыкания с подложкой. При этом глубина залегания РД должна быть меньше ЭС на 1 мкм, т.е.

x_jРD = h_ЭС + 1 мкм. (5.1)

В нашем случае, согласно выражению (5.1) x_jРD = 7,062 мкм.

Глубина разделительной диффузии описывается следующим выражением:

, (5.2)

где D₂t₂ – параметры второй стадии разделительной диффузии; N₀ – концентрация на поверхности диффузионного разделительного слоя; N_П = N_ЭС – концентрация примеси в ЭС.

В формуле (5.2) должно выполняться соотношение: N₀10³N_П. (5.3)

Положим, что N₀ = 10³N_П = 10³N_ЭС = 5_*10¹⁹ см^-3. Из выражения (5.2) определяем D₂t₂:

.

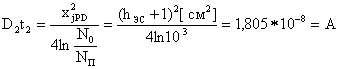Задаем температуру второй стадии диффузии: Т₂=1220 ⁰С. Определим D₂. Пользуясь рис. 9.5, а [1] находим, что для Т₂ = 1220 ⁰С коэффициент диффузии бора D₂(1220) = 3,5_*10^-12 см²/c.

Рассчитываем значение t₂:

Определяем параметры первой стадии разделительной диффузии. Распределение примеси после второй стадии диффузии описывает выражение:

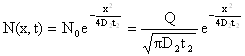, (5.4)

где Q – количество примеси, введенное в полупроводник на первой стадии диффузии. Оно определяется через параметры первой стадии диффузии выражением:

, (5.5)

где N₀₁ – величина предельной растворимости. Определяется по графику (рис.9.5, а) [1].

Подставим выражение (5.5) в (5.4), и выразим N₀:

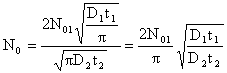, (5.6)

где N₀, согласно (5.3), принимаем равным N₀ = 10³N_ЭС = 5_*10¹⁹ см^-3.

Из (5.6) выражаем D₁t₁:

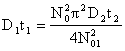. (5.7)

Зададим температуру первой стадии диффузии: Т₁=1150 ⁰С. По графику зависимости рис. 9.5, а [1] находим: D₁(1150 ⁰C) = 7_*10^-13 см²/c.

С помощью рис. 5.2 [1] находим предельную растворимость бора в кремнии N₀₁(T₁) = N₀₁(1150 ⁰C) = 5,4_*10²⁰ см^-3.

Определяем t₁ из выражения (5.7):

В результате получаем следующее распределение примеси в разделительных дорожках:

.