Навигация
Электрический и конструктивный расчет
3. Электрический и конструктивный расчет
3.1 Расчет резистивного элемента
Определим ток, протекающий через наш резистивный элемент, по формуле [1]:
![]() (3.1.1)
(3.1.1)
где I – ток, А; Р – мощность, Вт; R – сопротивление, Ом.
![]()
Зная ток, определим диаметр проволоки по формуле [1]:
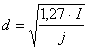 (3.1.2)
(3.1.2)
j - плотность тока выбираем ,учитывая условия температурной стабильности и малые габаритные размеры будущего резистора j=1.8![]() ,так как проектируемый резистор должен быть достаточно маломощным ,а также сила тока I=26мА - довольно небольшая величина. Из конструктивных соображений диаметр провода резистивного элемента выбираем d=0.15мм.
,так как проектируемый резистор должен быть достаточно маломощным ,а также сила тока I=26мА - довольно небольшая величина. Из конструктивных соображений диаметр провода резистивного элемента выбираем d=0.15мм.
![]()
При таком диаметре проволоки ее длина должна равняться:
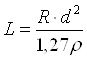 , (3.1.3)
, (3.1.3)
![]() где ρ –удельное электрическое сопративление, Ом·мм2/м, для Манганина составляет 0,5 Ом·мм2/м
где ρ –удельное электрическое сопративление, Ом·мм2/м, для Манганина составляет 0,5 Ом·мм2/м
![]()
Выбираем размеры каркаса:
D=3…5 См
![]()
Для обеспечения требуемой разрешающей способности =0,01%,D=0.5мм,![]()
Определяем полезную длину намотки по формуле:
B=0.85![]() ;
; ![]()
B=0.85![]()
Количество витков, которое можно разместить на этой длине, определяется по формуле:
![]() ;
; ![]()
N=![]() ,
,
где ![]() шаг намотки ,он равен
шаг намотки ,он равен ![]() d=
d=![]()
![]() коэффициент численно равный шагу намотки к диаметру провода.
коэффициент численно равный шагу намотки к диаметру провода.
Разрешающая способность проектируемого резистора определяем по формуле:
![]() ;
; ![]() ,
,
где N- количество витков
![]() =0,011%
=0,011%
Это соответствует заданной разрешающей способности.
Площадь поверхности резистивного элемента определяем по формуле:
![]() ;
; ![]() ,
,
где d-диаметр провода=0,15мм
R-сопротивление проектируемого резистора=900Ом
![]()
Определяем ширину каркаса при помощи расчета:
Так как проектируемый резистор должен обладать логарифмической функциональной характеристикой ,то ширина каркаса будет не одинаковой и поэтому необходимо с начало рассчитать по какому закону будет изменяться ширина каркаса:
![]() ;
; ![]() ,
,
где ![]() значение высот каркаса(каркас мы разбиваем на прямоугольники ,высоты которых изменяются по логарифмическому закону. Количество таких прямоугольников выбираем равным 8.Из конструктивных соображений
значение высот каркаса(каркас мы разбиваем на прямоугольники ,высоты которых изменяются по логарифмическому закону. Количество таких прямоугольников выбираем равным 8.Из конструктивных соображений ![]() ,а
,а ![]()
![]() -определяем по формуле:
-определяем по формуле:
![]() ;
; ![]() ,
,
где ![]() угол укладки провода на каркас .При использовании данного провода
угол укладки провода на каркас .При использовании данного провода ![]()
![]() Коэффициент учитывающий особенности изгиба проволоки на каркас, берём равным 1,05.
Коэффициент учитывающий особенности изгиба проволоки на каркас, берём равным 1,05.

Тогда:
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;
Похожие работы
... расчета гребного винта. Во всех схемах расчёта очень часто используются результаты продувок изолированных профилей в аэродинамических трубах. Во многих схемах расчёта используется вихревая теория гребных винтов. При проектировании гребных винтов в основном решается одна из двух задач: а.) В результате проектирования устанавливаются элементы гребного винта обеспечивающие наивысшую скорость судна. ...
... Uн=110кВ нет возможности обеспечить всех потребителей нужным качеством ЭЭ. 8. Определение потерь мощности в районной сети при Uн=220кВ Определение потерь мощности в максимальном режиме По табл. 5.1 рассчитаем сопротивления линий и результаты сведём в табл. 8.1 Таблица 8.1. Результаты расчётов сопротивлений участков сети Участок сети r, Ом x, Ом b×10-6, См Aa 18,15 ...
... меры к его понижению (забивка дополнительных электродов и т.д.). Глава 7. РАСЧЁТ ПОКАЗАТЕЛЕЙ ЭКОНОМИЧСЕКОЙ ЭФФЕКТИВНОСТИ ПРОЕКТА В данной главе рассмотрим вопросы капиталовложений при реконструкции подстанции, расчет эксплуатационных затрат при проведении текущих ремонтов и технических обслуживаний, определение затрат на потреблённую электроэнергию, расчет экономических показателей при ...
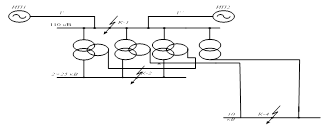
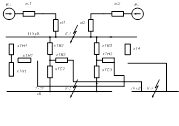
... состояния: от каждого источника до места к.з. одно результирующее сопротивление. По расчётной рисунок и электрической схемах замещения (рис.6) находим относительные сопротивления энергосистемы до шин подстанции: , (3.3.1) , (3.3.2) где Sб – базисная мощность, МВА; Sкз1,2 – мощность трёхфазного к.з. каждой системы, МВА. Расчёт относительного сопротивления энергосистемы до шин ...


0 комментариев