АНАЛІЗ СТАТИСТИЧНИХ ХАРАКТЕРИСТИК І ПАРАМЕТРІВ ПЕРЕДАВАЄМОГО ПОВІДОМЛЕННЯ

2. АНАЛІЗ СТАТИСТИЧНИХ ХАРАКТЕРИСТИК І ПАРАМЕТРІВ ПЕРЕДАВАЄМОГО ПОВІДОМЛЕННЯ

За умовою курсової роботи вихідне безперервне повідомлення  являє (зображає) собою стаціонарний гаусовский випадковій процес з нульовим математичним чеканням ( , де М – знак статистичного усереднення по безлічі реалізації), потужність  і функція кореляції  якого задані в табл. 1.

Гаусовский (нормальний) випадковий процес у будь - який момент часу характеризується одномірної ФПВ наступного (такого) виду:

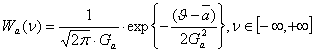(2.1)

В часовій і спектральній областях стаціонарний випадковий процес визначається, відповідно, функцією кореляції  і спектральній щільності потужності чи енергетичним спектром , де . . Ці характеристики зв'язані парою перетворень Вінера - Хінчина:

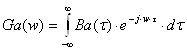(2.2)

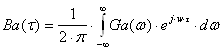(2.3)

Враховуючи, що для стаціонарного випадкового процесу обидві ці функції дійсні і парні, тоді відношення (2.2 і 2.3) можливо записати у такому вигляді:

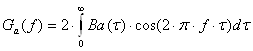(2.4)

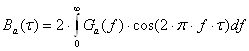(2.5)

Функція кореляції згідно з вихідними даними має такий вигляд:

 (2.6)

Тепер підставимо відомі величини у формулу (2.6)

 (2.7)

По (2.7) побудуємо графік функції кореляції:

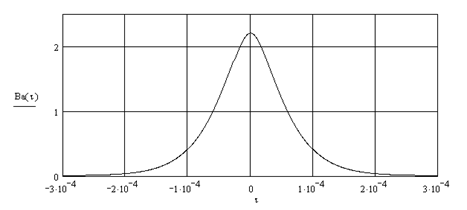
Рис. 2.1 – Функція кореляції

Тепер згідно (2.4) розрахуємо спектр щільності потужності повідомлення:

(2.8)

Побудуємо графік спектра щільності потужності повідомлення згідно з виразом (2.8)

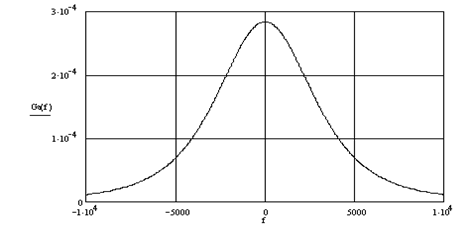
Рис. 2.2 – Спектр щільності потужності повідомлення

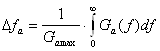По функції  знаходимо енергетичну ширину спектра , за формулою (2.9):

 (2.9)

де  - максимальне значення енергетичного спектру.

Ширина спектра - це область частот, у якій зосереджена основна частка енергії повідомлення (сигналу); інтервал кореляції це - проміжок часу між перетинами випадкового процесу, у межах якого ще спостерігається їхній взаємозв'язок (кореляція), при - цим взаємозв'язком (кореляцією) зневажають.

(2.10)

По функції кореляції Ва(t) знайдемо інтервал кореляції t_к по формулі:

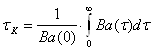(2.11)

Тепер підставимо відомі величини у формулу (2.11) і вичислимо :

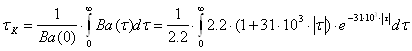(2.12)

Вихідне повідомлення перед його аналого-цифровим перетворенням пропускається через ідеальний ФНЧ. Фільтрація - це лінійне перетворення.-Тому відгук  ФНЧ на гаусовский вплив буде також гаусовским випадковим процесом з нульовим математичним чеканням  і потужністю, обумовленої зі співвідношення:

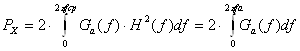(2.13)

Потужність відгуку розраховуємо по формулі:

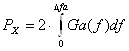(2.14)

Тепер підставимо відомі величини у формулу (2.14) і вичислимо :

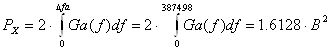(2.15)

Тут враховано, що амплітудно-частотна характеристика ідеального ФНЧ дорівнює одиниці в смузі частот  і нулю поза цією смугою. Крім того, його смуга пропущення  прийнята рівній енергетичній ширині спектра повідомлення , де  і  відповідно, нижня і верхня частоти, що для умов домашнього завдання рівні ,  . Звідси частота зрізу ИФНЧ дорівнює  . Це говорить про те, що відгук ИФНЧ є обмеженим по спектрі повідомленням. У ньому не містяться складові вихідного повідомлення на частотах . Кількісно ці втрати при фільтрації повідомлення характеризують середньо квадратичну похибкою (СКП):

Середньо квадратичну похибку знайдемо по формулі:

(2.16)

 (2.17)

Дане значення похибки фільтрації перевищує допустиме значення загальної похибки d_доп. Для його зменшення збільшимо енергетичну ширину спектра –  Гц. Тоді:

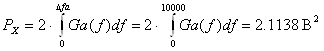(2.18)

(2.19)

(2.20)