Оптимальный когерентный прием дискретных сигналов и его помехоустойчивость

2 Оптимальный когерентный прием дискретных сигналов и его помехоустойчивость

 

В задаче распознавания сигналов, не содержащих случайных параметров(т.е. точно известных), «причинами» являются поступающие на вход сигналы , вероятности которых равны, очевидно, вероятности появления соответствующих элементов . «Следствиями» являются реализации суммы сигнала и помехи.

Количественно описание ситуации удобно производить с помощью рассмотрения векторов соответствующих колебаний. Вместо сигналов  будем оперировать однозначно соответствующими им векторами , а вместо реализаций y(t) – векторами , координаты которых определяются выражением, которое в нашем случае запишем так:

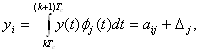(1)

В соответствии с теоремой Байеса

(2)

Как было отмечено, решение обычно выносится в пользу сигнала, имеющего наибольшую апостериорную вероятность. Так как знаменатель не зависит от номера I, то решающее правило(алгоритм решения) определяется так:

(3)

Следует обратить внимание на то, что в этих выражениях -- плотности вероятностей, так как компоненты вектора y, как видно из (1), являются непрерывными случайными величинами.

В выражении (3) априорные вероятности  передачи элементов  должны быть заданы. Следовательно, необходимо определить только правдоподобия . Это можно сделать исходя из того, что помеха аддитивна. Так как

,

то плотность вероятности некоторого значения вектора  равна плотности вероятности, что вектор помехи n примет значение . Отсюда следует, что если- известная нам плотность вероятности вектора помехи, то

(4)

Последний переход справедлив потому, что сигнал и помехи – независимые процессы.

Для дальнейшей конкретизации алгоритма необходимо задать определенный вид помехи. В большинстве случаев имеют место нормальные (гауссовские) или близкие к ним помехи. Вычисления в этом случае оказываются наиболее простыми. При гауссовских помехах каждая компонента вектора  распределена по нормальному закону

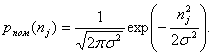(5)

В ряде случаев, в частности, при равномерном распределении энергии помехи по полосе рассматриваемых частот, компоненты вектора  являются независимыми случайными величинами. Тогда, как известно,

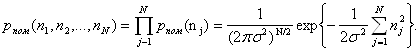(6)

При зависимых компонентах  выражение для  существенно усложняется и этот случай здесь рассматривать не будем.

Отметим, что ,т.е. является квадратом длины(нормы) вектора помехи.

Следовательно,

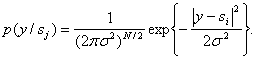 (7)

Отбросив множители, не зависящие от номера сигнала i, решающее правило(3) можно представить в виде

 (8)

Приемник, работающий по алгоритму(8), называется байесовским или приемником максимальной апостериорной вероятности. Если апостериорные вероятности элементов  одинаковы, то решающее правило упрощается:

 (9)

Соответствующий приемник называется приемником максимального правдоподобия. Правило(9) раскрывает механизм работы оптимального приемника.

Получив вектор y, с помощью обработки реализации y(t) необходимо вычислить расстояние от его конца до концов векторов всех возможных сигналов  и вынести решение в пользу того сигнала, для которого величина  будет минимальной, так как именно в этом случае функция (9) достигнет максимума. Коротко можно сказать, что оптимальный приемник выносит решение в пользу сигнала «ближайшего» к y(t).

Выражение(9) достигает максимума при минимуме показателя экспоненты. Следовательно, правило (9) можно записать в ином виде:

или, учитывая векторное представление

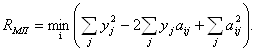(10)

Здесь первый член в скобках не зависит от номера i. Последний член – есть энергия i-того сигнала. Если энергии всех сигналов одинаковы, что обычно имеет место, то этот член также не зависит от номера i. Таким образом, решающее правило можно записать так:

(11)

Справедливость такого перехода обусловлена тем, что второй член в (10) имеет знак минус и выражение (10) минимизируется, если этот член достигает максимума. Выражение(11) уже позволяет определить структуру оптимального приемника. Однако удобнее это выражение представить в другом виде. Действительно, учтем, что

(12)

Тогда окончательно получим

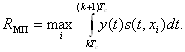(13)

Эта структура называется оптимальным корреляционным приемником, так как основная операция, лежащая в его основе, это операция корреляции y(t) со всеми возможными сигналами .

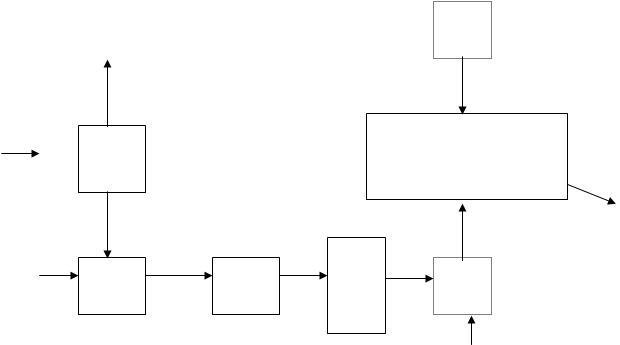
Из проведенного рассмотрения следует, что в состав оптимального приемника должны входить генераторы, вырабатывающие образцы сигналов, тождественные тем, которые используются на передатчике. Кроме того, между работой генераторов передатчика и приемника должна соблюдаться синхронность и синфазность, т.е. обеспечиваться идеальная синхронизация.