Навигация
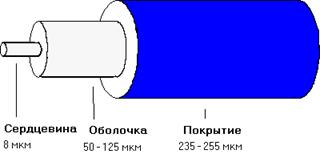
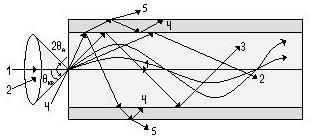
7 мкм. Анализ частных решений волнового уравнения (волноводных мод) показывает, что они описываются функциями, монотонно спадающими (обычно экспоненциально) к периферии сердечника, но в то же время не обрывающимися на границе сердечник оболочка (рис. 9.2). Иными словами, направляемые моды частично просачиваются в оболочку, т. е. отражение происходит не на геометрической поверхности раздела, а в некоторой приповерхностной области (рис. 9.2,а). Расчет показывает, что для направляемых мод с малыми углами падения (распространяющихся при малых значениях
доля мощности, переносимая по оболочке, может быть значительной: для 
моды приV =1 она составляет 70%, а при V=2,4 — всего 16%. Характерно и то, что при V= 1 поле
-моды проникает в оболочку на глубину порядка
Отсюда, в частности, следует важность чистоты не только сердечника, но и оболочки для маломодовых (и особенно одномодовых) волокон, а также необходимость достаточно большого диаметра оболочки 
Расчет дисперсии. Основное практическое приложение модовой теории - это расчет дисперсионных характеристик волокон различного типа. Наиболее наглядные выражения удается получить при анализе расплывания σ-импульса. Так, интегрированием решения волнового уравнения для многомодового двухслойного -ступенчатого световода получено
(9.9)
Используя переводное соотношение (9.1), получаем
что согласуется с качественными представлениями лучевой теории.
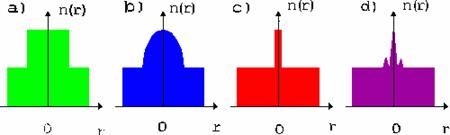
Дисперсия градиентного световода зависит от конкретного вида функции
Обычно при расчетах задаются следую щей формулой,
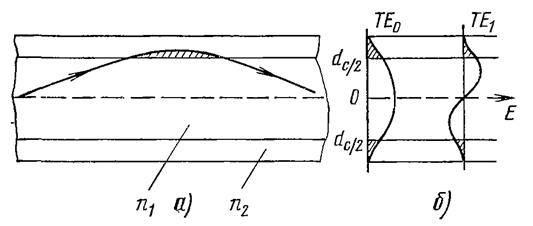
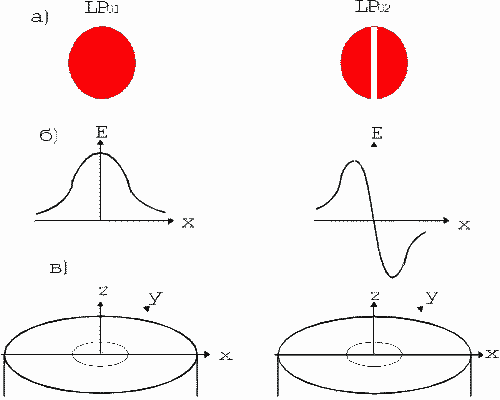
Рис. 9.2. «Просачивание» каналируемого излучения в оболочку:
а - модель лучевой теории; б — модовая структура поля для ТЕ0 и ТЕ1-мод
удовлетворительно описывающей практические все возможные типы существующих градиентных световодов:
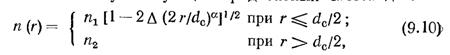
где
- относительная разность показателей преломления;
— постоянный для данного вида световода показатель, которым можно управлять технологически; 
- показатели преломления центра сердцевины и оболочки.
Для наиболее распространенного случая параболического изменения показателя преломления (при
когда (9.10) принимает вид
)
где
Детальные оценки показывают, что случай
не является оптимальным; наибольшее приближение к самофокусировке достигается при
При этом
Характерно, что для
градиентных световодов дисперсионные константы пропорциональны
, тогда как для волокон со ступенчатым профилем показателя преломления они пропорциональны; 
При условии 
становится очевидным преимущества градиентных волокон. Численные оценки по (9.9)—(9.13) показывают, что при
приведенное уширение импульса составляет 20 нс/км для двухслойного световода, 130 и 15 пс/км для градиентного параболического (
= 2) и оптимизированного' (
»1,97). Отсюда следует, в частности, что оптимизация достигается лишь при очень высокой точности реализации требуемого значения
Минимальные приведенные значения экспериментально получить не удается из-за дисперсии материала. Приведенная к единице длины постоянная времени материальной дисперсии приблизительно одинакова для всех волноводных мод и зависит лишь от ширины спектра излучения и дисперсионных свойств материала:
Используя (9.1), можно при необходимости перейти от
Экспериментальная дисперсионная кривая для кварца, легированного фосфором (материал сердечника практически всех основных типов световодов для ВОЛС), представленная на рис. 9.3,. показывает, что при λ≈3 мкм
=0 и соответственно 
= 0. Именно этим прежде всего и определяется значимость спектральной области вблизи λ =1,3 мкм.
Расчет показывает, что
в многомодовых световодах эффекты шнутримодовой дисперсии оказываются пренебрежимо малыми по сравнению с другими видами искажений и, в частности, с дисперсией материала. Поэтому, переходя к общей оценке, внутри-.модовую дисперсию не учитываем.
Рассмотренные эффекты — волноводная и материальная дисперсия — действуют одновременно; решение задачи уширения им-лульса при этом резко усложняется: наряду с членами, которые приводят к значениям
и 
появляется еще суперпозиционный член
. В первом приближении можно считать, что суммарное уширение импульса
Характерно, что
не соответствуют в точности значениям, получаемым из (9.11), (9.13), (9.14). Приведенные на рис. 9.4 расчетные кривые иллюстрируют сказанное и позволяют сделать следующие выводы: при учете двух механизмов дисперсии значение
заметно сдвигается относительно точки
, в градиентном световоде, возбуждаемом светодиодом, уширение импульса почти полностью определяется материальной дисперсией -и оптимизация профиля
заметных преимуществ не дает; в оптимизированном многомодовом градиентном световоде, возбуждаемом монохроматическим лазером, дисперсионное уширение .импульса может быть снижено до 15 пс/км (теоретический предел).
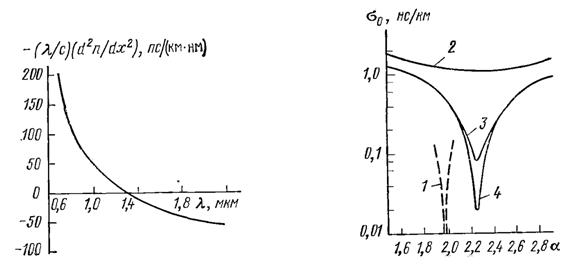
Рис. 9.3. Спектральная характеристика дисперсии кварца
Рис.9.4. Теоретическая зависимость 
от параметра 
градиентного световода:
1 — учитывается только модовая дисперсия; 2—
=15 нм (светодиод); 8 —
= 1 нм (инжекционный лазер); 4—
= 0,2 нм (лазер с распределенной обратной связью); кривые 2—4 рассчитаны для 
=0,9 мкм
Отметим еще один очень важный для дисперсионных расчетов эффект — связь мод в многомодовых световодах. Выше предполагалось, что отдельные моды (или лучи с разными углами падения) распространяются по волокну независимо друг •от друга и не смешиваются. Естественно, что идеализация и наличие в реальном световоде тех или иных нерегулярностей (флуктуации состава и соответственно величины п, непостоянства геометрии, микроизгибов, нарушений на границе раздела сердцевина— оболочка и т. п.) приводят к «перекачке» энергии между модами. В представлениях геометрической оптики это значит, -что луч с углом падения
преломившись на неоднородности, меняет угол распространения на 
Возможность проявления этого эффекта становится очевиднее, если вспомнить, что на 1 км пути укладывается около 109 длин волн света и в то же время происходит более 106 актов отражения светового луча от границы сердцевина — оболочка. Связь или смешение мод приводит ж тому, что часть энергии медленных мод переходит в быстрые .и наоборот; это ведет к некоторому выравниванию времен распространения медленных и быстрых мод — в итоге дисперсия уменьшается. Математическое описание явления в общем виде «очень сложное, важнейший результат смешения мод состоит в •следующем:
где
— характеристическое расстояние, на котором устанавливается постоянный модовый состав. Дисперсионное размытие светового импульса «набегает» не пропорционально длине световода L, а пропорционально
т. е. значительно слабее. Величина L0 может быть определена лишь экспериментально, она тем больше, чем совершеннее световод, и может достигать десятков километров. Естественно, что при 
сохраняется прежний закон:
Похожие работы
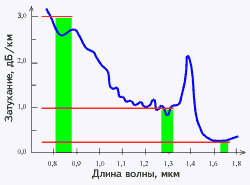
... Оба типа волокна характеризуются двумя важнейшими параметрами: затуханием и дисперсией. Затухание обычно измеряется в дБ/км и определяется потерями на поглощение и на рассеяние излучения в оптическом волокне. Потери на поглощение зависят от чистоты материала, а на рассеяние – от неоднородностей показателя преломления материала. Рис.3 Другой важнейший параметр оптического ...
... большое количество способов компенсации дисперсии. Их можно разделить на следующие три класса [7]: - способы компенсации дисперсии, основанные на управлении пространственным распределением дисперсии волоконно-оптической линии связи (ВОЛС) для обеспечения нулевого суммарного (интегрального) значения дисперсии для всей линии; - способы компенсации дисперсии, основанные на управлении ...
... большие габариты, малый КПД, потребность во внешнем устройстве накачки являются основными причинами, по которым этот источник не используется в современных ВОСП. Практически во всех волоконно-оптических системах передачи, рассчитанных на широкое применение, в качестве источников излучения сейчас используются полупроводниковые светоизлучающие диоды и лазеры. Для них характерны в первую очередь ...
... быть рассчитаны по формулам: Годовая прибыль при запланированном уровне рентабельности составит: 8. Мероприятия по охране труда В данном дипломном проекте требуется разработать передающее устройство одноволоконной оптической системы передачи, рассчитанной на работу с длиной волны 0.85 мкм, которая относится к ближнему инфракрасному диапазону излучения. Поскольку передающее устройство ...
0 комментариев