Навигация
Лінійна задача оптимальної швидкодії
3. Лінійна задача оптимальної швидкодії
Розглянемо лінійну задачу оптимальної швидкодії:
![]() ,
, ![]() , (12)
, (12)
де ![]() ,
, ![]() ,
,
![]() ,
, ![]() – числові матриці розмірності
– числові матриці розмірності ![]() та
та ![]() відповідно.
відповідно.
Область керування задачі ![]() – замкнутий обмежений багатогранник в
– замкнутий обмежений багатогранник в ![]() :
:
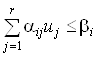 ,
, ![]() , (13)
, (13)
Якщо для будь-якого вектора ![]() , паралельного будь-якому ребру багатогранника
, паралельного будь-якому ребру багатогранника ![]() , система векторів
, система векторів ![]() ,
, ![]() , …,
, …, ![]() (14) є лінійно незалежною, то багатогранник
(14) є лінійно незалежною, то багатогранник ![]() задовольняє умові спільності положення відносно системи (14).
задовольняє умові спільності положення відносно системи (14).
Для перевірки лінійної незалежності векторів (13) достатньо перевірити, чи матриця, стовпцями якої є стовпці (12), є невиродженою, тобто
![]() .
.
Перепишемо формулу (10):
![]() ,
, ![]() ,
,
де ![]() ,
, ![]() –
– ![]() -і рядки матриць
-і рядки матриць ![]() і
і ![]() .
.
Функція Понтрягіна лінійної задачі оптимальної швидкодії має вигляд:
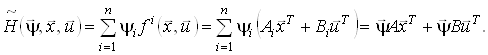 (15)
(15)
Оскільки перший доданок у формулі (15) не залежить від ![]() , то функція
, то функція ![]() досягає максимуму за змінною
досягає максимуму за змінною ![]() одночасно з функцією
одночасно з функцією
![]() .
.
Спряжена система у цьому випадку може бути записана у вигляді:
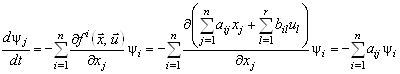 ,
, ![]() ,
,
або у векторній формі
![]() . (16)
. (16)
Позначимо через ![]() . З теореми 2 випливає, що якщо
. З теореми 2 випливає, що якщо ![]() – оптимальне керування, то існує такий ненульовий розв’язок
– оптимальне керування, то існує такий ненульовий розв’язок ![]() системи (16), для якого в кожний момент часу функція
системи (16), для якого в кожний момент часу функція ![]() набуватиме максимального значення за змінною
набуватиме максимального значення за змінною ![]() :
:
![]() . (17)
. (17)
Оскільки система (17) з постійними коефіцієнтами не містить невідомих функцій ![]() і
і ![]() , то всі її розв’язки можна легко знайти, після чого, використовуючи їх для розв’язання задачі максимізації функції
, то всі її розв’язки можна легко знайти, після чого, використовуючи їх для розв’язання задачі максимізації функції ![]() на множині
на множині ![]() , знаходимо оптимальні керування
, знаходимо оптимальні керування ![]() .
.
Для будь-якого нетривіального розв’язання ![]() системи (11) співвідношення (14) однозначно визначає керування
системи (11) співвідношення (14) однозначно визначає керування ![]() , причому це керування кусково стале, а значеннями керування в точках неперервності є вершини багатогранника
, причому це керування кусково стале, а значеннями керування в точках неперервності є вершини багатогранника ![]() .
.
Точки розриву оптимальної функції керування ![]() відповідають зміні значення керування і називаються точками перемикання. Якщо
відповідають зміні значення керування і називаються точками перемикання. Якщо ![]() – точка перемикання, то ліворуч від неї керування має одне значення, наприклад,
– точка перемикання, то ліворуч від неї керування має одне значення, наприклад, ![]() , а праворуч інше –
, а праворуч інше – ![]() .
.
Позначимо через ![]() підмножину у
підмножину у ![]() виду
виду
![]() . (18)
. (18)
Якщо всі корені характеристичного рівняння матриці ![]() з (14) є дійсними, то для будь-якого розв’язання
з (14) є дійсними, то для будь-якого розв’язання ![]() рівняння (18) кожна з функцій
рівняння (18) кожна з функцій ![]() є кусково сталою і має не більше ніж
є кусково сталою і має не більше ніж ![]() перемикань (
перемикань (![]() – порядок системи (16)).
– порядок системи (16)).
Керування ![]() називається екстремальним керуванням, якщо воно задовольняє принципу максимуму.
називається екстремальним керуванням, якщо воно задовольняє принципу максимуму.
Для лінійної задачі оптимальної швидкодії з областю керування – багатогранником ![]() керування
керування ![]() є екстремальним, якщо існує таке нетривіальне розв’язання
є екстремальним, якщо існує таке нетривіальне розв’язання ![]() системи (17), для якого матиме місце співвідношення (18).
системи (17), для якого матиме місце співвідношення (18).
Зрозуміло, що будь-яке оптимальне керування є екстремальним. Тому, щоб знайти оптимальне керування, що переводить фазову точку зі стану ![]() у стан
у стан ![]() , треба відшукати всі екстремальні керування з цими крайовими умовами, а потім серед них вибрати те, що здійснює перехід за найменший час.
, треба відшукати всі екстремальні керування з цими крайовими умовами, а потім серед них вибрати те, що здійснює перехід за найменший час.
У загальному випадку можуть існувати кілька оптимальних керувань, що переводять фазову точку зі стану ![]() у стан
у стан ![]() , але якщо початок координат у просторі керувань є внутрішньою точкою багатогранника
, але якщо початок координат у просторі керувань є внутрішньою точкою багатогранника ![]() , то екстремальне керування єдине. Отже, у лінійних задачах оптимальної швидкодії принцип максимуму дозволяє не тільки визначити вид оптимальних керувань, але й одержати умови єдиності оптимального керування.
, то екстремальне керування єдине. Отже, у лінійних задачах оптимальної швидкодії принцип максимуму дозволяє не тільки визначити вид оптимальних керувань, але й одержати умови єдиності оптимального керування.
Припустимо, що початок координат є внутрішньою точкою багатогранника ![]() припустимих керувань. Якщо
припустимих керувань. Якщо ![]() і
і ![]() – два екстремальних керування, що переводять фазову точку зі стану
– два екстремальних керування, що переводять фазову точку зі стану ![]() у стан
у стан ![]() за час
за час ![]() і
і ![]() відповідно, то
відповідно, то ![]() і
і ![]() ,
, ![]() .
.
У теоремі має місце умова ![]() .
.
Теорема. Якщо існує хоча б одне керування, що переводить систему (17) зі стану ![]() у стан
у стан ![]() , то існує й оптимальне по швидкодії керування, що також переводить систему з
, то існує й оптимальне по швидкодії керування, що також переводить систему з ![]() у
у ![]() .
.
Похожие работы
... ідно вдосконалювати матеріальне й соціальне стимулювання працівників. Одним з напрямків удосконалювання системи стимулювання праці у АТ «Цукровий комбінат» є реалізація вартісної концепції оплати праці на рівні підприємства припускає зміну системи внутріфірмового керування й стимулювання на основі розвитку внутрівиробничих товарно-грошових відносин між структурними одиницями підприємства аж до ...
... випадків, аварій, а з цим і простоїв на підприємстві, укріпити та створити культуру трудової діяльності. Виконання та розробка дипломного проекту “ Розробка дослідження системи керування електроприводом змінного струму дизель-потягу з використанням нейронних мереж ” відбувається за допомогою комп'ютера, тому питання охорони праці розглядаються щодо забезпечення здорових і безпечних умов роботи ...
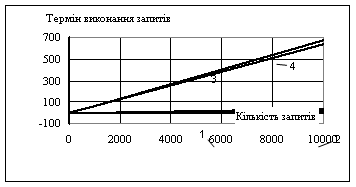
... і Рисунок 6.2 – Графік залежності зони нечутливості від зниження втрат7. Оптимальне керування режимом ЕС в темпі процесу Керування потоками потужності в ЕС виконується за допомогою трансформаторів з РПН. Інформація про стан системи, що включає параметри режиму та регулюючих пристроїв отримується з бази даних оперативного інформаційно-керуючого комплексу (ОІКК). На основі поточної інформац ...
... в даній роботі, була опробована й досліджена в реальних умовах моєї професійної діяльності й показала свою працездатність і ефективність. 3. Розробка системи керування та актуалізації інформації web-сайту національного оператора Енергоринка 3.1 Вибір інструментарію для створення web-сайту та системи керування Перед тим, як безпосередньо перейти до створення Web-сайту Національного ...




0 комментариев