Навигация
Обратное дискретное преобразование Лапласа
Предмет: Теория Автоматического Управления
Тема: Обратное дискретное преобразование Лапласа
1. Обратное дискретное преобразование Лапласа
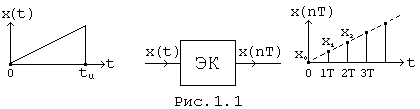
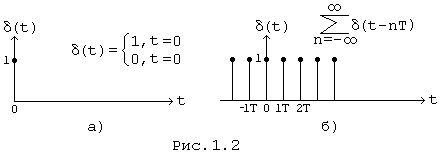
Решетчатая функция – это результат временного квантования непрерывного сигнала – которая представляет значение непрерывного сигнала в дискретные моменты времени. Решетчатая функция получается перемножением непрерывной функции на сигма-функцию. Ее можно определить по ее изображению, используя различные способы:
1. С помощью формул обратного дискретного преобразования Лапласа.
2. С помощью разложения на простые дроби.
3. С помощью разложения в степенной ряд.
В данном реферате мы рассмотрим обратное дискретного преобразование Лапласа.
2. Определение оригинала с помощью формул обратного дискретного преобразования Лапласа
Для непрерывных оригиналов обратное преобразование Лапласа имеет вид:
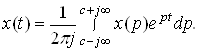 (1)
(1)
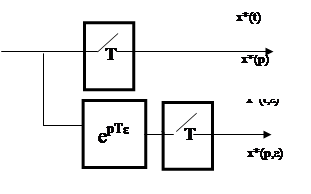
Для нахождения формул обратного дискретного преобразования Лапласа установим связь между плоскостями p и z. Отображение плоскости P в плоскость Z осуществляется с помощью подстановки z = epT.
Так как p = c+jw, то z = epT = ecTe jwT, где ecT- модуль z, а wT- фаза z.
Если с = 0, то
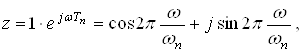
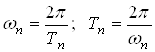 .
.
 z = e pT
z = e pT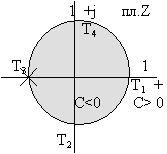
Рис. 1
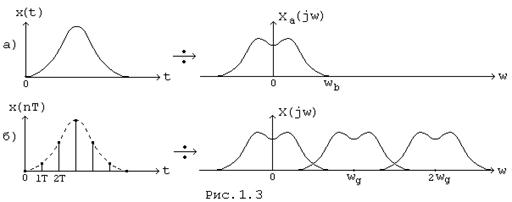
Точки на мнимой оси дискретной плоскости будут повторяться, поэтому на плоскости можно выделить бесконечное множество полос с шириной wп (0.. wп , wп ..2wп и т. д.), которые дают одно и тоже изображение в плоскости Z. Корни в плоскости P являются периодическими, повторяющимися и заключены в любую из полос. Если С > 0, что соответствует правой полуплоскости, то амплитуда z > 1.
Интегрировать можно по частотам расположенным в любой из полос, считая ее как основную, а значения интеграла в других полосах просуммировать. Для удобства интегрирования в качестве основной полосы принимаем полосу частот от -wп /2 до wп/
При переходе в плоскость Z интегрирование осуществляется по замкнутому контуру.
Пример 7. Определить непрерывную функцию, если ее дискретное изображение определяется соотношением
![]()
Решение: Определяем значения полюсов z1 = 1, их количество n = 1 и
кратность m = 1. Используя формулу обратного дискретного преобразования, определяем оригинал

Т. е. заданному изображению соответствует единичная функция.
Пример 8. Определить непрерывную функцию, если дискретное изображение имеет вид
Решение: Определяем значения полюсов z1 = 1, их количество n = 1 и
кратность m =
Определяем оригинал, используя формулу обратного дискретного преобразования
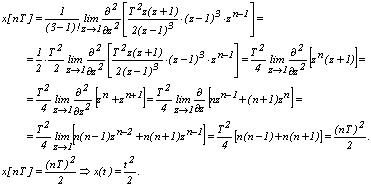
Пример 9. Определить непрерывную функцию, если дискретное изображение имеет вид
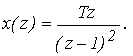
Решение: Определяем значения полюсов z1 = 1, их количество n = 1 и кратность m = Используя формулу обратного дискретного преобразования, определяем оригинал
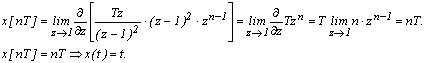
Пример 10. Определить непрерывную функцию, если ее дискретное изображение равно
![]()
Решение: Определяем значения полюсов z1 = d, их количество n = 1 и
кратность m = 1. Используя формулу обратного дискретного преобразования, определяем оригинал

Пример 11. Определить непрерывную функцию, если ее дискретное изображение равно
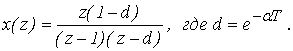
Решение: Определяем значения полюсов z1 = 1, z2 = d, их количество
n = 2 и кратность m = 1. Используя формулу обратного дискретного преобразования, определяем оригинал

Пример 1 Определить непрерывную функцию, если ее дискретное изображение равно
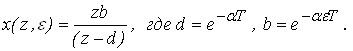
Решение: Определяем значения полюсов z1 = d их количество n = 1 и кратность m = 1. Используя формулу обратного дискретного преобразования, определяем оригинал
![]()
Похожие работы
... На основании теоремы Коши о вычетах этот интеграл можно определить как сумму вычетов по полюсам подынтегральной функции. (8) Это третья формула прямого дискретного преобразования Лапласа. Пример 3. Определить дискретное преобразование Лапласа для еди-ничной функции. Решение: Функции x (t) = 1 (t) соответствует изображение Записываем характеристическое уравнение и определяем значения ...
... . Эквивалентная флюктуационная составляющая отличается от флюктуационной составляющей непрерывной системы. Ее дисперсия равна . Таким образом, в дискретной системе закон изменения параметров определяется только периодом повторения импульсов. Математическое описание дискретных систем Z-преобразование и его свойства Для описания и анализа дискретных систем используется соответствующий ...
... . В результате, на выходе реле сигнал будет непрерывным, но ступенчатым 3.2.2.3 Релейно-импульсные системы В них происходит квантование сигналов по времени и по уровню. К этому типу относятся цифровые системы управления, в частности АСУТП с используемым ВК. При большом количестве разрядов АЦП и ЦАП квантованием можно пренебречь, и отнести такие системы к импульсным. 3.2.2.4 Системы на ...
... номерами можно пренебречь ввиду их малости, что не окажет заметного влияния на спектр сигнала. Пример. Осуществить дискретизацию экспоненциального импульса X(t) = Ae-at = 1 e-10t и сравнить спектры исходного и дискретного сигналов. Решение. График сигнала X(t) представлен на Рис. 1.8 Пусть T = 0,02с. В этом случае плавным соединением отсчетов сигнала (штриховая линия на Рис. 1.8) сигнал ...
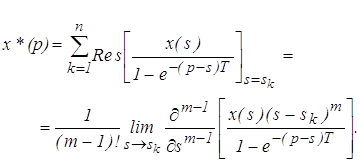
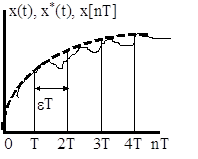
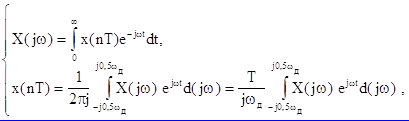
0 комментариев