Навигация
2. Типы сигналов
2.1 Аналоговый сигнал
 <>
<>
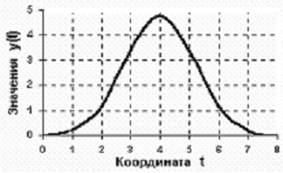
Рисунок 5. Аналоговый сигнал.
Аналоговый сигнал (analog signal) является непрерывной функцией непрерывного аргумента, т.е. определен для любого значения аргументов. Источниками аналоговых сигналов, как правило, являются физические процессы и явления, непрерывные в динамике своего развития во времени, в пространстве или по любой другой независимой переменной, при этом регистрируемый сигнал подобен (“аналогичен”) порождающему его процессу. Пример математической записи сигнала: y(t) = 4.8 exp[-(t-4)2/2.8]. Пример графического отображения данного сигнала приведен на рисунке 5, при этом как сама функция, так и ее аргументы, могут принимать любые значения в пределах некоторых интервалов y1 Δ y Δ y2, t1 Δ t Δ t2. Если интервалы значений сигнала или его независимых переменных не ограничиваются, то по умолчанию они принимаются равными от - Δ до + Δ. Множество возможных значений сигнала образует континуум - непрерывное пространство, в котором любая сигнальная точка может быть определена с точностью до бесконечности. Примеры сигналов, аналоговых по своей природе - изменение напряженности электрического, магнитного, электромагнитного поля во времени и в пространстве.
2.2 Дискретный сигнал
 <>
<>
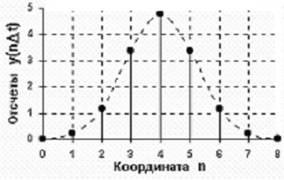
Рисунок 6. Дискретный сигнал.
Дискретный сигнал Δdiscrete signal) по своим значениям также является непрерывной функцией, но определенной только по дискретным значениям аргумента. По множеству своих значений он является конечным Δсчетным) и описывается дискретной последовательностью отсчетов Δsamples) yΔnΔt), где y1 Δ y Δ y2, Δt - интервал между отсчетами Δинтервал или шаг дискретизации, sample time), n = 0,1,2,...,N. Величина, обратная шагу дискретизации: f = 1/Δt, называется частотой дискретизации Δsampling frequency). Если дискретный сигнал получен дискретизацией Δsampling) аналогового сигнала, то он представляет собой последовательность отсчетов, значения которых в точности равны значениям исходного сигнала по координатам nΔt.
Пример дискретизации аналогового сигнала, приведенного на рисунке 5, представлен на рисунке 6. При Δt = const Δравномерная дискретизация данных) дискретный сигнал можно описывать сокращенным обозначением yΔn) или y[t]. При неравномерной дискретизации сигнала обозначения дискретных последовательностей обычно заключаются в фигурные скобки - {sΔti)}, а значения отсчетов приводятся в виде таблиц с указанием значений координат ti. Для числовых последовательностей Δравномерных и неравномерных) применяется и следующее числовое описание:
sΔti) = {a1,a2, ..., aN}, t = t1,t2, ...,tN.
2.3 Цифровой сигнал
 <>
<>
Рисунок 7. Цифровой сигнал.
Цифровой сигнал Δdigital signal) квантован по своим значениям и дискретен по аргументу. Он описывается квантованной решетчатой функцией yn = Qk[yΔnΔt)], где Qk - функция квантования с числом уровней квантования k, при этом интервалы квантования могут быть как с равномерным распределением, так и с неравномерным, например - логарифмическим. Задается цифровой сигнал, как правило, в виде дискретного ряда числовых данных - числового массива по последовательным значениям аргумента при Δt = const, но в общем случае сигнал может задаваться и в виде таблицы для произвольных значений аргумента.
По существу, цифровой сигнал по своим значениям Δотсчетам) является формализованной разновидностью дискретного сигнала при округлении отсчетов последнего до определенного количества цифр, как это показано на рисунке 7. Цифровой сигнал конечен по множеству своих значений. Процесс преобразования бесконечных по значениям аналоговых отсчетов в конечное число цифровых значений называется квантованием по уровню, а возникающие при квантовании ошибки округления отсчетов Δотбрасываемые значения) – шумами Δnoise) или ошибками Δerror) квантования.
В дискретных системах и в ЭВМ сигнал всегда представлен с точностью до определенного количества разрядов, а, следовательно, всегда является цифровым. С учетом этих факторов при описании цифровых сигналов функция квантования обычно опускается Δподразумевается равномерной по умолчанию), а для описания сигналов используются правила описания дискретных сигналов. Что касается формы обращения цифровых сигналов в системах хранения, передачи и обработки, то, как правило, они представляет собой комбинации коротких одно- или двуполярных импульсов одинаковой амплитуды, которыми в двоичном коде с определенным количеством числовых разрядов кодируются числовые последовательности сигналов Δмассивов данных).
 <>
<>
Рисунок 8. Дискретно-аналоговый сигнал.
В принципе, квантованными по своим значениям могут быть и аналоговые сигналы, зарегистрированные соответствующей аппаратурой Δрисунок 8), которые принято называть дискретно-аналоговыми. Но выделять эти сигналы в отдельный тип не имеет смысла - они остаются аналоговыми кусочно-непрерывными сигналами с шагом квантования, который определяется допустимой погрешностью измерений.
Похожие работы
... . 29: 223-246. Павлинов И.Я. (1995): Классификация как гипотеза: вхождение в проблему. - Ж. общ. биол. 56 (4): 411-424. Панов Е.Н. (1978): Механизмы коммуникации у птиц. М.: Наука. 1-303. Панов Е.Н. (1983а): Методологические проблемы в изучении коммуникации и социального поведения животных. - Итоги науки и техники. Зоол. позв. М.: ВИНИТИ. 12: 5-70. Панов Е.Н. (1983б): Эмпирический факт и его ...
... источника. Разумеется, для правильного выбора кода надо знать информационные характеристики источника сообщений и характеристики используемого канала связи. Физические характеристики канала и сигнала. Обычно телемеханические сигналы передаются посылками электрического тока по проводным линиям связи, но иногда используется и радиоканал. В обоих случаях перенос электромагнитной энергии сигналов ...
... сигналов. 1. ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ. 1.1. Вводные замечания. В предисловии дано обоснование направленности содержания курсовой работы с учетом места курса "Радиотехнические цепи и сигналы" в подготовке радиоинженеров. Задание учитывает устойчивые тенденции перехода от аналоговых систем к цифровым системам передачи и обработки непрерывных сообщений на основе дискретизации, ...
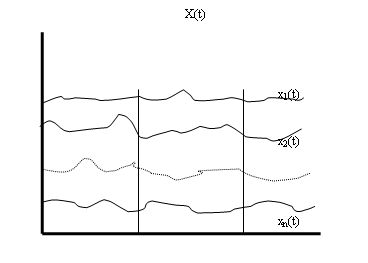
... функции Rx (t) и энергетического спектра (спектральной плотности) случайного процесса Sx (w), которые связанны преобразованием Фурье или формулами Винера - Хинчина ; (11) . (12) 5. Геометрическое представление сигналов и их характеристик Любые n - чисел можно представить в виде точки (вектора) в n -мерном пространстве, удаленной от начала координат на расстоянии D, где . (13) ...


0 комментариев