Навигация
Определение параметров катушки индуктивности методом амперметра, вольтметра и ваттметра при питании напряжением частоты 50 Гц
1. Определение параметров катушки индуктивности методом амперметра, вольтметра и ваттметра при питании напряжением частоты 50 Гц.
2. Исследование электрической цепи с последовательным соединением резистора, катушки индуктивности и конденсатора при различных соотношениях индуктивного и емкостного сопротивлений.
Описание лабораторной установки
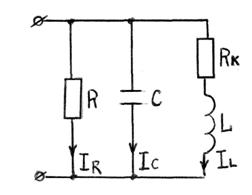
Схема экспериментальной установки для исследования электрической цепи с последовательным соединением элементов R, L, C представлена на рис. 6.
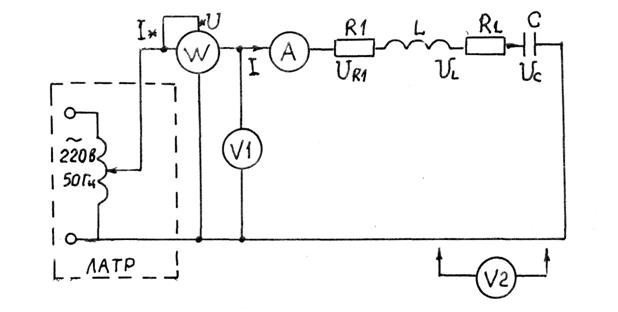
Рис. 6
В её состав входят ЛАТР (лабораторный автотрансформатор), на выходных клеммах которого устанавливается напряжение U = 40 В.
Вольтметр V1 предназначен для измерения действующего значения напряжения, прикладываемого к электрической цепи; соответственно измеряет действующие значения напряжения на элементах R, L, C.
Амперметр А измеряет действующее значение тока в цепи. В качестве R1 используется реостат (Rреост = 30 Ом, 5 А), емкости С – магазин емкостей
(С = 1 мкФ ÷ 20 мкФ), индуктивности L – катушка индуктивности (с параметрами L и RL, определяемыми экспериментально).
Цель работы – исследование электрической цепи с параллельным соединением элементов R, L, C при различных соотношениях индуктивного и емкостного сопротивлений.
Общие сведения
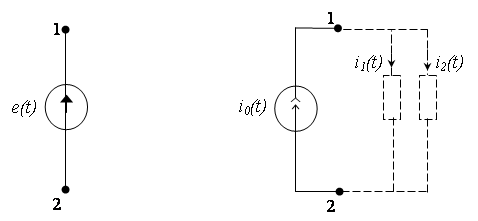
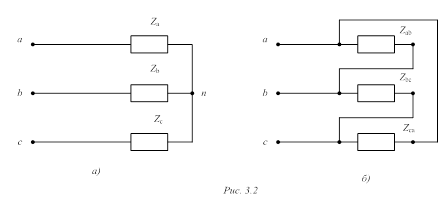
При параллельном соединении элементов R, L, C (рис. 1) полная проводимость равна ![]() (1)
(1)
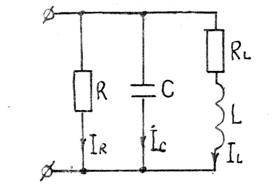
где g = 1/R – активная проводимость цепи;
b – реактивная проводимость цепи.
Реактивная проводимость цепи при этом определяется выражением ![]() (2)
(2)
Рис. 1
Ток в цепи определяется выражением
![]() (3)
(3)
Ток в активной проводимости совпадает с напряжением по фазе
![]() (4)
(4)
Ток в ёмкости определяет напряжение по фазе на 900
![]() (5)
(5)
Ток в индуктивности отстаёт от напряжения по фазе на 900
![]() (6)
(6)
Средняя активность мощность, расходуемая в цепи
![]() (7)
(7)
Сдвиг фаз между напряжением U на зажимах цепи и током I в ней определяется выражениями
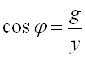 (8)
(8)
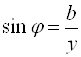 (9)
(9)
Векторная диаграмма напряжения и токов в цепи показана на рис. 2 (при bC > bL).
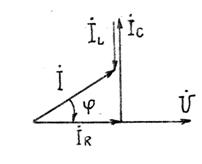 Резонансом токов называется такое состояние электрической цепи при параллельном включении элементов R, L, C, когда сдвиг по фазе между напряжением на зажимах цепи и током в ней равны нулю, при этом bC = bL, а ток в неразветвлённой цепи имеет наименьшее значение.
Резонансом токов называется такое состояние электрической цепи при параллельном включении элементов R, L, C, когда сдвиг по фазе между напряжением на зажимах цепи и током в ней равны нулю, при этом bC = bL, а ток в неразветвлённой цепи имеет наименьшее значение.
При постоянных значениях L и C резонансная частота определяется выражением
Рис. 2
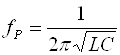 (11)
(11)
Резонансное значение тока в цепи
![]() (12)
(12)
Ток в активной проводимости при резонансе равен полному току
![]() (13)
(13)
Токи в ёмкости и индуктивности при резонансе равны между собой
![]() (14)
(14)
где ![]() - добротность контура;
- добротность контура;
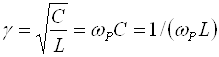 - волновая и характеристическая проводимость контура.
- волновая и характеристическая проводимость контура.
Средняя мощность при резонансе
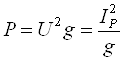 (15)
(15)
Векторная диаграмма напряжения и токов при резонансе токов показана на рис. 3.
Настроить цепь в резонанс с частотой источника питания можно изменением индуктивности или ёмкости, а также с помощью изменения частоты источника питания.
Графики изменений токов цепи, сдвига фаз и напряжения на зажимах цепи при изменении частоты источника питания называются частотными характеристиками контура и показаны на рис. 4.
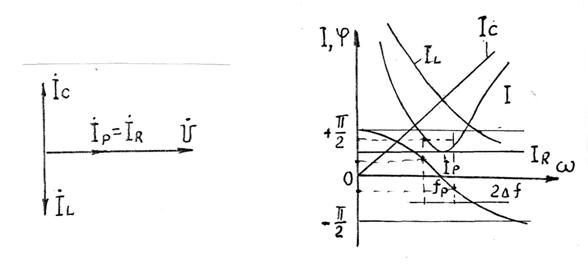
Рис. 3 Рис. 4
Частотные характеристики контура могут быть построены по уравнениям (3), (4), (5), (8), (9), (10).
Частотная характеристика тока позволяет определить экспериментально добротность контура
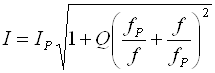 (16)
(16)
Если определить полосу пропускания частот ![]() , пропускаемых контуром на уровне
, пропускаемых контуром на уровне ![]() , то добротность контура можно найти из выражения
, то добротность контура можно найти из выражения
![]() (17)
(17)
На границе полосы пропускания сдвиг фаз между напряжением на зажимах цепи и током в ней составляет φ = ± 450. Если катушка индуктивности L имеет собственное активное сопротивление (рис. 5), то ток в ней определяется выражением
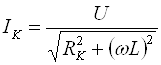 (18)
(18)
 Вычислив эквивалентные проводимости катушки
Вычислив эквивалентные проводимости катушки
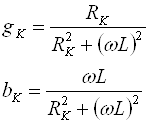 (19)
(19)
Рис. 5
перейдём к эквивалентной схеме с параллельным соединением R, L, C.
Полная активная проводимость эквивалентного параллельного контура равна сумме внешней проводимости ![]() и собственной активной проводимости gK катушки L
и собственной активной проводимости gK катушки L
![]() (20)
(20)
Эквивалентная индуктивность такого контура
![]() (21)
(21)
Резонансная частота контура будет зависеть от собственного сопротивления RK катушки L
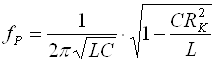 (22)
(22)
При относительно малом сопротивлении катушки RK >> ωL можно пользоваться выражениями (11) – (17).
Содержание работы
Исследование электрической цепи с параллельным соединением резистора, катушки индуктивности и конденсатора при различных соотношениях индуктивного и ёмкостного сопротивлений.
Описание лабораторной установки
Схема экспериментальной установки для исследования электрической цепи с параллельным соединением элементов R, L, C представлена на рис. 6.
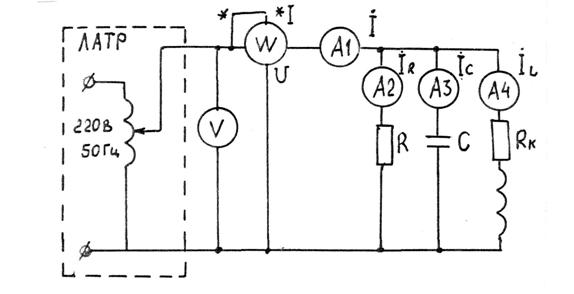
Рис. 6
В её состав входят ЛАТР (лабораторный автотрансформатор), на входных клеммах которого устанавливают напряжение U = 20 В.
Вольтметр V предназначен для измерения действующего значения напряжения, прикладываемого к электрической цепи. Амперметр А1 измеряет действующее значение тока в неразветвлённой части цепи, амперметры А2, А3, А4 измеряют действующие значения токов соответственно в резисторе (А2), конденсаторе (А3), катушке индуктивности (А4). В качестве резисторной нагрузки используется реостат (R1 = 300 Ом, 0,5 А), ёмкости С – магазин конденсаторов (С = 1 Мкф ÷ 20 Мкф), индуктивность L – катушка индуктивности (L = 50 мГн, RK = 30 Ом).
Информационно-методическое обеспечение дисциплины:
Нейман Л.Р., Дениргян К.С. ТОЭ. Т1, Т2. - М.: Высшая школа, 1981. Бессанов Л.А. ТОЭ. Т1, Т2, Т3. - М.: Высшая школа, 1984. Ионкин П.А. и др. ТОЭ. Т1. - М.: Высшая школа 1981. Основы теории цепей /Г.В. Зевенс, П.А. Ионкин, А.В. Нетушин, С.В. Страхов/ М.: Высшая школа, 1989. Матхомов П.Н. Основы анализа электрических цепей. Линейные цепи. – М.: Высшая школа, 1990. Матхамов П.Н. Основы анализа электрических цепей. Нелинейные цепи. – М.: Высшая школа, 1990. Сборник задач и упражнений по ТОЭ под ред. П.А. Ионкина. – М.: Энергоиздат, 1982. Шебес М.Р. Задачник по теории линейных электрических цепей. – М.: Высшая школа, 1989. Задачник по ТОЭ– М.: Энергия, 1975.
Похожие работы
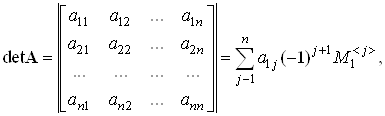
... – матрица проводимостей, обратная матрице сопротивлений ветвей. Если в функции fk и jk входят производные токов и напряжений, то процессы в этой линейной или нелинейной электрической цепи будут характеризоваться системой, соответственно, линейных или нелинейных дифференциальных уравнений. При отсутствии производных в функциях fk и jk процессы в этой линейной или нелинейной электрической цепи ...
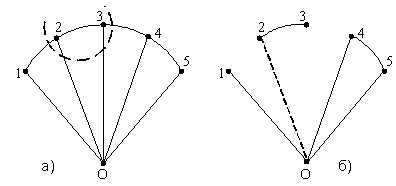
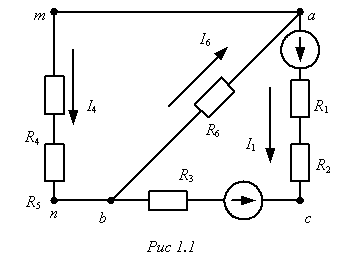
... любой из ветвей выбранного сечения приводит к связному графу. Отмеченные выше понятия и положения будут использованы в дальнейшем при расчете электрических цепей по методам, вытекающим из законов Кирхгофа. Теорема замещения В теории электрических цепей как при доказательствах ряда ее положений, так и при численных расчетах используется теорема замещения: значения всех напряжений и токов в ...
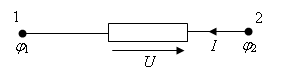
... . 1.2. Если в данный момент времени , это означает, что направление тока в проводнике совпадает с направлением, указанным стрелкой, т. е. положительные заряды перемещаются в направлении стрелки. В теории электрических цепей допускается возможность однозначной, не зависящей от выбора пути, оценки электрических напряжений меду любыми двумя зажимами исследуемой электрической цепи. Это позволяет ...
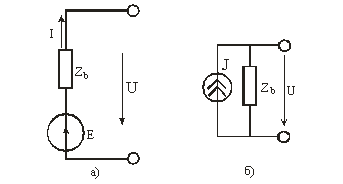
чает в себя источники мощности (активные элементы) и приемники (пассивные элементы). В качестве пассивного линейного элемента в цепях постоянного тока выступает резистор, имеющий электрическое сопротивление R. Единица измерения Ом. Величина, обратная сопротивлению, называется электрической проводимостью: G = 1/R. Единица измерения См - сименс. В качестве активных элементов - источников ...





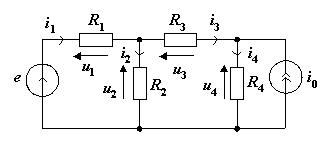



0 комментариев