Навигация
1. Стационарная передача через плоскую стенку
Теплота дымовых газов передаётся через стенку воде. Принимая температуру газов tж1, воды tж2, коэффициент теплоотдачи газами стенки α1 и от стенки воде α2 и считая стенку плоской, требуется:
1. Подсчитать термические сопротивления, коэффициенты теплопередачи и количество передаваемой теплоты от газов к воде через 1м2 стенки для следующих случаев:
а) стенка стальная совершенно чистая, толщиной δ2 (λ2=50 Вт/(м·ºС);
б) стенка стальная, со стороны воды покрыта слоем накипи толщиной δ3 (λ3=2 Вт/(м·ºС);
в) стенка стальная, со стороны газов покрыта слоем сажи толщиной δ1=2 мм(λ1=0,2 Вт/(м·ºС);
г) стенка стальная, со стороны воды покрыта слоем накипи толщиной δ3, а со стороны газов – сажей толщиной δ1.
2. Определить температуры всех слоев стенки для случая г.
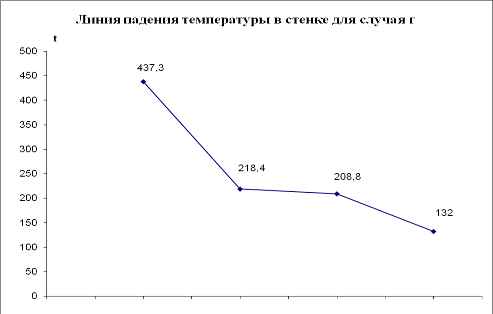
3. Построить в масштабе линию падения температуры в стенке для случая г.
Дано: tж1=950ºС, tж2=210ºС, α1=65 Вт/(м2·ºС), α2·10-3=2,1 Вт/(м2·ºС), δ2=19 мм, δ3=5 мм.
Термическое сопротивление теплопередаче:
![]()
![]()
![]()
![]()
Коэффициенты теплопередачи
![]()
![]()
![]()
![]()
Количество передаваемой теплоты от газов к воде через 1 м2 стенки определим из уравнения теплопередачи:
![]()
![]()
![]()
![]()
![]()
Температуры всех слоев стенки для случая г.
Плотность теплового потока от газов к стенке
![]()
отсюда ![]()
Плотность теплового пока через слой сажи
![]()
Отсюда ![]()
Плотность теплового потока через стальную стенку
![]()
Отсюда ![]()
Плотность теплового потока через слой накипи
![]()
Отсюда ![]()
2. Расчет тепловой изоляции
Стальная труба (λтр) внутренним диаметром d с толщиной стенки δ1 покрыта слоем изоляции, коэффициент теплопроводности которой λиз. По трубе протекает вода, температура которой tж1. Коэффициент теплоотдачи воды к стенке α1. Снаружи труба омывается свободным потоком воздуха, температура которого tж2=20ºС; коэффициент теплоотдачи к воздуху α2 =10 Вт/(м2·ºС);
Требуется:
1. Найти толщину изоляционного материала, обеспечивающую температуру наружной поверхности изоляции 60ºС.
2. Сопоставить тепловые потоки через трубу с изоляцией и без неё при тех же tж1, tж2,α1 и α2.
3. Дано: d=66 мм; tж1=250°С; α110-3=1,7 Вт/(м2°С); λиз=0,08 Вт/(м2°С); λтр=48Вт/(м2°С).
Линейная плотность теплового потока через изолированную трубу

Линейная плотность теплового потока от изоляции к наружному воздуху
![]()
Приравниваем правые части этих уравнений и представим решение в виде
![]()
Где
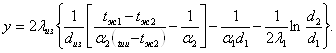
Подставим значение соответствующих величин и получим
![]()
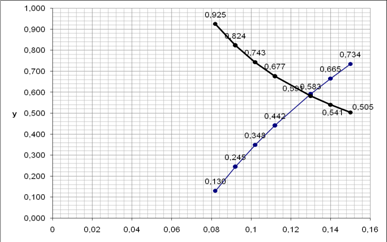
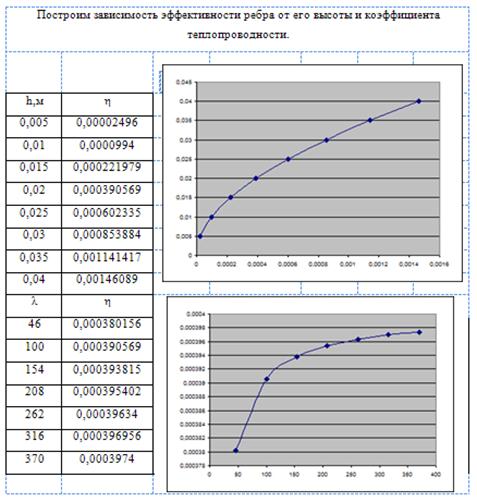
Для графического решения полученного уравнения зададимся значениями dиз, определим y и ![]() , а полученные результаты представим в таблице:
, а полученные результаты представим в таблице:
| dиз | 0,082 | 0,092 | 0,102 | 0,112 | 0,122 | 0,132 | 0,142 |
| dиз/ d2 | 1,139 | 1,278 | 1,417 | 1,556 | 1,694 | 1,833 | 1,972 |
|
| 0,130 | 0,245 | 0,348 | 0,442 | 0,527 | 0,606 | 0,679 |
| y | 0,925 | 0,824 | 0,743 | 0,677 | 0,621 | 0,574 | 0,533 |
![]()
Полученные данные наносим на график и получаем значение корня dиз=0,129 м, которое удовлетворяет уравнению ![]()
Линейная плотность теплового потока через изолированную трубу

Линейная плотность теплового потока неизолированного трубопровода
 =515,5
=515,5
Следовательно, у неизолированного трубопровода потери теплоты с 1 м в 3,2 раза больше, чем у изолированного.
Похожие работы
... датчика и осциллографа. Экспериментальные кривые зависимости времени τ горения частиц от давления p, соответствуют теоретической зависимости. Представляют интерес экспериментальные исследования процесса горения отдельной угольной частицы, движущейся в потоке газа. Такого рода опыты проводили Н. И. Сыромятников и 3.И.Леонтьева. После воспламенения частицы наблюдалось замедление скорости ее ...
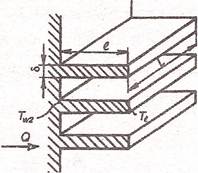
ти, α2 - коэффициент теплоотдачи от оребренной поверхности. Тепловой поток с межреберной поверхности Qм = α2·Ам·(Тw2–Tf2). Тепловой поток с поверхности ребер Qр =α2·Ар·(Тw2 – Tf2)·ψр. Общий тепловой поток с оребренной поверхности Q2,р=α2·(Ам+ψр·Ар)·(Тw2–Tf2), где ψр =Q/Qmax (1). Допускаем, что коэффициент теплоотдачи α2 одинаков для межреберной ...
... ,Sб=pdL, из (2.14) определим временную зависимость толщины оксидной пленки на поверхности проводника: , . (2.15) Дифференциальные уравнения (2.13), (2.14) с учетом уравнений (2.9), (2.5)–(2.12) описывают нестационарный высокотемпературный тепломассообмен и кинетику окисления вольфрамового проводника, нагреваемого электрическим током в газообразной среде, ...
... аппарата будет выглядеть Р 0,6р-0,8-55,8-2К-01-4, его габариты . Вывод Эти простейшие тепловые расчеты двух теплообменных аппаратов одинаковой тепловой производительности показывают, что коэффициент теплопередачи за счет более значительной турбулизации потоков практически в 1,5 раза выше у пластинчатого теплообменника, чем у кожухотрубного. Площадь теплообмена, необходимая для придания



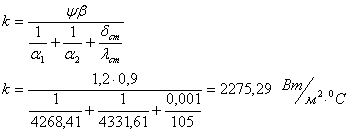
0 комментариев