Навигация
Параметри тунельного ефекту
19635
знаков
0
таблиц
11
изображений
Міністерство освіти і науки України
Прикарпатський національний університет імені Василя Стефаника
Фізико-технічний факультет
Реферат
Параметри тунельного ефекту
м. Івано-Франківськ
2009
1. Тунельний ефект
Розглянемо поведінку частки при проходженні через потенційний бар'єр. Нехай частка, що рухається ліворуч праворуч, зустрічає на своєму шляху потенційний бар'єр висоти U0 і ширини l (мал. 1.1). По класичних виставах рух частки буде таким:
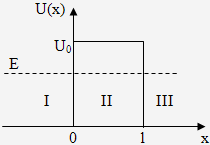
Мал.1.1 Проходження частки через потенційний бар'єр
- якщо енергія частки буде більше висоти бар'єра (E>U0), то частка безперешкодно проходить над бар'єром;
- якщо ж енергія частки буде менше висоти бар'єра (E<U0), то частка відбивається й летить у зворотну сторону;
- крізь бар'єр частка проникнути не може.
Зовсім інакше поведінка частки за законами квантової механіки.
По-перше, навіть при E>U0 є відмінна від нуля ймовірність того, що частка відіб'ється від потенційного бар'єра й полетить назад. По-друге, при E<U0 є імовірність того, що частка проникне « крізь» бар'єр і розміститься в області III. Така поведінка частки описується рівнянням Шредінгера:
. (1.1)
Тут 
- хвильова функція мікрочастинки. Рівняння Шредінгера для області I і III буде однаковим. Тому обмежимося розглядом областей I і II. Отже, рівняння Шредінгера для області I прийме вид:
, (1.2)
увівши позначення:
, (1.4)
остаточно одержимо:
(1.5).
Аналогічно для області II:
, (1.6)
де 
. Таким чином, ми одержали характеристичні рівняння, загальні рішення яких мають вигляд:
при x<0, (1.7)
при x>0 (1.8)
Доданок 
відповідає хвилі, що поширюється в області I у напрямку осі х, А1- амплітуда цієї хвилі. Доданок 
відповідає хвилі, що поширюється в області I у напрямку, протилежному х. Це хвиля, відбита від бар'єра, В1- амплітуда цієї хвилі. Тому що ймовірність знаходження мікрочастинки в тому або іншому місці простору пропорційна квадрату амплітуди хвилі де Бройля, те відношення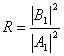 
являє собою коефіцієнт відбиття мікрочастинки від бар'єра.
Доданок 
відповідає хвилі, що поширюється в області II у напрямку х. Квадрат амплітуди цієї хвилі відбиває ймовірність проникнення мікрочастинки в область II. Відношення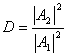 
являє собою коефіцієнт прозорості бар'єра.
Доданок 
повинний відповідати відбитій хвилі, що поширюється в області II. Тому що такої хвилі ні, те В2 слід покласти рівним нулю.
Для бар'єра, висота якого U>E, хвильовий вектор k2 є уявним. Покладемо його рівним ik, де 
є дійсним числом. Тоді хвильові функції 
й 
придбають наступний вид:
(1.9)
(1.10)
Тому що
, те це значить, що є ймовірність проникнення мікрочастинки на деяку глибину в другу область. Ця ймовірність пропорційна квадрату модуля хвильової функції :
. (1.11)
Наявність цієї ймовірності уможливлює проходження мікрочастинок крізь потенційний бар'єр кінцевої товщини l (мал. 1.1). Таке просочування одержало назву тунельного ефекту. По формулі (1.11) коефіцієнт прозорості такого бар'єра буде рівний:
, (1.12)
де D0 – коефіцієнт пропорційності, що залежить від форми бар'єра. Особливістю тунельного ефекту є те, що при тунельнім просочуванні крізь потенційний бар'єр енергія мікрочастинок не міняється: вони залишають бар'єр з тою же енергією, з який у нього входять.
Тунельний ефект відіграє більшу роль в електронних приладах. Він обумовлює протікання таких явищ, як емісія електронів під дією сильного поля, проходження струму через діелектричні плівки, пробій p-n переходу; на його основі створені тунельні діоди, розробляються активні плівкові елементи.
Похожие работы
... НВЧ-коливання - діод Ганна. Ефект Ганна був відкритий у 1963 р американським фізиком Дж. Ганном (J. Gunn) у кристалі арсениду галію з електронною провідністю з прикладеним полем Е ~ (2..3) кВ/см. Ефект Ганна полягає у тому, що при досить великій напрузі, прикладеній до напівпровідника, у цьому напівпровіднику виникають НВЧ-коливання. Цей ефект був ретельно досліджений, з'ясовані фі ...
... та контролю температури; германієві та кремнієві площинні діоди. Теоретичні питання знання, яких необхідне для виконання лабораторної роботи: 1. Фізичні процеси, які відбуваються в результаті контакту напівпровідників з різним типом провідності. 2. Електронно-дірковий перехід у рівноважному стані. Енергетична діаграма. 3. Інжекція та екстракція носіїв заряду. 4. Вольт амперна характеристика ( ...
... , у принципі, здатний обробляти інформацію в 2L/L раз швидше в порівнянні зі своїм класичним аналогом. Звідси відразу видно, що маленькі квантові регістри (L<20) можуть служити лише для демонстрації окремих вузлів і принципів роботи квантового комп’ютера, але не принесуть великої практичної користі, тому що не зуміють обігнати сучасні ЕОМ, а коштувати будуть набагато дорожче. 1.3.Принципи ...
... і ключі реалізовані із зворотними зв’язками на діодах Шоткі. Це дозволило значно підвищити швидкодію схем і є зараз основою надвеликих інтегральних схем, які в свою чергу є базою всієї комп'ютерної електроніки. Окрім цього використовуються елементи емітерно-зв’язної логіки (ЕЗЛ) (на основі диференційних каскадів струмових ключів), n-, p- МОН логіка (на польових транзисторах) та комплементарна ...
0 комментариев